qualunque poligono circoscrittibile e' equivalente ad un triangolo avente come base il perimetro della figura e come altezza il raggio della circonferenza inscritta nella figura
Possiamo considerarlo una conseguenza della nota del teorema precedente
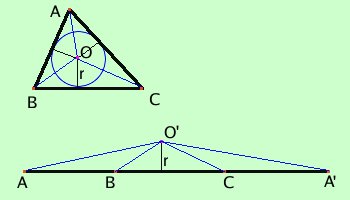
per un accenno di dimostrazione consideriamo un triangolo ABC ed il suo cerchio inscritto di centro O
Per semplicita' prendiamo un triangolo, ma potremmo fare la dimostrazione con un qualunque poligono circoscritto
Il triangolo e' scomponibile nei triangoli ABO, BCO e CAO la cui altezza r e' il raggio del cerchio inscritto
Considero ora il triangolo AA'O in cui il segmento AA' e' congruente al perimetro del triangolo ABC e l'altezza vale r
- Il triangolo ABO' e' equivalente al triangolo ABO perche' la loro base e la loro altezza sono congruenti
- Il triangolo BCO' e' equivalente al triangolo BCO perche' la loro base e la loro altezza sono congruenti
- Il triangolo CA'O' e' equivalente al triangolo CAO perche' la loro base e la loro altezza sono congruenti