Per parlare di queste geometrie occorre andare a modificare il nostro conceto di piano:
Il piano e' uno dei concetti primitivi, e non viene definito proprio perche' ognuno di noi dovrebbe averne il concetto preesistente nella sua mente; tu come l'immagini un piano?
io l'immagino come un pavimento che si espanda da tutte le parti senza avere muri.
Immagina di avere un altezza di 2 metri (cosi' puoi giocare a pallacanestro) e di stare in una stanza a 2 metri dal muro e fai un passo di un metro verso il muro, pero', per magia, ogni volta che fai un passo ti restringi e diventi esattamente la meta'
| passo numero | Ampiezza del passo in cm | Distanza dal muro in cm dopo il passo | 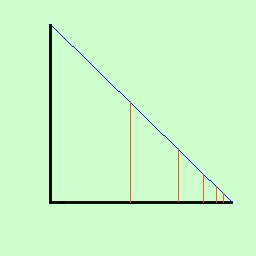 |
| 0 | -- | 200 | |
| 1 | 100 | 100 | |
| 2 | 50 | 50 | |
| 3 | 25 | 25 | |
| 4 | 12,5 | 12,5 |

La figura, che richiama (indegnamente) un disegno di Escher, ti aiuta a capire? Man mano che ti avvicini al bordo c'e' sempre qualcos'altro
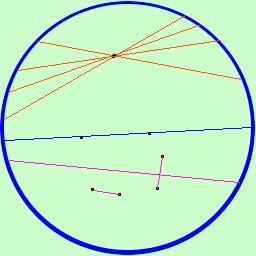
Il piano di Klein e' un piano di questo genere in cui i punti si "addensano" man mano che ti avvicini al bordo; la retta sara' la congiungente due punti sul bordo
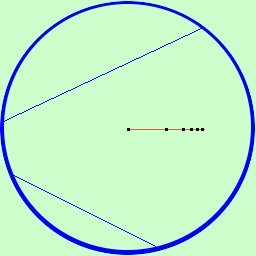
Per un punto passano infinite rette
Per due punti passa una sola retta
La retta divide il piano in due parti tali che prendendo due punti dalla stessa parte il segmento che li unisce non taglia la retta, mentre prendendo due punti da parti opposte il segmento che li unisce taglia la retta