Geometria di Lobacewskij

Geometria di Lobacewskij-Bolyai
Per capire questa geometria dobbiamo prendere un'altra definizione (equivalente) di parallela
Pensa una retta ed un punto fuori di essa, se dal punto traccio una retta obliqua questa incontrera' la prima retta in un punto A, se ora ruoto la retta, fino a farla diventare parallela, il punto si spostera' in B, in C .... , fino all'infinito e le rette saranno parallele quando il punto di incontro e' all'infinito quindi:
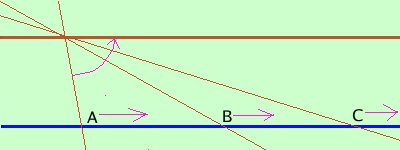
Definizione
due rette sono parallele se hanno in comune un punto allinfinito

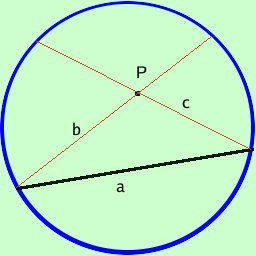
Con questa definizione allora in un piano di Klein da ogni punto fuori della retta si possono tracciare due rette parallele alla retta stessa Le due rette b e c sono parallele alla retta a perche' con essa hanno in comune un punto all'infinito: ricordati che il bordo del cerchio e' l'infinito

In questa geometria per un punto si possono tracciare due rette parallele