L'enunciato stavolta e' gia' nel titolo
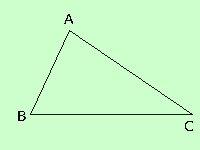Consideriamo un triangolo che abbia il lato AB piu' corto ed il lato AC piu' lungo; dovremo dimostrare che l'angolo BCA^č minore dell'angolo ABC^Per fare l'angolo di fronte ad un lato, ad esempio di fronte ad AB basta che in mezzo alle lettere del lato metti l'altra lettera C, ottieni ABC
| ipotesi | tesi | |
| AC > AB | BCA^< ABC^ |
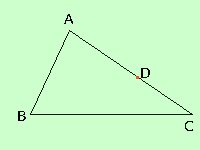Riportiamo sul lato maggiore il lato minore in modo da avere due segmenti congruenti AB = AD
questo ci permette di costruire un triangolo isoscele cogiungendo i punti B e D Infatti il triangolo ABD e' isoscele e quindi ha gli angoli ABD^ e BDA^ congruenti
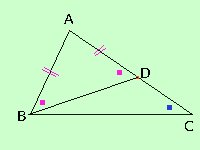
Se ora consideriamo il triangolo BCD l'angolo BDA^ e' esterno mentre l'angolo BCD^ e' interno e non adiacente quindi BDA^ > BCD^
Raccogliendo
ABC^> ABD^= BDA^> BCA^
Per la proprieta' transitiva segue ABC^> BCA^
o, leggendo alla rovescia
BCA^< ABC^
come volevamo
