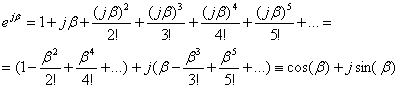Il regime sinusoidale
Una tensione o una
corrente si dice sinusoidale quando la sua ampiezza al variare del tempo è pari
a:
Le precedenti
rappresentano tre espressioni diverse per scrivere la medesima funzione.
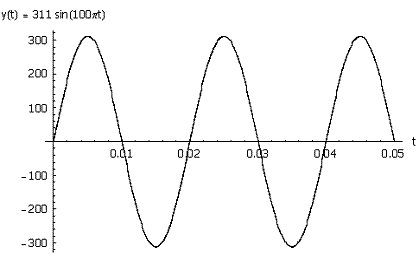
La tensione
disponibile negli appartamenti, ad esempio, è una tensione sinusoidale, come rappresentato
in figura seguente:
|
|
|
Sull’asse delle ascisse si rappresenta il tempo (in secondi), mentre
sull'asse verticale, delle ordinate, si ha y(t), cioè il valore della tensione
all'istante considerato t. In pratica, il valore della tensione, in un periodo,
parte da uno zero e torna al secondo zero successivo, oppure parte dal valore
massimo positivo e finisce al successivo valore massimo positivo, e così via. La
funzione si ripete tale e quale dopo un tempo T detto appunto periodo. Si dice,
quindi, periodo il tempo impiegato da una funzione per ripetersi tale e quale. Matematicamente,
una grandezza si dice periodica se vale:
Si dice frequenza di una funzione sinusoidale il numero di periodi che
compie in un secondo, si indica con la lettera f e si misura in Hz (Hertz). Ad
esempio, f = 50Hz vuol dire che in un secondo l'onda si ripete tale e quale 50
volte, cioè compie 50 periodi o cicli al secondo. Tra periodo e frequenza
esiste la seguente relazione:
La frequenza è l'inverso del periodo. La frequenza della tensione nelle
abitazioni civili è f = 50Hz.
Una sinusoide è la
proiezione di un moto circolare uniforme sull’asse verticale di un “segmento” (vettore)
di lunghezza unitaria, con origine nel centro degli assi cartesiani, che ruota
in senso antiorario. Una cosinusoide, invece, è la proiezione del moto
sull’asse orizzontale. Per fissare le idee, se colleghiamo le spazzole di un
alternatore agli estremi di un filo conduttore di data resistenza, nel filo
stesso circola una corrente sinusoidale. L’unica differenza nella forma d’onda
di sinusoide e cosinusoide è uno sfasamento reciproco pari a 
/ 2 e spesso useremo il termine “sinusoidale” per indicare
entrambe le funzioni.
Si definisce
pulsazione (o velocità angolare) la grandezza 
calcolata come segue:
Si misura in
radianti al secondo ed il suo significato si evince direttamente dalla sua
definizione, ovvero esprime la velocità angolare (“quale angolo percorre il
vettore in un secondo”) del vettore che ruoti a frequenza f costante[1].
Torniamo invece sul primo grafico della presente: sull'asse verticale
abbiamo rappresentato y(t) cioè il valore della tensione all'istante t. Si dice
ampiezza di un'onda il valore massimo che essa raggiunge. Nell'onda sinusoidale
il valore massimo positivo è uguale a quello negativo. Nel diagramma di cui
sopra il valore massimo è 311, quindi l'ampiezza YMAX = 311 (Volt).
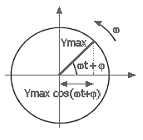In questo senso, y(t) è la proiezione sull’asse
verticale di un vettore di modulo YMAX
che ruota a velocità angolare costante in senso
antiorario, ovvero T è il tempo che il vettore impiega a compiere un angolo
giro completo, ruotando con frequenza f. Una cosinusoide è la sua proiezione
sull’asse orizzontale: in seguito ci riferiremo più spesso alla funzione
coseno.
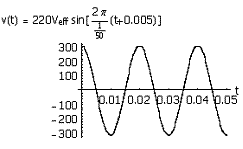
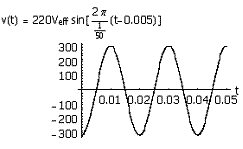
Scriviamo l’espressione della tensione sinusoidale in funzione del tempo come
(rispetto a prima, modifichiamo qui solo la notazione):
con 
sfasamento rispetto
allo zero (considerato finora nullo). In particolare, uno sfasamento trasla la
curva a sinistra (sfasamento positivo) od a destra (sfasamento negativo), come
mostrato rispettivamente di seguito.
Si definisce valore efficace di una grandezza elettrica sinusoidale il
valore equivalente che produce gli stessi effetti di riscaldamento della medesima
grandezza continua; è quindi legato alla potenza che tale grandezza è in grado
di trasferire ad un carico resistivo. Ovvero: una tensione continua (ad esempio
pari a 220 V) che alimenti un dato resistore produce effetti di riscaldamento equivalenti
ad una tensione alternata di medesimo valore efficace (220 V) che alimenti lo
stesso componente.
Il valore efficace di una tensione sinusoidale viene spesso indicato con Veff
(o semplicemente con
E’ così chiarito il motivo per il quale la tensione sinusoidale dei
nostri appartamenti viene comunemente quantificata a 220V mentre nel primo
grafico riportato la sua ampiezza è circa 311V.
Il valore quadratico medio, o efficace, è infatti definito, proprio per ragioni
legate alla potenza, come:
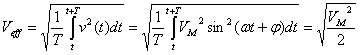
Analoghe considerazioni valgono per la corrente sinusoidale. Se indichiamo
con IM l'ampiezza (massima) della corrente, vale:
STUDIO
CIRCUITALE
Escluso il transitorio immediatamente successivo alla chiusura di un
circuito (lineare, tempoinvariante ed asintoticamente stabile), le correnti e
le tensioni circolanti nel circuito alimentato da generatori sinusoidali sono
anch’esse funzioni sinusoidali di ampiezza, frequenza (o pulsazione) e fase
costanti, ovvero sono funzioni descritte dalla soluzione particolare
dell’equazione differenziale associata, soluzione che non dipende dalle
condizioni iniziali. A regime, se i generatori sono sinusoidali della medesima
pulsazione , tutte le correnti e le tensioni circolanti nel circuito
avranno pulsazione , ma diversa ampiezza e fase tra loro[2].
Se ci disinteressiamo del transitorio e siamo interessati solamente al suo comportamento
a regime, un circuito dinamico alimentato da generatori sinusoidali può essere
risolto con tecniche molto meno difficoltose che la risoluzione di equazioni
differenziali, magari di ordine elevato.
L’importanza delle forzanti sinusoidali è inoltre dovuta all’asserzione
che ogni funzione periodica, sotto ipotesi assai generali, è esprimibile coma
sommatoria di funzioni sinusoidali (sviluppo in serie di Fourier). Si rimanda
alla Teoria dei Segnali per i dovuti approfondimenti.
VETTORI ROTANTI
e FASORI
Introdurremo ora un metodo di analisi che consente di risolvere i circuiti
in alternata sinusoidale, a regime, in modo formalmente analogo ai circuiti in
continua. Mediante opportuna scelta della fase, scriviamo i(t) e v(t) come
funzioni cosinusoidali, nient’altro che per semplicità di conti.
Ricordando che vale:[3]
definiamo fasore la grandezza:
così che:
dove Re{} indica la parte reale
del suo argomento.
Infatti:
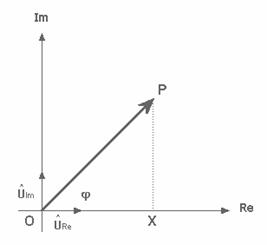
Nel piano complesso, 
è un vettore[4]
di lunghezza AM formante un certo angolo con l’asse reale.
è lo stesso vettore, in rotazione con velocità angolare in senso antiorario.
Graficamente: la
proiezione del vettore sull'asse reale (quindi la sua parte reale) coincide
istante per istante con la grandezza rappresentata dal fasore, grandezza (cosinusoidale)
avente valore massimo VM (IM)
e frequenza f.
Dato che, a regime, tutte le correnti e le tensioni circolanti nel
circuito avranno pulsazione , ogni grandezza sarà rappresentata da fasori rotanti tutti
con la stessa pulsazione.
Le associazioni grandezze/fasori divengono:
Infatti, ad
esempio:
a questo associamo:
dato
che:
Il metodo dei fasori consente di trasformare le equazioni differenziali
in equazioni algebriche, in campo complesso, nel seguente modo. Prendiamo come
esempio un circuito RLC parallelo alimentato da un generatore di corrente:
L’equazione differenziale governante il circuito è:
Se ora 
è il fasore di iL e
di AM cos(t + ), possiamo scrivere:
Notiamo che
appunto si tratta di equazione algebrica. In sintesi, abbiamo trattato i componenti
dinamici come resistori (impedenze), con queste regole:
L’impedenza di un
componente è definita come il rapporto tra la tensione vettore agente ai suoi
capi e la corrente vettore che attraversa tale componente e si misura in Ohm.
Per lo studio di
un circuito tratteremo direttamente i componenti dinamici come “resistori” di
impedenza[5] nota,
senza abbozzare nemmeno lo studio delle relative equazioni differenziali!
Quindi rimangono immutate le LKC e LKT.
Al termine dello
studio circuitale, con operazione inversa, si trasformeranno le grandezze
fasoriali in grandezze nel dominio del tempo:
NOTE
L’analogia tra fasori, trasformate di Laplace (ad argomento complesso) e
Fourier è fortissima. Si consiglia di approfondire l’argomento, trattato
generalmente nella Teoria dei Sistemi e nella Teoria dei Segnali.
Diamo uno sguardo ai componenti elettrici nel “dominio dei fasori” o, più
correttamente, nel dominio delle frequenze.
CIRCUITO
PURAMENTE RESISTIVO
Un circuito si
dice puramente resistivo quando
compaiono solo resistori.
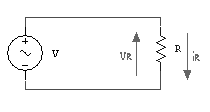
Nel circuito
puramente resistivo la corrente è in fase con la tensione (il resistore non
sfasa le sinusoidi di corrente e tensione).
Sia:
Risolviamo
innanzitutto per chiarezza il circuito nel dominio del tempo. Per il resistore
si ha:
Nel circuito di
cui sopra abbiamo inoltre:
Quindi:
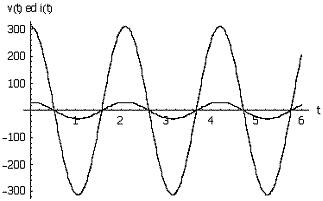
La forma d’onda
della corrente è identica a quella della forzante (tensione), fatta salva la
diversa ampiezza,Rvolte più piccola. Se, portando un esempio grafico, si
avessero:
le forme d’onda di
tensione e corrente sarebbero come da figura seguente.
Risoluzione fasoriale
La legge di Ohm applicata
ai fasori rappresentanti tensione e corrente implica che:
Con, per questo
particolare circuito:
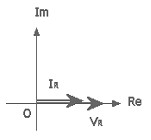
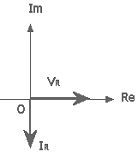
Il vettore
corrente è parallelo al vettore tensione, in quanto tensione e corrente sono in
fase, come visibile in entrambe le figure precedenti. E’ palese che per un
simile circuito, in cui mancano gli elementi dinamici, lo studio nel dominio
delle frequenze non è indispensabile (nota importantissima…).
CIRCUITO
PURAMENTE INDUTTIVO
Un circuito si
dice puramente induttivo quando in esso compaiono solo induttori. Lo schema
elettrico di un induttore alimentato da un generatore di tensione sinusoidale è
il seguente:
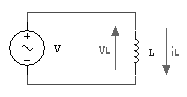
Sia:
Nel dominio del
tempo, per l’induttore si ha:
ovvero:
Nel circuito di
cui sopra abbiamo inoltre:
Quindi:
che coincide con:
L’integrale di una
grandezza sinusoidale (cosinusoidale) è una nuova grandezza sinusoidale
(cosinusoidale) sfasata di – 90°. Nella
fattispecie, tra tensione e corrente di un induttore esiste uno sfasamento di –
90°, con la corrente “in anticipo” rispetto alla tensione.
Risultati finali:
L’ampiezza della
sinusoide della corrente circolante nell’induttanza e quindi nell’intero circuito
è 
volte più piccola di
quella della tensione, dipendendo sempre dalla sua pulsazione.
Se, portando un
esempio grafico, si avessero:
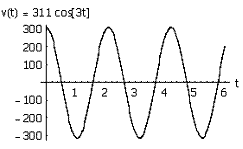
la forma d’onda
della corrente a regime[6] sarebbe,
matematicamente o nell’ipotesi che il generatore sia in grado di erogare tutta
la corrente calcolata:
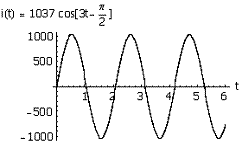
La scala dei due
grafici è ovviamente diversa. In ogni modo, “Ce la siamo cavata” con poco: non
è stato nemmeno necessario risolvere equazioni differenziali, tra l’altro. In
generale, tuttavia, con circuiti già appena più grandi, si dovrà per forza di
cose ricorrere alla tecnica fasoriale. Già con tre elementi dinamici abbiamo,
in caso di circuito non degenere, un’equazione differenziale di ordine tre. E
non è sempre cosa gradita doverla risolvere.
Risoluzione fasoriale
Per prima cosa
ricaviamo il fasore corrispondente alla forzante:
Riferiamoci ora
alla topologia circuitale. La legge di Ohm implica che, in regime sinusoidale,
per l’induttore valga:
con (nel
particolare caso del circuito in figura):
Quindi:
Il risultato
finale, nel dominio del tempo, sarà quindi, come ci aspettiamo:
Altre
informazioni:
Il modulo
della corrente circolante nell’induttanza è:
L’angolo tra asse
reale e vettore corrente, ovvero lo sfasamento tra tensione (il cui vettore qui
è parallelo all’asse reale) e corrente è:
Il fasore della
corrente quindi può essere anche scritto come:
Note in riferimento
a:
Possiamo pensare a
j come ad un operatore
matematico che, applicato alla corrente, la sfasa di 90° in anticipo rispetto
alla tensione; di conseguenza, dal suo punto di vista, la tensione è in ritardo
di 90° rispetto alla corrente.
Riferendoci al
piano complesso, se moltiplichiamo per j le componenti del vettore, possiamo
renderci conto dell’enunciato in maniera inequivocabile; nel dominio del tempo del
resto abbiamo già fatto le considerazioni sull’integrale di una grandezza
sinusoidale.
CIRCUITO
PURAMENTE CAPACITIVO
Un circuito si
dice puramente capacitivo quando in esso sono presenti solo condensatori. Lo
schema elettrico di un condensatore alimentato da un generatore di tensione
sinusoidale è il seguente:
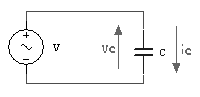
Sia:
Risolviamo
innanzitutto il circuito nel dominio del tempo. Per il condensatore si ha:
Nel circuito di
cui sopra abbiamo inoltre:
Quindi:
La derivata
temporale di una grandezza sinusoidale (cosinusoidale) è una nuova grandezza
sinusoidale (cosinusoidale) sfasata di + 90°. Nella fattispecie, tra tensione e
corrente di un condensatore esiste uno sfasamento di 90°, con la corrente “in
ritardo” rispetto alla tensione.
Risultati:
Tecnica fasoriale
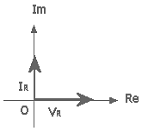
La legge di Ohm implica
che, in regime sinusoidale, per il condensatore valga:
Ovvero, per le proprietà del campo
complesso:
La tensione è in anticipo
di 90° rispetto alla corrente.
Quindi:
Il risultato finale, nel dominio del tempo, sarà quindi:
CIRCUITO RL
SERIE
Si dice circuito
RL un circuito in cui compaiono solo resistori ed induttori. Lo schema
elettrico di un RL serie alimentato da un generatore di tensione sinusoidale è
il seguente:
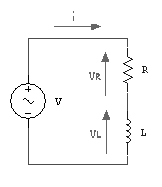
Nel circuito RL si
combinano i due effetti della resistenza del resistore R e della reattanza
induttiva[7] (modulo
dell'impedenza dell’induttanza) della bobina L, per cui si ha uno sfasamento
complessivo tra tensione e corrente che dipende da R e da ZL. L’impedenza di uno o più componenti elettrici,
informalmente, è l'ostacolo che questi oppongono al passaggio della
corrente alternata. L’impedenza totale vista
dal generatore (i due componenti sono in serie e quindi le loro impedenze si
sommano) è:
Il modulo 
dell’impedenza è, per
il Teorema di Pitagora applicato al piano complesso:
Per la legge di
Ohm:
in cui 
è la corrente che
attraversa la serie RL.
CIRCUITO RC
SERIE
Si dice circuito
RC un circuito in cui compaiono solo resistori e condensatori. Lo schema
elettrico di un RC serie alimentato da un generatore di tensione sinusoidale è
il seguente:
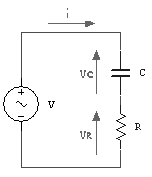
Nel circuito RC si
combinano i due effetti della resistenza del resistore R e della reattanza
capacitiva[8] del
condensatore C, per cui si ha uno sfasamento complessivo tra tensione e
corrente che dipende da R e da ZC. L’impedenza totale, vettore e modulo, vista dal
generatore vale (i due componenti sono in serie e quindi le loro impedenze si
sommano):
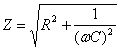
La legge di Ohm implica
che:
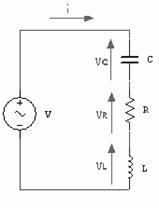
CIRCUITO RLC
SERIE
In un circuito RLC
compaiono resistori, induttanze e condensatori. Lo schema elettrico di un RLC
serie alimentato da un generatore di tensione sinusoidale è il seguente:
Nel circuito RLC
si combinano gli effetti della resistenza del resistore R, della reattanza
induttiva della bobina L e della reattanza capacitiva del condensatore C, per
cui si ha uno sfasamento complessivo tra tensione e corrente che dipende da R, ZL
e ZC. L’impedenza vista
dal generatore (i tre componenti sono in serie e quindi le loro impedenze si
sommano) vale:
Il modulo
dell’impedenza è:
La legge di Ohm implica
che:
RISONANZA – CENNI
Poiché la corrente
circolante in un circuito a forzante sinusoidale varia in dipendenza della
pulsazione , si ha risonanza quando la corrente raggiunge il suo valore
massimo. La pulsazione 
cui corrisponde IMAX
è detta pulsazione (o frequenza) di risonanza (o naturale), è caratteristica
del particolare circuito preso in esame ed è ricavabile dalla soluzione
dell’equazione differenziale che lo rappresenta o dalla tecnica fasoriale.
Quindi, quando la
pulsazione della forzante (generatore sinusoidale) eguaglia la pulsazione
naturale del circuito, questo entra in risonanza. In questa condizione,
tensione e corrente sono in fase tra loro.
Ad esempio,
considerando un circuito RLC serie alimentato da un generatore di tensione
sinusoidale, l’impedenza della serie RLC vale, come visto poco sopra:
Il modulo dipende
dalla pulsazione della tensione applicata. Per la legge di Ohm otteniamo:
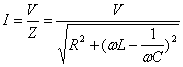
Grandezza che
dipende anch’essa dalla pulsazione . La corrente è quindi massima per:
POTENZA – CENNI nel dominio del tempo
Vogliamo calcolare
la potenza che un’impedenza Z scambia col generatore in un circuito a regime
sinusoidale, nel dominio del tempo.
Se ai capi
dell’impedenza Z si hanno (con direzioni di riferimento associate, secondo
consuetudine in Elettrotecnica):
La potenza
istantanea vale:
Il suo valor medio
in un periodo è:
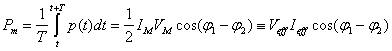
Dei tre componenti
visti, solo il resistore trasforma l’energia in calore per effetto Joule.
Autore: ing. Marco
Buratto.
Testo
originale tratto da www.scuolaelettrica.it,
a cura del prof. ing. Pietro De Paolis.
Per ogni segnalazione riguardante commenti,
comunicazioni di errori, omissioni, ingiurie varie….. e via dicendo, prego
scrivere a: marco.buratto@tiscali.it.
Contributi ben accetti. Cercansi traduttori.
E’ consentita
la riproduzione parziale o totale del presente testo, senza necessità
di permesso alcuno, purché vengano riportati autori e fonte.
angolo compreso tra il vettore e l’asse reale. Nel moto
circolare uniforme, la velocità angolare vale quanto sopra definito, essendo,
nell'arco di tempo T, l'angolo descritto dal raggio proprio un angolo giro.
:
. 
