Teoria della Risposta in Frequenza e Filtri Passivi
Si è visto come,
per un circuito a parametri concentrati, lineare[1],
tempoinvariante ed asintoticamente stabile[2], in
regime sinusoidale, la relazione tra il fasore della tensione – o più in generale
della forzante di ingresso – ed il fasore della corrente – o di altra grandezza
di uscita – fosse un certo valore complesso.
Considereremo di
qui in avanti sistemi SISO (Single Input Single Output), ovvero per ogni
circuito descritto avremo una sola forzante ed una sola uscita. Quanto detto in
precedenza ha validità generale: data una forzante sinusoidale, la grandezza
che definiremo come uscita sarà sinusoidale di pari pulsazione della grandezza
di ingresso. Il sistema non può generare in uscita frequenze non presenti in
ingresso, ma solamente amplificare od attenuare (quindi anche annullare) e
sfasare quelle presenti. Ciò valendo – lo ripeto – solamente per sistemi LTI
(lineari tempoinvarianti).
La relazione tra
uscita ed ingresso, in funzione di 
(dunque al variare di
tutte le possibili pulsazioni del segnale) viene detta risposta in frequenza
del sistema (circuito):
è anch’esso un numero
complesso, quindi rappresentabile nel piano complesso in notazione modulo e
fase:
La funzione di
risposta in frequenza descrive, in sostanza, il comportamento di un sistema
sollecitato da ogni possibile ingresso sinusoidale. Tuttavia, in virtù del
principio di sovrapposizione degli effetti per sistemi lineari, la nozione di
risposta in frequenza continua a valere anche per segnali non sinusoidali e non
periodici: è valida per ogni funzione (periodica) che possa esser sviluppata in
serie di Fourier, quindi approssimata quale sommatoria di termini sinusoidali,
o per ogni altra funzione che ammetta trasformata di Fourier – non sorprenda
sapere che sono qui comprese tutte le funzioni d’interesse pratico.
In sintesi, si è
introdotto il concetto di risposta in frequenza in modo semplice, basandoci
sulla teoria sui fasori precedentemente esposta, quindi si è precisato che è
possibile considerare classi di segnali ben più ampie delle funzioni
sinusoidali: la risposta in frequenza descrive ogni sistema LTI a parametri
concentrati asintoticamente stabile a regime[3]
nei confronti delle diverse componenti armoniche della variabile di ingresso.
Si consiglia vivamente
di approfondire la nozione di Trasformata di Fourier.
Per la seguente
trattazione, date le motivazioni appena accennate, di qui in avanti considereremo
e 
non più come fasori, ma come trasformata di Fourier di i(t) e
v(t) rispettivamente. Nel caso di semplici forzanti sinusoidali si ribadisce
che le due grandezze, trasformata e fasore, coincidono in quanto ad utilizzo
nello specifico.
Si dà il seguente
teorema fondamentale; le ipotesi sono le medesime di cui sopra.
Sia:
la grandezza in
ingresso al circuito.
L’uscita a regime
vale:
con:
, ampiezza massima
, sfasamento aggiuntivo.
Per ogni
condizione iniziale.
Nulla di nuovo: si
è solamente formalizzato quanto già visto negli esempi de “Il regime
sinusoidale”.
RAPPRESENTAZIONE GRAFICA
La forma più
utilizzata per la rappresentazione della risposta in frequenza è costituita dai
diagrammi di Bode, diagrammi che rappresentano, in funzione della pulsazione o
della frequenza, i suoi modulo e fase.
In tali diagrammi
la scala dei valori in ascissa è logaritmica di base 10.
Il diagramma del
modulo della funzione di risposta in frequenza riporta sulle ordinate, in scala
lineare, il valore di 
in decibel (dB). Per
convenzione:
Da tale
definizione si evince come valori maggiori, minori od uguali a zero della
grandezza in dB corrispondano rispettivamente a valori maggiori, minori od
uguali ad uno del modulo.
Nel diagramma
della fase, le ordinate riportano il valore dell’argomento della funzione di
risposta in frequenza, valore espresso in gradi o radianti ed in scala lineare.
I diagrammi di
modulo e fase della risposta in frequenza forniscono rispettivamente la
descrizione dell’amplificazione e dello sfasamento che il sistema produce nei
riguardi delle diverse armoniche del segnale di ingresso.
Nota
I diagrammi
presentati nel seguito sono stati disegnati tramite appositi software. A tal
proposito, va ricordato che esistono tecniche per il tracciamento manuale dei
diagrammi di Bode approssimati – di cui in questa sede non si dà cenno.
I FILTRI PASSIVI
Ogni circuito
reale si comporta come filtro nei confronti del segnale di ingresso in quanto
ne modifica lo spettro in accordo con la propria risposta in frequenza.
Filtro passivo passa basso
Un filtro passivo
passa basso è un circuito passivo che “lascia sostanzialmente passare” le
armoniche del segnale di ingresso di frequenza inferiore ad una frequenza data
(chiamata frequenza di taglio,
) ed attenua od elimina le rimanenti. Identicamente possiamo
riferirci alla pulsazione.
Poiché nella
pratica non è possibile che il modulo della funzione di risposta in frequenza sia
discontinuo, cioè non è possibile che questo si annulli per tutti gli 
avendo invece valore non
nullo per tutti gli 
, si definisce frequenza
di taglio di un filtro reale la frequenza alla quale, in termini
semplici, l’ampiezza massima[4]
della grandezza fisica in uscita è attenuata di 
volte.
Ovvero: la pulsazione di taglio
per un filtro passa basso è la pulsazione che rende vera la
seguente:
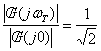
con:
guadagno del
filtro passa basso.
Di qui si ricava .
L’intervallo 
(oppure 
) è definito banda passante del sistema. Più è larga la banda
passante, più l’uscita assomiglia, eventualmente moltiplicata per un valore
costante, all’ingresso. Un sistema a banda larga è altresì un sistema “veloce”.
Affinché si abbia una fedele ricostruzione del segnale in ingresso è
importante, inoltre, non avere significative distorsioni di fase.
La pendenza di un
filtro si misura in dB/ottava ed indica di quanti dB diminuisce la grandezza di
uscita, nell’intorno della ed in funzione della
frequenza, in un’ottava, cioè ad un raddoppio della frequenza stessa.
|
Pendenza
del diagramma del modulo |
Ordine
del filtro passivo |
|
|
|
|
6
dB/ottava |
1
(un elemento dinamico) |
|
12
dB/ottava |
2
(due elementi dinamici, non degenere) |
|
18
dB/ottava |
3
(tre elementi dinamici, non degenere) |
|
24
dB/ottava |
4
(quattro elementi dinamici, non degenere) |
|
etc… |
|
Filtro passivo passa alto
Un filtro passivo
passa alto è un circuito passivo che “lascia passare” le armoniche del segnale
di ingresso di frequenza maggiore della ed attenua od elimina
le rimanenti. Identicamente possiamo riferirci alla pulsazione.
Come per i filtri
passa basso, si definisce frequenza di
taglio di un filtro reale la frequenza alla quale l’ampiezza massima della grandezza fisica in
uscita è attenuata di volte.
Per un filtro passa alto, la pulsazione di taglio è la pulsazione che rende vera la seguente:
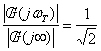
con:
guadagno del
filtro passa alto (se e solo se non nullo), inteso nel senso di limite. Di qui
si ricava .
oppure 
è la banda passante
del circuito.
Filtro passivo passa banda
Un filtro passivo
passa banda è un circuito passivo che “lascia passare” le armoniche del segnale
di ingresso di frequenza compresa tra le sue frequenze di taglio ed attenua od
elimina le rimanenti.
Filtro passivo di notch od a spillo
Un filtro passivo a
spillo è un circuito in grado di arrestare unicamente una (stretta) banda si
frequenze centrate attorno ad una frequenza data.
ALCUNI SEMPLICI ESEMPI DI FILTRI PASSIVI
Filtro passivo passa basso RC (primo ordine)
Un tipico circuito
passa basso di tipo RC è il seguente, in cui la variabile di uscita è
rappresentata dalla tensione sul condensatore:
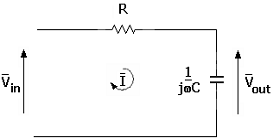
Di per sé, possiamo
pensare al condensatore come ad un componente in grado di lasciar passare
inalterate le armoniche di “alta” frequenza ed in grado di eliminare quelle di “bassa”
frequenza, dipendentemente appunto dalla sua capacità C (fissata R). Più la
capacità è piccola, più il condensatore riesce a “ricostruire” il suo ingresso
in tensione.
Nel circuito di
cui sopra il condensatore pone in corto verso massa queste alte frequenze, restituendo
in uscita solamente le frequenze basse.
Lo studio
circuitale impone:
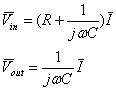
Di qui:
Modulo e fase di tale numero complesso sono
rispettivamente:
Il circuito non
presenta risonanza.
La pulsazione di
taglio, come detto, è la pulsazione alla quale il modulo della grandezza di
uscita viene attenuato di un fattore rispetto al suo valore
massimo. Poiché nel circuito in esame il guadagno del filtro è unitario, tale
ampiezza massima coincide con quella della grandezza in ingresso. In
riferimento al modulo della risposta in frequenza, quanto detto coincide quindi
matematicamente con:
Essendo R > 0 e C > 0 si ricava
facilmente:
Si notano due
cose:
1.
la pulsazione di taglio coincide con l’inverso della costante di tempo del
circuito stesso;
la fase della risposta
in frequenza vale:
.
Esempio
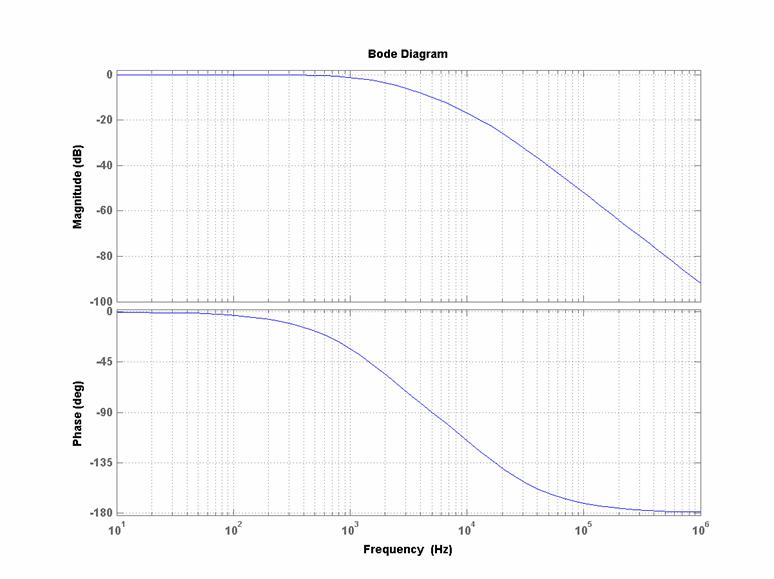
I diagrammi di Bode (reali) di modulo e fase per:
sono i seguenti:[5]
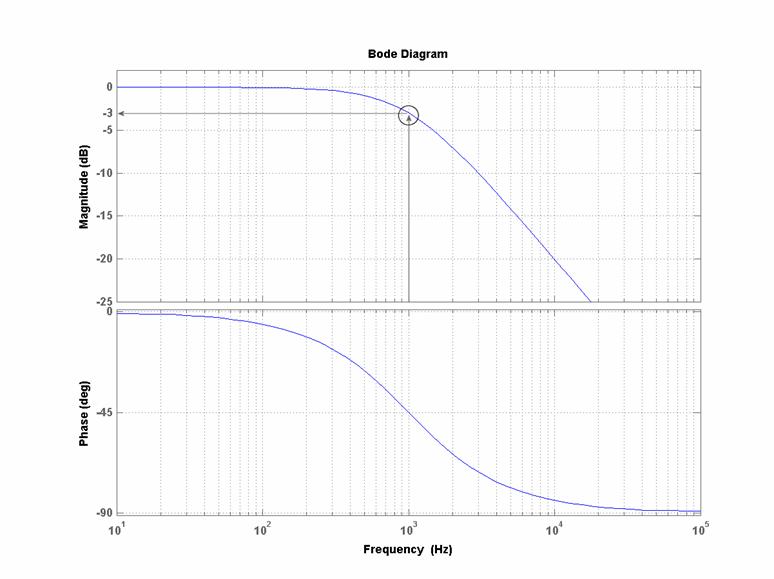
Notiamo che:
1. i grafici sono in scala logaritmica in
ascissa e lineare in ordinata, rispettivamente in dB quello del modulo ed in
gradi quello della fase. La scala logaritmica è qui espressa in Hz; spesso viene
espressa in rad/s;
2.
0 dB corrisponde
a guadagno unitario (rispetto alla grandezza di ingresso);
3.
il valore del
modulo alla frequenza di taglio vale -3 dB, ovvero 
volte il suo valore
massimo;
4.
il circuito in
esame rappresenta quindi un filtro passa basso del primo ordine; notiamo che
l’andamento del modulo cala di 6 dB per ottava nell’intorno della frequenza
(pulsazione) di taglio.
Filtro passivo passa alto RC (primo ordine)
Un tipico circuito
passa alto di tipo RC è il seguente, in cui la variabile di uscita è
rappresentata dalla tensione sul resistore. Il condensatore è posto in serie
tra ingresso ed uscita, ciò implicando che le “basse” frequenze vengono
attenuate od eliminate dallo stesso.
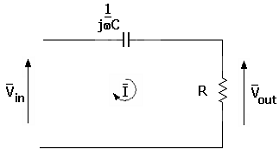
Lo studio
circuitale impone:
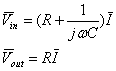
Di qui:
Modulo e fase di tale numero complesso sono
rispettivamente:
Il circuito non
presenta risonanza.
La pulsazione di
taglio vale:
Si nota che la
pulsazione di taglio coincide con l’inverso della costante di tempo del
circuito stesso.
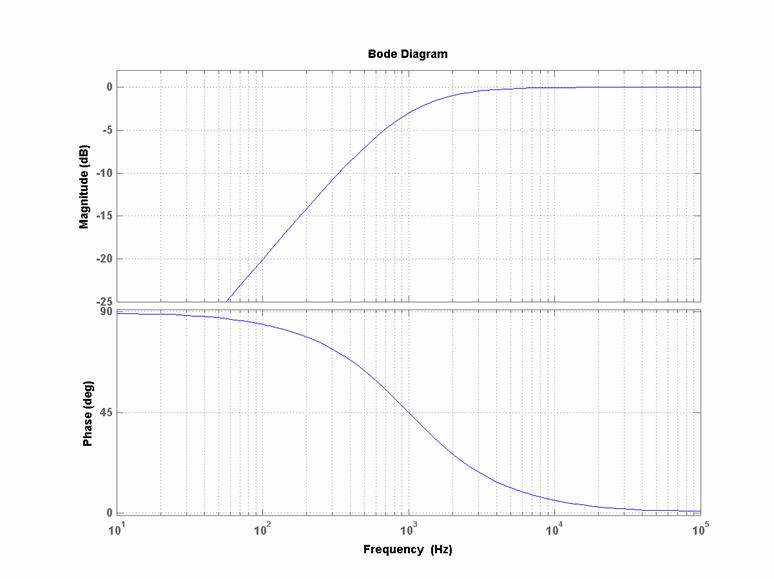
Esempio
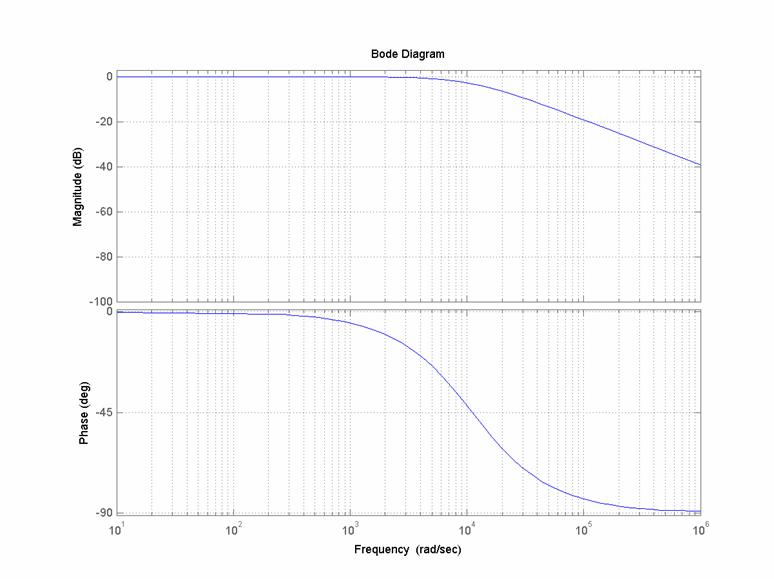
I diagrammi di Bode (reali) di modulo e fase
per:
sono i seguenti:
Filtro
passivo passa basso RL (primo ordine)
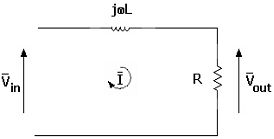
Di per sé, possiamo
pensare all’induttore come ad un componente in grado di lasciar passare
inalterate le armoniche di “bassa” frequenza ed in grado di eliminare quelle di
“alta” frequenza, dipendentemente appunto da L (fissata R). Più L è piccola,
meno l’induttore si oppone al passaggio del suo ingresso in corrente.
Abbiamo:
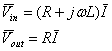
Di qui:
Modulo e fase di tale numero complesso sono
rispettivamente:
Il circuito non
presenta risonanza.
La pulsazione di
taglio vale:
Essendo R > 0 ed L > 0 si ricava
facilmente:
Si nota che la pulsazione di taglio coincide
con l’inverso della costante di tempo del circuito stesso.
Filtro passivo passa alto RL (primo ordine)
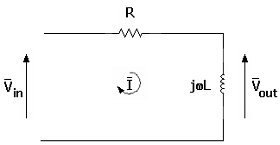
Al solito, usando il metodo agli anelli
otteniamo:
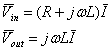
Di qui:
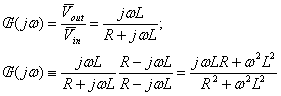
Modulo e fase di tale numero complesso sono rispettivamente:
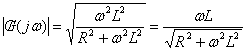
Il circuito non
presenta risonanza.
La pulsazione di
taglio vale:
Essendo R > 0 ed L > 0 si ricava
facilmente:
Si nota che la pulsazione di taglio coincide
con l’inverso della costante di tempo del circuito stesso.
I diagrammi di Bode (reali) di modulo e fase
per:
ad esempio per:
oppure
sono:
Filtro
passivo passa banda RLC serie (secondo ordine)
Si consideri come variabile di uscita la
tensione prelevata sul resistore di un circuito RLC serie alimentato in
tensione:
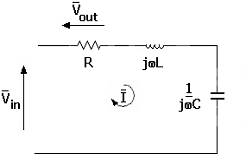
In regime sinusoidale si ha:
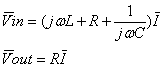
da cui si ricava che la funzione di risposta
in frequenza vale:
I cui modulo e fase sono rispettivamente:
Il circuito presenta risonanza (come visto ne
“Il regime sinusoidale”) per:
con 
pulsazione di
risonanza (si ricorda che a tale pulsazione il sistema si comporta come fosse
resistivo puro portando il modulo dell’impedenza vista dal generatore ad essere
minimo).
Calcoliamo la/le pulsazione/i di taglio,
cercando i valori per cui è verificata la seguente:
Da cui possiamo ottenere:[6]
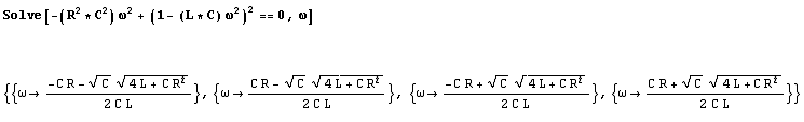
le cui soluzioni accettabili (a pulsazione
positiva) sono le ultime due, che possono essere riscritte come:
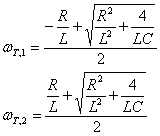
Si deduce che siamo
in presenza di un filtro passa banda in cui solo un insieme di frequenze in
ingresso (banda passante) viene attenuato per meno di un valore .
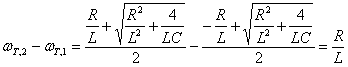
Ponendo:
pulsazione di risonanza e
banda passante, possiamo scrivere:
Esempi
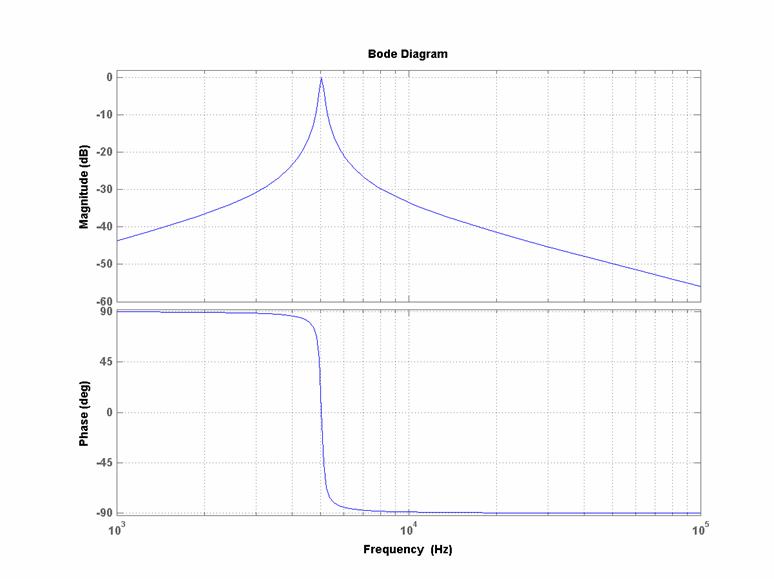
Diagrammi di Bode
(reali) di modulo e fase per:
quindi per una
banda passante che si estende da circa 4950 Hz fino a circa 5100 Hz:
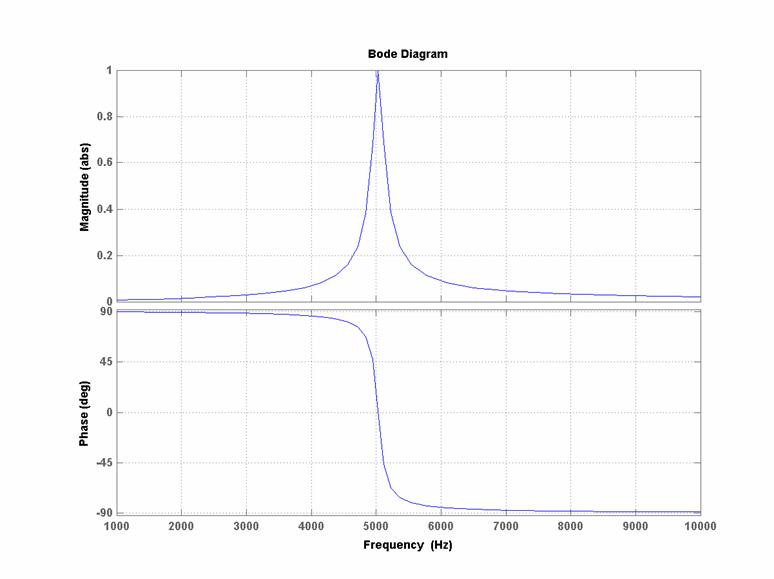
Per questi grafici
riporto anche l’equivalente in scala decimale in ascissa ed in scala decimale
ed in gradi in ordinata per modulo e fase rispettivamente:
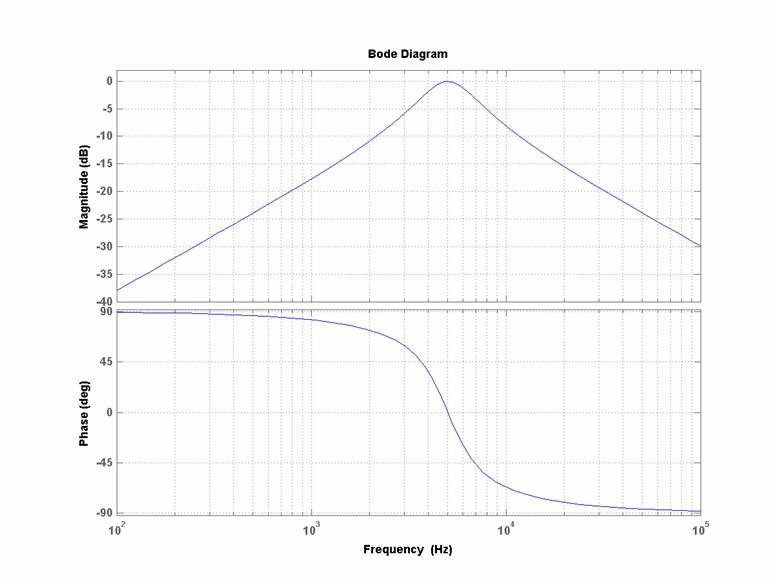
Diagrammi di Bode
(reali) di modulo e fase per:
quindi per una
banda passante che si estende da circa 3690 Hz fino a circa 6870 Hz:
In condizioni di risonanza:
1.
le tensioni sul
condensatore e sull’induttore sono di modulo uguale ma sfasate di 180°, ciò
implicando il loro annullamento matematico a livello macroscopico;
2.
lo sfasamento
dell’armonica a pulsazione è nullo.
Si definisce
fattore di merito Q il rapporto tra il modulo della tensione sull’induttore o
sul condensatore ed il modulo della tensione sul resistore alla pulsazione di
risonanza:
Q e B esprimono il
grado di selettività del filtro: la selettività è tanto maggiore quanto minore
è il valore della resistenza.
Diagrammi
di Bode di:
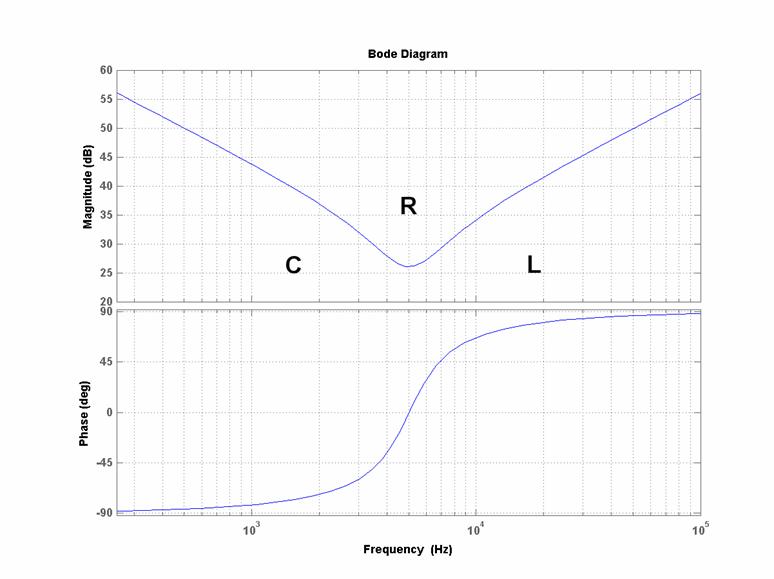
1.
A frequenze “basse”
il condensatore presenta un’elevata impedenza ed ostacola di conseguenza il
passaggio della corrente; contemporaneamente l’induttanza si comporta più o
meno come un corto circuito: il circuito nel suo insieme si dice
prevalentemente capacitivo.
2.
Man mano che
aumenta la frequenza si arriva alla frequenza di risonanza: il circuito si
comporta a tale frequenza come un semplice resistore (sfasamento nullo
dell’impedenza vista dal generatore).
3.
A frequenze
“elevate” l’induttore presenta un’elevata impedenza ed ostacola di conseguenza
il passaggio della corrente; contemporaneamente il condensatore si comporta sempre
più da corto circuito: il circuito si dice prevalentemente induttivo.
Filtro
passivo passa basso RLC serie (secondo ordine)
Si consideri come
variabile di uscita la tensione prelevata sul condensatore di un circuito RLC
serie alimentato in tensione. In regime sinusoidale si ha:
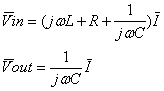
da cui si ricava che la funzione di risposta
in frequenza vale:
I cui modulo e fase sono rispettivamente:
Il circuito presenta risonanza in:
Calcoliamo la/le pulsazione/i di taglio:
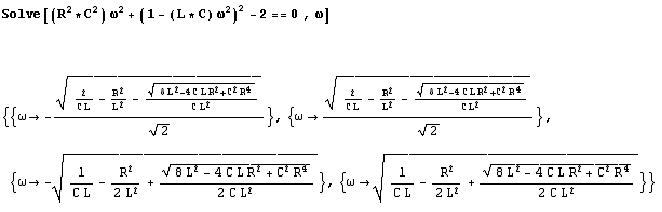
la cui soluzione accettabile è una sola,
l’ultima. Da ciò deduciamo di essere in presenza di un filtro passa basso.
Esempi
Diagrammi di Bode
(reali) di modulo e fase per:
:
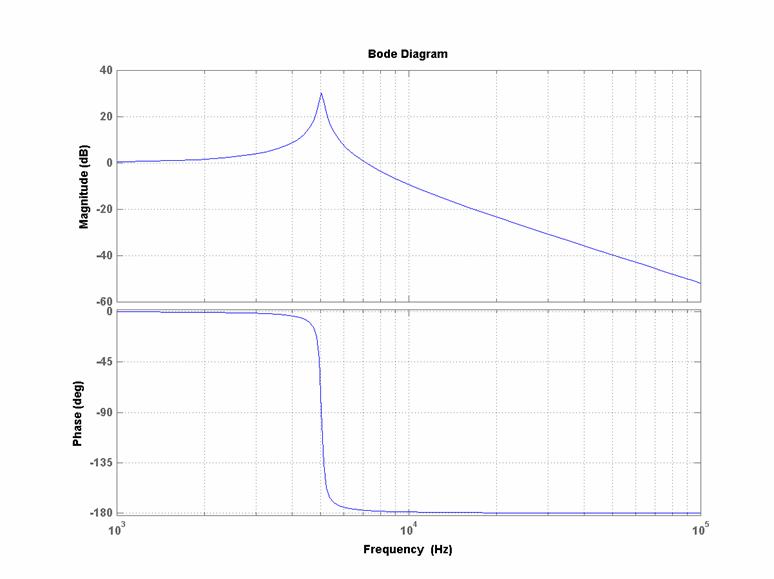
Più basso è il
coefficiente di smorzamento, più alto è il picco di risonanza.
Diagrammi di Bode
(reali) di modulo e fase per:
:
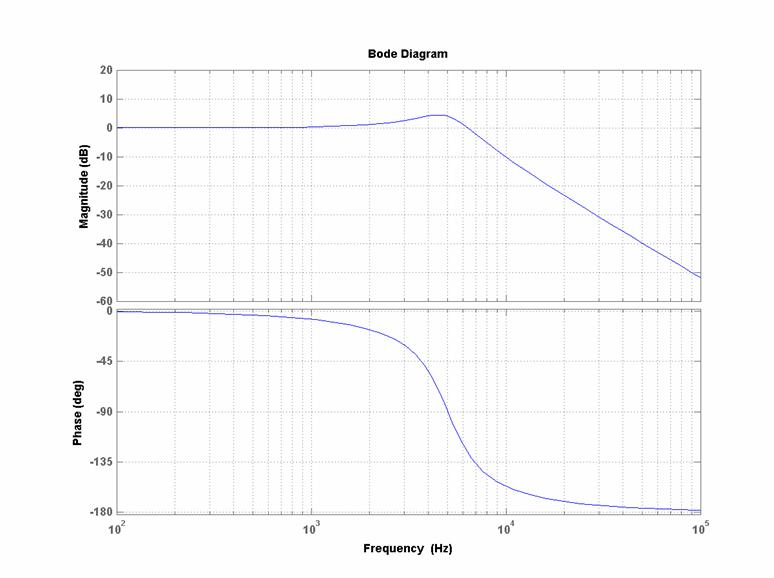
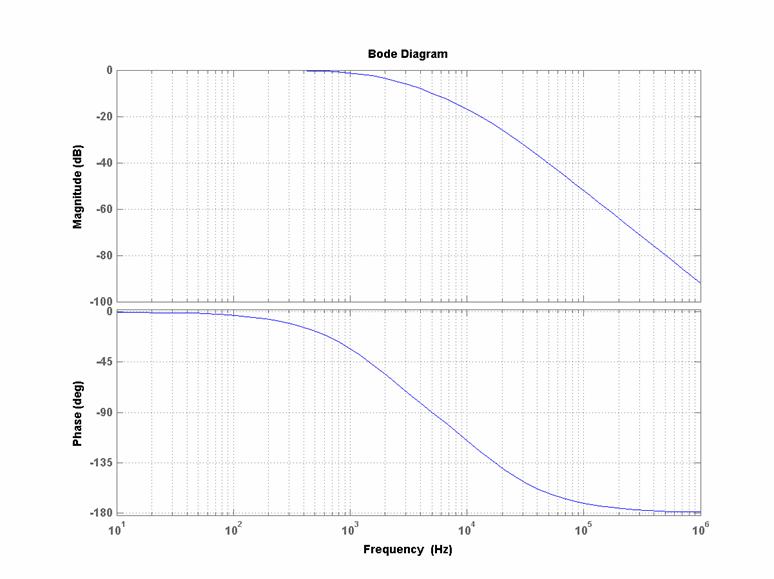
Diagrammi di Bode
(reali) di modulo e fase per:
:
Non tratteremo il
filtro passa alto RLC serie, in quanto molto simile al passa basso, ma ci
soffermeremo sul filtro a spillo.
Filtro a spillo (elimina banda) RLC serie (secondo
ordine)
Si consideri come
variabile di uscita la somma delle tensioni prelevate su condensatore ed
induttore di un circuito RLC serie alimentato in tensione. In regime
sinusoidale si ha:
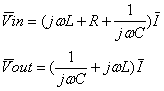
da cui si ricava che la funzione di risposta
in frequenza vale:
La/e pulsazione/i di taglio:
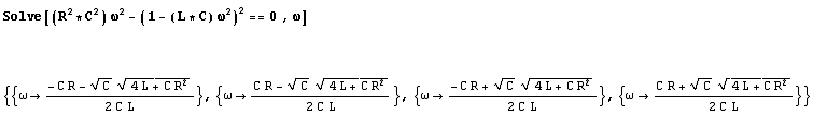
Le due soluzioni accettabili definiscono la
banda passante:
Esempi
Diagrammi di Bode
(reali) di modulo e fase per:
:
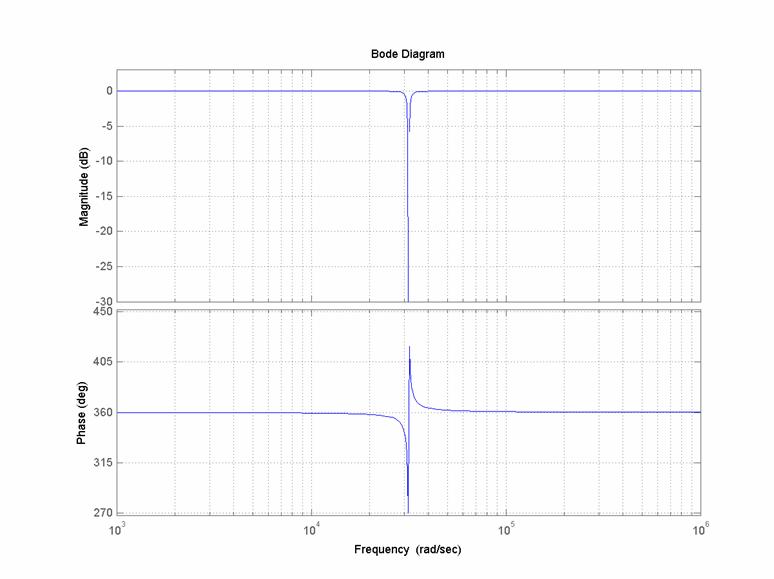
Diagrammi di Bode
(reali) di modulo e fase per:
:
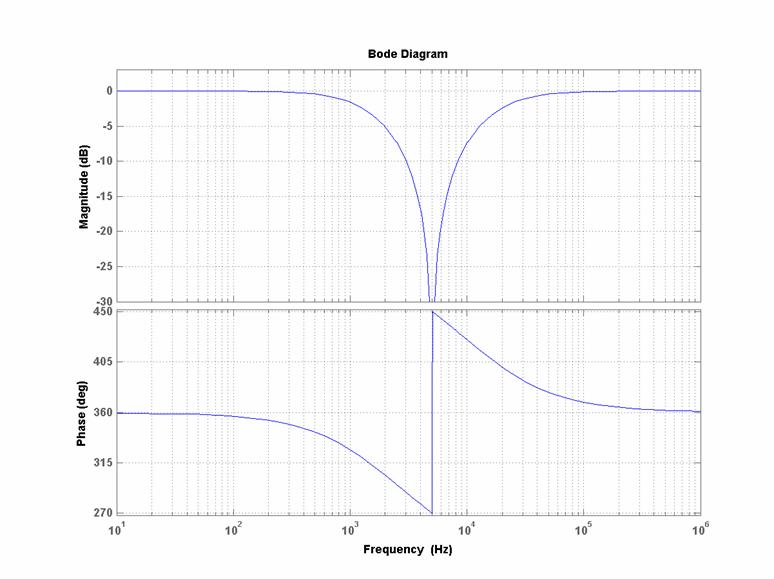
Filtro
passivo passa basso RLC della topologia in figura(secondo ordine)
Si consideri come
variabile di uscita la tensione prelevata sul resistore del circuito in figura:
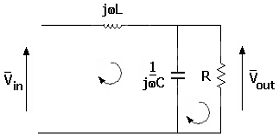
In regime
sinusoidale, usando il metodo agli anelli, otteniamo:
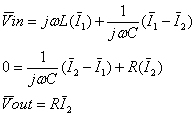
da cui si ricava che la funzione di risposta
in frequenza vale:
Calcoliamo la pulsazione di taglio:
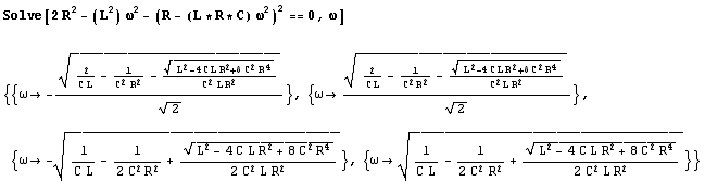
Soluzione accettabile: l’ultima.
Esempio
Diagrammi di Bode
(reali) di modulo e fase per:
che definiscono
per il filtro una frequenza di taglio di 1765 Hz (12 dB/ottava):
|
|
Un filtro passa
basso RC del primo ordine, invece, per la medesima frequenza di taglio presenta
il diagramma seguente. Si nota come il decadimento del modulo in funzione della
frequenza sia decisamente più lento (6 dB/ottava).
|
|
Per finire, esplicitiamo in
funzione di C, ovvero, date resistenza, induttanza e pulsazione di taglio,
diamo l’espressione che permetta di calcolare la capacità. Di estrema utilità
nel progetto dei filtri del crossover per casse acustiche.
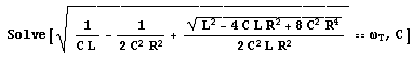
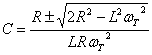
Se per semplicità di
conti poniamo:
allora il valore
della capacità del condensatore è vincolato ad essere:
Queste sono le
formule che si trovano con ricorrenza nella relativa letteratura.
Autore: ing. Marco
Buratto.
Contributi tratti da www.scuolaelettrica.it, a cura del
prof. ing. Pietro De Paolis.
Per ogni segnalazione riguardante commenti, comunicazioni
di errori, omissioni, ingiurie varie….. e via dicendo, prego scrivere a: marco.buratto@tiscali.it. Contributi
ben accetti. Cercansi traduttori.
E’ consentita
la riproduzione parziale o totale del presente testo, senza necessità
di permesso alcuno, purché venga riportato l’autore.