Errori dell'applicazione risolve la geometria

Osservazioni

sull'applicazione Android risolve la geometria.

L'applicazione è un calcolatore geometrico per scuola elementare e media; i problemi di aritmetica o di geometria per scuola superiore non vengono risolti.

Se non viene indicata nessuna misura del poligono, il problema non viene risolto.

traccia del 29/11/2016	osservazioni
Un rettangolo è equivalente a un quadrato il cui perimetro misura 96 cm; l'altezza del rettangolo è i 4/9 della base. Calcola la lunghezza del suo perimetro.	Problema non risolto a causa di un errore della applicazione. L'errore della applicazione è stato eliminato; ora il problema viene risolto in modo esatto.
Un settore ha l'area di 72π cm² che corrisponde a 2/9 dell'area del cerchio di appartenenza. Quanto misura il diametro del cerchio? Quanto è lungo l'arco corrispondente del settore?	Problema non risolto a causa di un errore della applicazione. L'errore della applicazione è stato eliminato; ora il problema viene risolto in modo esatto.
La base di un parallelogramma misura 73,2 dm ed è i 6/11 dell'altezza a essa relativa. Calcola l'area.	Problema non risolto a causa di un errore della applicazione; il problema veniva però risolto nella versione aggiornata a pagamento. L'errore della applicazione è stato eliminato; ora il problema viene risolto in modo esatto anche nella versione gratuita.

traccia del 28/11/2016	osservazioni
Il perimetro di un rettangolo è uguale al perimetro di un trapezio isoscele avente la somma delle basi di 38 dm e il lato obliquo di 10 dm. Sapendo che la base del rettangolo è 18/11 dell'altezza, calcola le loro rispettive misure.	Problema non risolto a causa di un errore della applicazione. L'errore della applicazione è stato eliminato; ora il problema viene risolto in modo esatto.
L'area della superficie totale di un parallelepipedo rettangolo è di 1432 cm² e le dimensioni delle sue basi sono lunghe 20 cm e 11 cm. Calcola l'altezza del solido.	Problema non risolto a causa di un errore della applicazione. L'errore della applicazione è stato eliminato; ora il problema viene risolto in modo esatto.

traccia del 27/11/2016	osservazioni
In un rombo un lato e l'altezza ad esso relativa misurano rispettivamente 24 centimetri e 20 centimetri. Calcola il perimetro e dall'area del rombo	Problema non risolto a causa di un errore della applicazione. L'errore della applicazione è stato eliminato; ora il problema viene risolto in modo esatto.
Un quadrato ha il perimetro di 112 cm ed è equivalente a un rettangolo avente l'altezza congruente a 4/7 del lato del quadrato. Calcola il perimetro del rettangolo.	Problema non risolto a causa di un errore della applicazione. L'errore della applicazione è stato eliminato; ora il problema viene risolto in modo esatto.

traccia del 26/11/2016	osservazioni
Il lato di un triangolo equilatero misura 27 cm. Calcola i raggi delle circonferenze inscritta e circoscritta al triangolo.	Problema non risolto completamente a causa di un errore della applicazione. L'errore della applicazione è stato eliminato; ora il problema viene risolto in modo esatto.
In un trapezio isoscele il perimetro è di 226 e il lato obliquo 65. Sapendo che la base minore è congruente a 1/2 della maggiore, calcola l'area del trapezio.	Problema non risolto a causa di un errore della applicazione. L'errore della applicazione è stato eliminato; ora il problema viene risolto in modo esatto.
I lati paralleli di un trapezio sono lunghi 15 cm e 23 cm e distano tra loro 7 cm Calcola l'area del trapezio	Problema non risolto a causa di un errore della applicazione. L'errore della applicazione è stato eliminato; ora il problema viene risolto in modo esatto.
Calcola l'area di un quadrato avendo il perimetro di 6m.	Problema non risolto a causa di un errore della applicazione. L'errore della applicazione è stato eliminato; ora il problema viene risolto in modo esatto.
Calcola l'area del cerchio circoscritto in un rombo avente l'area di 1536 cm² e una diagonale lunga 48 cm	Problema non risolto a causa di un errore della applicazione. L'errore della applicazione è stato eliminato; ora il problema viene risolto in modo esatto. Il cerchio è inscritto nel rombo, altrimenti sarebbe un quadrato.
In un rombo un lato e l'altezza ad esso relativa misurano rispettivamente 24 centimetri e 20 centimetri. Calcola il perimetro e dall'area del rombo	Problema non risolto a causa di un errore della applicazione. L'errore della applicazione è stato eliminato; ora il problema viene risolto in modo esatto.

traccia del 25/11/2016	osservazioni
Vi sono diverse richieste di problemi di aritmetica.	L'applicazione è un calcolatore geometrico per scuola elementare e media; i problemi di aritmetica o di geometria per scuola superiore non vengono risolti.
Un arco di circonferenza corrispondente ad un angolo di 40 gradi è lungo 28.26 cm. calcola la lunghezza del raggio della circonferenza a cui appartiene.	Problema non risolto a causa di un errore della applicazione. L'errore della applicazione è stato eliminato; ora il problema viene risolto in modo esatto. Svolgimento del problema Dati Figura geometrica: circonferenza angolo α = 40 ° arco l = 28,26 m Soluzione Si richiede la lunghezza del raggio r di una circonferenza sapendo che all'ampiezza dell'angolo α di 40 ° corrisponde l'arco l di 28,26 m Applico la formula: raggio r = ed ottengo: raggio r = = 40,479502417566 m Risposta Il raggio della circonferenza è 40,479502417566 m
La differenza tra due lati consecutivi di un paralellogramma misura 65 cm e uno dei due lati é 9/4 dell'altro. Calcola il perimetro.	Contiene un errore di battitura "paralellogramma" non previsto. Ora questo errore di battitura è tra quelli previsti dalla applicazione e il problema viene risolto correttamente.
calcola la differenza tra i raggi di due cerchi sapendo che il primo ha la circonferenza di 108 pi greco e il secondo ha l area di 961pi greco cm quadrati	Problema non risolto. Per ora non è prevista la soluzione tra più cerchi, ma tra un solo cerchio e un solo altro poligono.
un parallelogramma ha l'area di 405 cm e la base è lunga 7,5 cm e il lato consecutivo adesso è lungo il triplo della base trova la lunghezza dell'altezza relativa al lato	L'errore di battitura "adesso" viene trasformato in "ad esso". Il problema viene risolto correttamente.

traccia del 24/11/2016	osservazioni
Due triangoli sono equivalenti il primo ha l'altezza e la base rispettivamente di 21 cm e 14 cm; la base del secondo e congruente a 3/7 della base del primo. Calcola la misura dell'altezza del triangolo.	Problema non risolto. Per ora non è prevista la soluzione tra più triangoli, ma tra un solo triangolo e un solo altro poligono.
Disegna una circonferenza di centro O. Cosa noti?	Non disegna la circonferenza. Nel risolutore aggiornato la disegna. Svolgimento del problema
Disegna due circonferenze	Non disegna la circonferenza. Nel risolutore aggiornato ne disegna una sola.
La somma del diametro di una prima circonferenza con il raggio di una seconda circonferenza misura 63 cm e la loro differenza è 33 cm. Calcola la lunghezza dei due raggi	Problema non risolto. Per ora non è prevista la soluzione tra più cerchi o circonferenze, ma tra un solo cerchio e un solo altro poligono.
Calcola la lunghezza di una circonferenza sapendo che il suo raggio è congruente al lato di un triangolo equilatero avente il perimetro di 54 cm	Problema non risolto a causa di un errore della applicazione. L'errore della applicazione è stato eliminato. Svolgimento del problema Dati Poligono: triangolo equilatero ABC Perimetro p = 54 cm Svolgimento Si richiede il lato l di triangolo equilatero ABC il cui perimetro p = 54 cm Applico la formula: lato = ed ottengo: lato l = 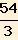= 18 cm Risposta Il lato del triangolo equilatero ABC è 18 cm Il raggio della circonferenza misura 18 cm. 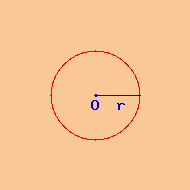Dati Figura geometrica: circonferenza Raggio r = 18 cm Soluzione Si richiede la circonferenza di un cerchio il cui raggio è: r = 18 cm Applico la formula: c = 2 x 3,14159 x raggio ed ottengo: c = 2 x 3,14159 x 18 cm = 113,09724 cm = 36π cm Risposta La circonferenza del cerchio è 113,09724 cm
Il diametro di una tovaglia circolare è di 2,4 m Calcola quanto si spende per orlare le tovaglie di una sala si ristorante con un pizzo che costa 17,20€ al metro, sapendo che il pizzo viene venduto a metri interi e che nella sala ci sono 22 tavoli	Problema non risolto. E' un problema di economia; non fa parte della geometria prevista in questo risolutore automatico.
Una circonferenza misura 72π e un altra ha un raggio uguale ai 5/9 del raggio della prima. Calcola la misura di una terza circonferenza che ha il raggio congruente alla differenza dei raggi delle circonferenze date.	Problema non risolto. Per ora non è prevista la soluzione tra più cerchi o circonferenze, ma tra un solo cerchio e un solo altro poligono.
La base di un rettangolo misura 62,2cm e l'altezza é congruente a quattro terzi di essa. Calcola il pperimetro del rettangolo	Contiene un errore di battitura "pperimetro" non previsto. Ora questo errore di battitura è tra quelli previsti dalla applicazione e il problema viene risolto correttamente. 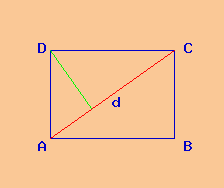Svolgimento del problema Calcolo altezza sapendo che: lunghezza = 62,2 cm rapporto = 4/3 Applico la formula: altezza = ed ottengo: altezza = = 46,65 cm Risposta altezza è 46,65 cm Dati Poligono: rettangolo ABCD base b = 62,2 cm altezza h = 46,65 cm Soluzione Si richiede il perimetro del rettangolo ABCD i cui lati sono: AB = 62,2 cm. BC = 46,65 cm Applico la formula: p = AB + BC + CD + DA ed ottengo: p = 62,2 cm + 46,65 cm + 62,2 cm + 46,65 cm = 217,7 cm Risposta Il perimetro del rettangolo ABCD è 217,7 cm.
Un quadrato è equivalente ai 14/3 di un rettangolo. Sapendo che il perimetro del rettangolo è 234 cm e che le sue dimensioni sono una i 7/6 dell'altra, calcola il perimetro del quadrato.	Problema non risolto a causa di un errore della applicazione. L'errore della applicazione è stato eliminato. Svolgimento del problema Calcolo semiperimetro del rettangolo sapendo che: perimetro = 234 cm divisore = 2 Applico la formula: semiperimetro del rettangolo = ed ottengo: semiperimetro del rettangolo = = 117 cm Risposta semiperimetro del rettangolo è 117 cm Dati La somma di base + altezza = 117 cm base = x altezza Soluzione Essendo base 7/6 volte altezza posso considerare che le parti della somma sono: 7 + 6 = 13 parti Ora divido la somma in 13 parti e ottengo = 9 cm Quindi base = 7 x 9 = 63 cm altezza = 6 x 9 = 54 cm Risposta base = 63 cm altezza = 54 cm Se conosco le equazioni posso usare un secondo metodo di risoluzione. 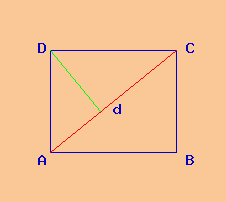Dati La somma di base + altezza = 117 cm base = 7/6 x altezza Soluzione Mi calcolo una equazione sapendo che base = 7/6 x altezza e che la somma di base + altezza = altezza + 7/6 x altezza = 117 cm da cui altezza = = = 54 cm base = 7/6 x altezza = 7/6 x 54 = 63 cm Risposta base = 63 cm altezza = 54 cm Dati Poligono: rettangolo ABCD base b = 63 cm altezza h = 54 cm Soluzione Si richiede l'area del rettangolo ABCD i cui lati sono: AB = 63 cm BC = 54 cm Applico la formula: A = AB x BC ed ottengo: A = 63 cm x 54 cm = 3402 cm² Risposta L'area del rettangolo ABCD è 3402 cm². L'area del quadrato è i 14/3 di 3402 cm² Calcolo area del quadrato sapendo che: area del rettangolo = 3402 cm² rapporto = 14/3 Applico la formula: area del quadrato = area del rettangolo x rapporto ed ottengo: area del quadrato = 3402 cm² x 14/3 = 15876 cm² Risposta area del quadrato è 15876 cm² L'area del quadrato è 15876 cm² Dati Poligono: quadrato ABCD area A = 15876 cm² Soluzione Si richiede il lato l del quadrato ABCD avente area A = 15876 cm². Applico la formula: l = V A ed ottengo: l = V 15876 = 126 cm Risposta Il lato del quadrato ABCD è 126 cm Dati Poligono: quadrato ABCD lato l = AB = 126 cm Soluzione Si richiede il perimetro del quadrato ABCD i cui lati sono: AB = BC = CD = DA = 126 cm Applico la formula: p = AB + BC + CD + DA ed ottengo: p = 126 cm + 126 cm + 126 cm + 126 cm = 504 cm Risposta Il perimetro del quadrato ABCD è 504 cm
Calcola l'ampiezza dell'angolo al centro di un settore circolare, sapendo che è 3/4 dell'intero cerchio.	Problema non risolto a causa di un errore della applicazione. L'errore della applicazione è stato eliminato. Svolgimento del problema Calcolo angolo al centro sapendo che: angolo giro = 360 ° rapporto = 3/4 Applico la formula: angolo al centro = angolo giro x rapporto ed ottengo: angolo al centro = 360 ° x 3/4 = 270 ° Risposta angolo al centro è 270 °
Calcola l'area di un segmento circolare corrispondente a un angolo al centro ampio 270° sapendo che il raggio del cerchio misura 50 cm.	Problema non risolto a causa di un errore della applicazione. L'errore della applicazione è stato eliminato. Svolgimento del problema Dati Figura geometrica: segmento circolare angolo α = 270 ° raggio r = 50 cm Soluzione Si richiede l'area del segmento circolare avente: angolo α = 270 ° raggio r = 50 cm Figura geometrica: circonferenza raggio r = 50 cm angolo al centro AÔB = α ( alfa ) = 270 ° Soluzione Si richiede la lunghezza della corda AB di una circonferenza avente: raggio r = 50 cm angolo al centro AÔB = α ( alfa ) = 270 ° Applico il teorema della corda: corda AB = 2 x r x sen = 2 x 50 x sen = 70,710678118655 cm Risposta La corda AB è 70,710678118655 cm Dati: Poligono: triangolo isoscele ABO base AB = 70,710678118655 cm lato obliquo BO = 50 cm Calcolo metà base sapendo che: base = 70,710678118655 cm divisore = 2 Applico la formula: metà base = ed ottengo: metà base = = 35,355339059327 cm Risposta metà base è 35,355339059327 cm Dati: Poligono: triangolo rettangolo HBO cateto c = HB = 35,355339059327 cm ipotenusa a = BO = 50 cm Soluzione Si richiede un cateto di un triangolo rettangolo HBO avente: cateto c = HB = metà base = 35,355339059327 cm ipotenusa a = BO = lato obliquo = 50 cm Applico la formula derivata dal teorema di Pitagora: cateto b = OH = altezza = V a² - c² ed ottengo: cateto b = V(50 cm)² - (35,355339059327 cm)² = 35,355339059328 cm Risposta L'altro cateto b = OH del triangolo rettangolo HBO, che coincide con altezza, è 35,355339059328 cm. Dati: Poligono: triangolo isoscele ABO base b = AB = 70,710678118655 cm altezza h = OH = 35,355339059328 cm Soluzione Calcolo l'area del triangolo isoscele ABO avente: base b = AB = 70,710678118655 cm altezza h = OH = 35,355339059328 cm applico la formula A = ed ottengo: A = = 1250 cm² Risposta L'area del triangolo isoscele ABO è 1250 cm² Dati Figura geometrica: settore circolare raggio r = 50 cm angolo del settore circolare α = 270 ° Soluzione Si richiede l'area del settore circolare di ampiezza α = 270 ° di un cerchio il cui raggio è: r = 50 cm Applico la formula: A_s = ed ottengo: A_s = = 5890,48125 cm² = 1875 π cm² Risposta L'area del settore circolare A_s è 5890,48125 cm² Eseguo la differenza tra l'area del settore circolare e l'area del triangolo ABO ed ottengo: area segmento circolare = 5890,48125 cm² - 1250 cm² = 4640,48125 cm² Risposta L'area del segmento circolare A_s è 4640,48125 cm²
Un quadrato e un rettangolo hanno lo stesso perimetro. Sapendo che il rettangolo ha l'area di 520 dm2 e la base lunga 26 dm calcola l'area del quadrato.	Problema non risolto a causa di un errore della applicazione. L'errore della applicazione è stato eliminato. Svolgimento del problema isoperimetrico vuol dire che il perimetro del rettangolo = perimetro del quadrato. Dati Poligono: rettangolo ABCD base b = 26 dm area A =520 dm² Soluzione Si richiede l'altezza del rettangolo ABCD avente: base b = 26 dm area A =520 dm² Applico la formula: h = ed ottengo: h = = 20 dm Risposta L'altezza del rettangolo ABCD è 20 dm. Dati Poligono: rettangolo ABCD base b = 26 dm altezza h = 20 dm Soluzione Si richiede il perimetro del rettangolo ABCD i cui lati sono: AB = 26 dm. BC = 20 dm Applico la formula: p = AB + BC + CD + DA ed ottengo: p = 26 dm + 20 dm + 26 dm + 20 dm = 92 dm Risposta Il perimetro del rettangolo ABCD è 92 dm. Il perimetro del quadrato è 92 dm Dati Poligono: quadrato ABCD Perimetro p = 92 dm Svolgimento Si richiede il lato l di quadrato ABCD il cui perimetro p = 92 dm Applico la formula: lato = 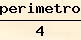ed ottengo: lato l = 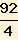= 23 dm Risposta Il lato del quadrato ABCD è 23 dm Dati Poligono: quadrato ABCD lato l = AB = 23 dm Soluzione Si richiede l'area di un quadrato ABCD i cui lati sono: AB = BC = CD = DA = 23 dm Applico la formula: A = lato x lato = AB x AB ed ottengo: A = 23 dm x 23 dm = 529 dm². Risposta L'area del quadrato ABCD è 529 dm².