 |
E = 12 V
R1 = 100 W R2 = 100 W R3 = 1.000 W R4 = 2.200 W
|
|
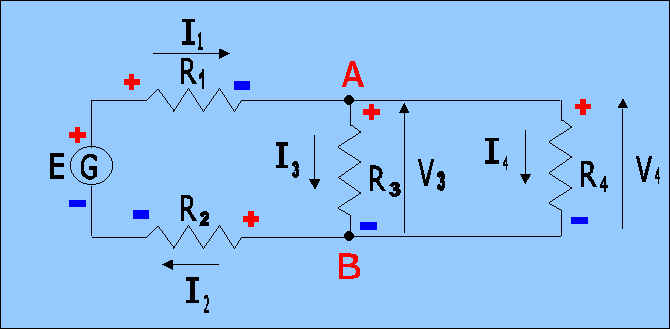
schema elettrico |
dati conosciuti |
Verifica sperimentale dei due principi di Kirchhoff
Scegliamo un circuito su cui misurare le correnti e le tensioni in modo da verificare i due principi di Kirchhoff, cioè quello delle correnti ai nodi e quello delle tensioni nelle maglie.
 |
E = 12 V
R1 = 100 W R2 = 100 W R3 = 1.000 W R4 = 2.200 W
|
|
schema elettrico |
dati conosciuti |
Come vediamo nel circuito nel nodo A vi sono tre correnti.
Il principio di Kirchhoff delle correnti dice che
in un qualunque nodo la somma delle correnti entranti è uguale alla somma delle correnti uscenti.Nel nodo A la formula è la seguente:
I1 = I3 + I4
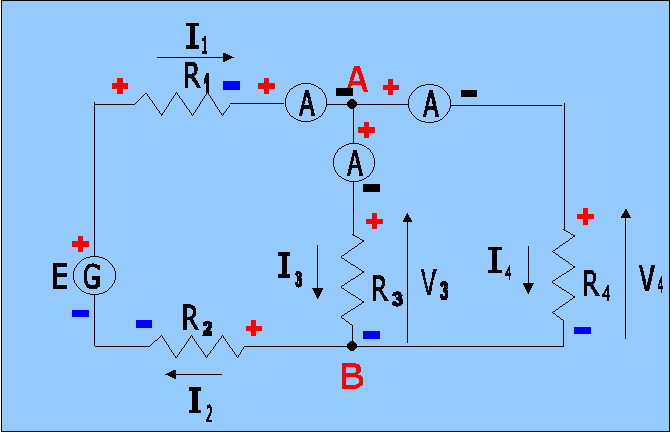
Ci servono allora tre amperometri da collegare in modo da misurare le tre correnti; poiché gli amperometri vanno collegati in serie al circuito in cui si misura la corrente, occorre interrompere i collegamenti del nodo A e inserire in ogni collegamento un amperometro. Lo schema elettrico di misura diventa il seguente:
 |
|
Schema elettrico di misura delle tre correnti nel nodo A |
Calcoli teorici
Prima di effettuare la misura in laboratorio ci facciamo dei calcoli teorici, in modo da poter usare le portate opportune dei voltmetri e degli amperometri. Ci calcoliamo ora tutte le tensioni e tutte le correnti del circuito.
Poiché i due resistori R3 ed R4 sono in parallelo ci calcoliamo la loro resistenza equivalente Rp:
Rp =
1
=
1 + 1 .
= 1
= 687,5
W
1 + 1 .
1000 2200 .
Sostituendo ai due resistori R3 ed R4 il loro parallelo Rp, il circuito diventa:
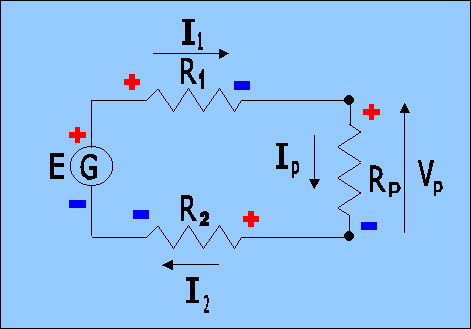 |
| circuito equivalente a quello iniziale |
Notiamo, ora, che i tre resistori sono collegati in serie e quindi ci calcoliamo la resistenza equivalente dei tre resistori collegati in serie:
RT = R1 + R2 + Rp = 100 + 100 + 687,5 = 887,5 W
Il circuito diventa:
|
|
|
Circuito equivalente a quello iniziale |
Con la legge di Ohm ci calcoliamo la corrente totale del circuito.
Vt = Rt x It
Ricaviamo la formula inversa e ci calcoliamo la corrente totale:
It
= Vt
= 12 = 0,0135211
A
Rt 887,5
Ritornando, ora, al circuito equivalente con i tre resistori in serie:
 |
| circuito equivalente a quello iniziale |
Essendo tutti i componenti collegati in serie avranno tutti la stessa corrente; quindi:
I1 = I2 = Ip = It = 0,0135211 A
Non resta ora che calcolare le tre tensioni dei tre resistori:
V1 = R1 x I1= 100 x 0,0135211 = 1,35211 V
Analogamente per R2 otteniamo:
V2 = R2 x I2= 100 x 0,0135211 = 1,35211 V
Analogamente per Rp otteniamo:
Vp = Rp x Ip= 687,5 x 0,0135211 = 9,29577 V
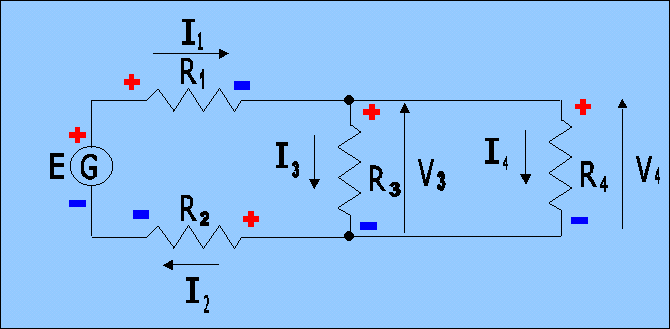 |
|
schema elettrico iniziale |
Ma poiché Rp rappresenta il parallelo tra R3 ed R4, vuol dire che sia R3 che R4 avranno la stessa tensione del parallelo, e cioè otteniamo:
V3 = V4 = Vp = 9,29577 V
Non resta ora che calcolare le due correnti dei due resistori in parallelo:
I3
= V3
= 9,295 = 0,009295
A
R3
1000
I4
= V4
= 9,295 = 0,004225
A
R4 2200
Misura in laboratorio
In laboratorio disponiamo dei resistori con tolleranza del 5% e di strumenti di misura di classe 0,5. Di conseguenza avremo che i valori di misura pratici saranno differenti da quelli teorici, a causa sia della tolleranza dei resistori che degli errori introdotti dagli strumenti di misura.
Controlliamo prima il nodo A. Ci prepariamo ora una tabella in cui scrivere i risultati della misura, e, dopo aver controllato tutti i collegamenti, possiamo accendere l'alimentatore di tensione continua da 12 V
| I1 [ mA] | I3 [ mA] | I4 [ mA] | I3+ I4 |
|
13,52 |
9,14 |
4,33 |
13,49 |
| lettura dell'amperometro | lettura dell'amperometro | lettura dell'amperometro | calcoli da fare |
Come avevamo previsto le misure delle correnti sono diverse da quelle teoriche, a causa della tolleranza del 5% sul valore teorico dei resistori e agli errori di misura dovuti agli strumenti.
Inoltre la somma delle due correnti uscenti è diversa da quella entrante a causa degli errori di misura introdotti dagli amperometri.
Tuttavia possiamo tranquillamente dire che il primo principio delle correnti è soddisfatto nel nodo A, a meno degli errori di misura, dovuti alla classe di precisione degli strumenti utilizzati.
Verifica di una maglia
Consideriamo la maglia esterna del circuito, costituita dal generatore E e dai tre resistori R1, R4, R2. Poiché vogliamo misurare le tensioni di tutti i componenti della maglia, mettiamo quattro voltmetri, ciascuno in parallelo ai quattro componenti della maglia.
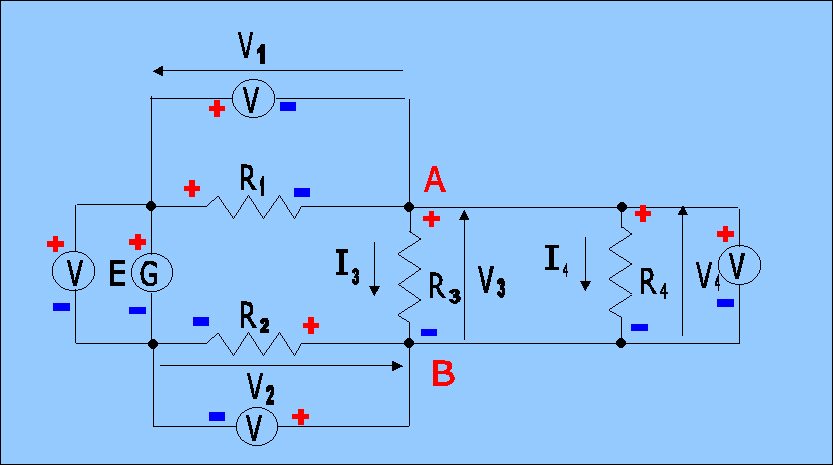 |
| circuito di misura |
Ci prepariamo ora una tabella in cui scrivere i risultati della misura, e, dopo aver controllato tutti i collegamenti, possiamo accendere l'alimentatore di tensione continua e regolarlo sui 12 V precisi.
| E [ V] | V1 [ V] | V4 [ V] | V2 [ V] |
|
12,00 |
1,32 |
9,36 |
1,30 |
| lettura del voltmetro | lettura del voltmetro | lettura del voltmetro | lettura del voltmetro |
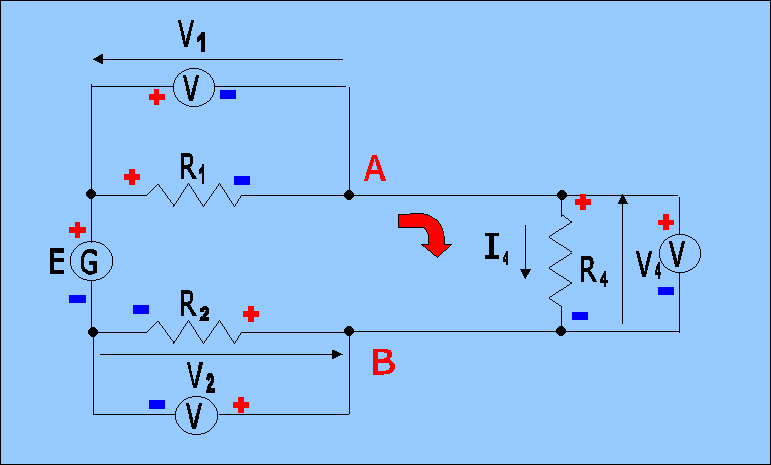
Vediamo, ora, se il secondo principio delle maglie è soddisfatto. Mettiamo i segni + e -vicino ad ogni resistore, e fissiamo un verso di percorrenza della maglia.
 |
|
Circuito per scrivere l'equazione della maglia esterna |
Applichiamo il secondo principio di Kirchhoff delle maglie. Facciamo prima la somma di tutti i generatori di tensione presenti, che poi è uno solo cioè E ; lo prendiamo col segno +, in quanto abbiamo incontrato prima il -. Anche le tre tensioni V1 e V4 e V2 le prendiamo col segno +, in quanto per i resistori il segno è concorde; quindi l'equazione della maglia sarà:
E = V1 + V4 +V2
Mettendo i valori dei calcoli teorici, otteniamo
12 = 1,35211 + 9,29577 + 1,35211 = 11,99999
e quindi possiamo dire che il secondo principio è soddisfatto per i valori teorici, a meno delle approssimazioni delle cifre decimali.
Mettendo, invece, i valori misurati, otteniamo:
12 = 1,32 + 9,36 + 1,30 = 11,98
e quindi possiamo dire che il secondo principio è soddisfatto anche per i valori misurati, a meno degli errori dovuti alla classe di precisione degli strumenti.
Osservazioni
In questa misura abbiamo semplificato i circuiti, trascurando sia le resistenze interne degli amperometri che le resistenze interne dei voltmetri. Infatti, se avessimo voluto fare le cose più precise, avremmo dovuto considerare nei calcoli teorici e in quelli pratici, non i valori dei resistori assegnati, ma quelli ottenuti:
1 - Per la misura delle correnti: la resistenza in serie di ciascun resistore sommata a quella interna del rispettivo amperometro;
2 - Per la misura delle tensioni: la resistenza di ciascun resistore in parallelo con la resistenza interna del rispettivo voltmetro.
In tal caso i calcoli sarebbero stati molto più complessi.
Elettrotecnica per istituti tecnici
Elettrotecnica ed elettronica per professionali
2003