La geometria analitica è un tool della matematica che ci permette di risolvere problemi difficilmente risolvibili per altre vie. In generale, si tratta di problemi geometrici e quindi la via alternativa alla geometria analitica viene chiamata geometria sintetica.
La geometria sintetica è la geometria di Euclide e delle dimostrazioni,conosciuta fin dall'antichità. Per contro, la geometria analitica ha origini nel seicento e deve la sua diffusione alle applicazioni, che nella nostra società industriale hanno avuto un successo travolgente, al punto che oggi la geometria sintetica è molto meno utilizzata di quanto lo fosse prima della scoperta della geometria analitica, e rischia perfino di essere dimenticata. Per contro, la geometria analitica si è trasformata in un calcolo algebrico sempre più astratto che rischia di ridurre l'intera matematica a un gioco di simboli privo di senso.
In questi problemi-risolti in seguito alla fine dell'unità- possiamo farci un'idea della potenza della geometria analitica
Esempio 1. Un proiettile viene sparato da un cannone di carro armato con una velocità iniziale di 100 m/secondo. Sapendo che l'alzo del cannone è di 30 o, determinare il punto di caduta e l'angolo di impatto del proiettile.
Esempio 2. Una piattaforma di telefonia mobile ha un canone di 10 euro e offre 1 minuto di conversazione a 0.5 centesimi. Una piattaforma di telefonia mobile ha un canone di 7 euro e offre 1 minuto di conversazione a 0.9 centesimi. Determinare qual'è l'offerta più conveniente.
Esempio 3. Una nave da crociera in navigazione a 40 miglia a Nord di Nassau ha un emergenza. Determinare l'unità di soccorso più vicina da cui far partire i soccorsi.
L'idea fondamentale della geometria analitica è la costruzione di una corrispondenza biunivoca tra i punti del piano e una coppia ordinata di numeri reali. In questo modo, ad una coppia di numeri reali sarà associato un punto del piano e a un punto del piano sarà associata una coppia di numeri reali. Vediamo come. Cominciamo con la costruzione di questa corrispondenza sulla retta.
Coordinate cartesiane sulla retta
Su una retta fissiamo
i) un verso di percorrenza
ii) un unità di misura
iii) un punto O, che chiamiamo origine

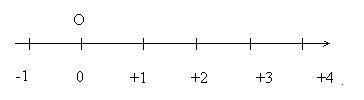
In questo modo si stabilisce una corrispondenza biunivoca tra i punti della retta e numeri reali. Per ogni punto sulla retta, il numero reale che corrisponde al punto si chiama coordinata o ascissa del punto.
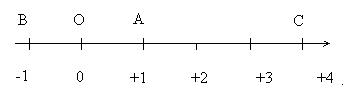
Esempio 1.1
Il punto A ha ascissa 1, il punto B ha ascissa -1, il punto C ha ascissa 4, il punto O ha ascissa 0.
La terna (r,O,u) si chiama sistema di riferimento cartesiano sulla retta ed è la struttura sulla retta che rende possibile la costruzione della corrispondenza cercata.L'estensione di questa struzione dalla retta al piano è immediata.
Siano due rette perpendicolari r ed s,, una verticale e una orizzontale-osserviamo che "orizzontale" e "verticale" non sono termini della matematica ma noi li capiamo senza problemi quando facciamo uso di carta quadrettata- e sia O il loro punto di intersezione. Fissiamo
i) un verso positivo sulla retta
orizzontale
ii) un verso positivo sulla retta verticale
iii) un'unità di misura u e un'unità di misura v sulle
due rette r ed s di cui ai punti i) e ii). Per semplicità,
u=v.
La struttura (O,r,s,u,v) si chiama sistema di riferimento cartesiano nel piano e in questo caso, per motivi cari ai fisici e alla loro didattica, è monometrico ortogonale. In ingegneria e in finanza capita spesso di avere sistemi di riferimento con diverse unità di misura. Nei corsi universitari di Geometria, le due rette r ed s si scelgono in maniera generica perchè l'esistenza di rette perpendicolari caratterizza astrazioni matematiche -dette "ambienti"- tanto ricchi quanto difficili a trovarsi, detti spazi di Hilbert. Gli spazi di Hilbert sono maturati nell'ambito di una comunità scientifica chiamata Circolo di Vienna e sono stati introdotti per lo studio della meccanica quantistica.
Fortunatamente, nel nostro mondo vale una proprietà degli spazi di Hilbert che conosciamo con il nome di Teorema di Piagora, e questo ci basta per adottare i sistemi di riferimento ortogonali.
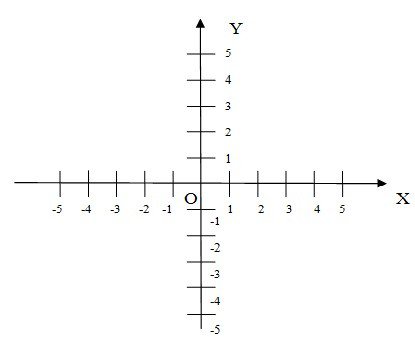
la retta orizzontale si chiama asse delle x, o asse x o asse delle ascisse. La retta verticale si chiama asse delle y o asse y o asse delle ordinate.
In un sistema di riferimento cartesiano -d'ora in avanti sarà sempre monometrico e ortogonale- è stabilita una corrispondenza biunivoca tra i punti del piano e le coppie ordinate di numeri reali.
Esempio 2.1
Sia il la coppia (2,3). Sull'asse x al numero 2 corrisponde il punto Ax. Analogamente, al numero 3 sull'asse y corrispinde il punto Ay . Per il punto Ax conduciamo la parallela all'asse y e per il punto Ay conduciamo la parallela all'asse x. Le due rette si intersecano nel punto A, che -per definizione- sarà la rappresentazione della coppia (2,3) nel sistema di riferimento cartesiano.
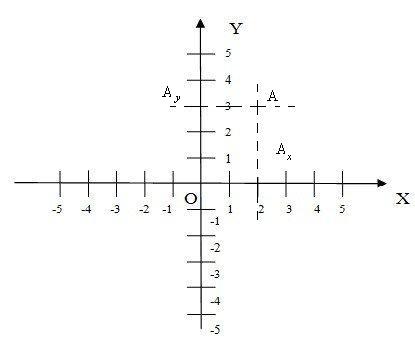
Analogamente, dato il punto A sul piano cartesiano, si tracciano le rette per A parallele all'asse y e all'asse x. Si ottengono i punti Ax e Ayle cui ascisse sono, rispettivamente, 2 e 3. La coppia (2,3) -nel riferimento cartesiano che abbiamo fissato-è la rappresentazione numerica del punto A. Il numero 2 si chiama ascissa di A, il numero 3 si chiama ordinata di A e la coppia ordinata (2,3) si chiama coordinate di A nel riferimento cartesiano.
L'idea delle coordinate cartesiane non è nuova: ci ricorda la battaglia navale. Anche qui abbiamo i quadranti, che sono per definizione i seguenti
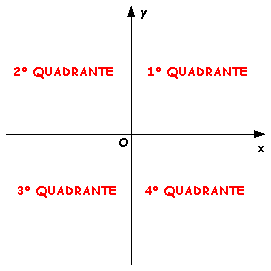
Il contenuto di questa pagina è interamente sotto la responsabilità dell'autore, Per segnalare imprecisioni ed errori, scirvere a ferrante.formato@istruzione.it .
Ultima modifica, 16 luglio 2015, ore 16.47
Domanda al professore a pagamento