4. La retta nel piano cartesiano
Per introdurre la retta nel piano cartesiano, è utile introdurre il concettto di luogo geometrico. I luoghi geometrici sono insiemi di punti nel piano. Per esempio, la circonferenza è l'insieme dei punti nel piano che hanno uguale distanza da un punto fissato. In molti casi, la geometria analitica consente di tradurre queste proprietà nel linguaggio delle equazioni. In questo caso, si ha una potente relazione che associa la goemetria all'algebra
un punto P appartiene a un luogo geometrico se le sue coordinate soddisfano l'equazione del luogo geometrico
Il concetto di varietà algebrica, estende quello di luogo geometrico.
Definizione 4.1 Una varietà algebrica nel piano cartesiano è l'insieme delle soluzioni di un sistema di equazioni algebriche in due incognite.
Esempio 4.1. Sia l'equazione
l'insieme delle soluzioni di questa equazione algebrica è una varietà algebrica nel piano cartesiano. In seguito scopriremo che si tratta di una nostra vecchia conoscenza, una circonferenza.
Esempio 4.2 Sia il seguente sistema di equazioni algebriche.
L'insieme delle sue soluzioni, {(0;1)} è una varietà algebrica nel piano. Si vede subito che essa rappresenta un punto, il punto di coordinate (0;1).
Esempio 4.3 Sia il sistema di equazioni
anche questa è una varietà algebrica, e il suo insieme di soluzioni è R2. Pertanto, il piano cartesiano è una varietà algebrica. In maniera analoga, si verifica che l'insieme vuoto è una varietà algebrica: infatti, è l'insieme di soluzioni di una equazione algebrica impossibile.
Tra le varietà algebriche, un posto di rilievo le occupano le varietà rappresentate da sistemi di equazioni di primo grado, dette varietà lineari. Tra queste, la più significativa sono i sistemi con una sola equazione, nella forma
Studiamo cosa significano queste varietà algebriche nel linguaggio della geometria. Osserviamo che la geometria analitica ci fornisce uno strumento potentissimo, che traduce il vocabolario della geometria in quello dell'algebra, risolve il problema algebrico e alla fine traduce la soluzione algebrica in una soluzione geometrica. Talmente potenete che oggi i matematici pensano in termini di "varietà", dimenticandosi spesso della interpretazione geometrica di questi oggetti e riducendo una dispiplina assolutamente affascinante in una serie di attività senza senso.
Se da un lato la geometria analitica ha aperto la matematica al mondo moderno-il mondo che va oltre i libri degli Antichi- ed ha aperto il mondo moderno alla matematica, dall'altro ha fornito alla matematica un'occasione per autodistruggersi.
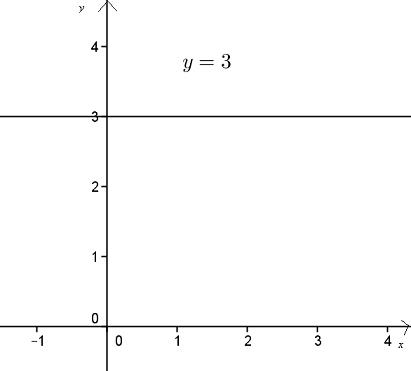
Sia l'equazione
![]()
si vede subito che le soluzioni di questa equazione sono le coppie di ordinata uguale a 3. Pertanto, questa equazione rappresenta una retta parallela all'asse x passante per il punto (0;3)
Teorema 4.1 Sia k un numero reale. L'equazione
![]()
rappresenta ua retta parallela all'asse x passante per il punto (0;k).
Analogamente, un' equazione nella forma x=k rappresenta una retta parallela all'asse y passante per il punto (k;0).
4.1 La retta passante per l'origine degli assi cartesiani
Sia l'equazione
![]()
e consideriamo i punti A(1;3), B(2;6) C(3;9). Questi coordinate sono soluzioni dell'equazione, pertanto i punti A,B e C appartengono alla figura geometrica rappresentata dall'equazione (1). Cerchiamo di rappresentare questa figura.
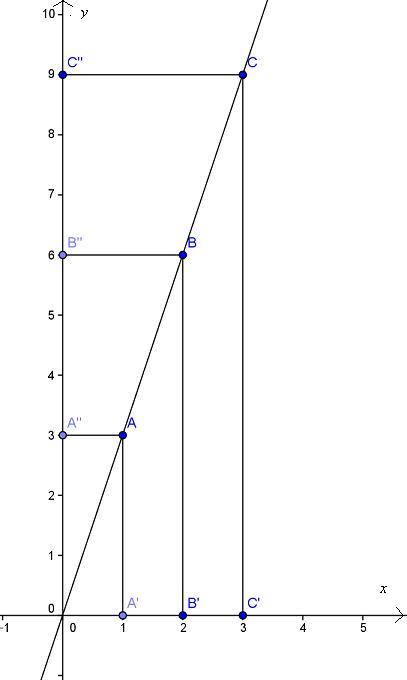
dalla similitudine dei triangoli OAA' e OBB'e OCC'si ricava che
AA'': AA' = BB'' : BB'=1:3
Di conseguenza i punti O, A, e B sono alllineati.
Ma anche i triangoli OAA' e OCC' sono simili. Di conseguenza
AA'':AA' = CC''=CC'=1:3
se ne deduce che O A e C sono allineati. Ma allora A,B e C sono allineati. In generale, i punti le cui coordinate sono soluzioni di (1) sono allineati. Siccome (0;0) è soluzione di (1), si deduce che l'insieme delle soluzioni dell'equazione (1) sono rappresentati da punti che stanno su una retta che passa per l'origine.
Viceversa, ogni punto P(x;y) di una retta che passa per l'origine, tale che
x:y=1:3
è soluzione dell'equazione (1).
Si conclude che l'equazione
![]()
è rappresentata nel piano cartesiano da una retta che passa per l'origine.
Teorema 4.2 Una equazione del tipo
è rappresentata nel piano cartesiano da una retta che passa per l'origine.
4.2 Il coefficiente angolare
Immagginiamo di avere un potenziometro e far variare il coefficiente m dell'aequazione
facciamo partire il cursore da 0 e spostiamolo verso destra, aumentando i valori di m. La retta sarà sempre crescente e l'inclinazione della retta aumenterà e la retta tende a coincidere con l'asse y.
Se invece , a partire da 0, spostiamo il cursore della retta verso sinistra, la retta sarà sempre decrescente e assume inclinazione sempre maggiore , fino a coincidere, al limite, con l'asse y
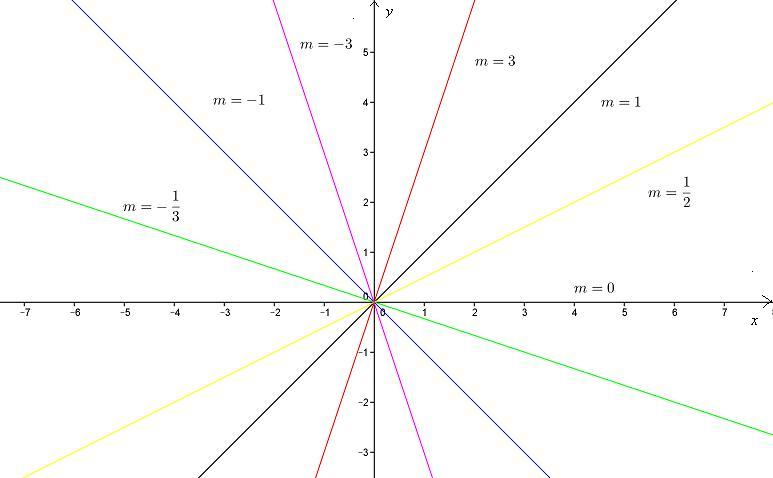
Il coefficiente m esprime in maniera qualitativa l'inclinazione della retta, e prende il nome di coefficiente angolare o pendenza
4.3 L'equazione canonica della retta
sia
![]() (2)
(2)
l'equazione di una retta che passa per l'origine. Trasliamo l'origine di una unità sulle ordinate. Nel linguaggio dellla fisica, introduciamo due osservatori, Lili e Freja. Lili si pone al centro del nostro sistema di coordinate, nel punto O(0,0). Per Lili, l'equazione della retta è quindi la (2). Vediamo come cambia l'equazione per Freja,che si pone nel punto di coordinate (0,1).La relazione tra le coordinate di Lili (O,x,y) e il sistema di coordinate di Freja (O',X,Y) è illustrata nel disegno seguente
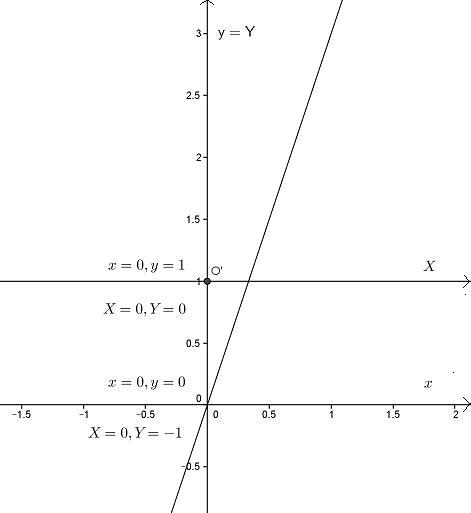
ed è espressa dalla seguente relazione
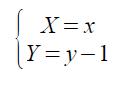
da cui
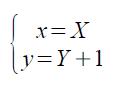
riscriviamo l'equazione della retta passante per l'origine -vista da Lili- nell'equazione di una retta che non passa per l'origine, vista da Freja
![]()
ovvero
![]()
nel sistema di riferimento di Freja, la retta non passa per l'origine e la sua equazione sarà
![]()
In generale, vale il seguente teorema, la cui dimostrazione estende il procedimento che abbiamo descritto
Teorema 4.3 Sia r una retta del piano cartesiano non parallela all'asse x. Allora esistono due numeri reali m ed n tali che l'equazione di r è
![]()
Infine, vale il seguente
Teorema 4.4 Sia r una retta qualsiasi nel piano cartesiano. Allora esistono tre numeri reali a,b,c tali che l'equazione della retta è
Dimostrazione: Descriviamo ciascun caso che si può verificare.
a) sia r una retta parallela all'asse x allora, posto a=0, l'equazione diventa
![]()
che risolta si scrive
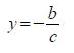
che è una retta del tipo y=k, ovvero una retta parallela all'asse y
b) sia r una retta parallela all'asse x. Posto b= 0 l'equazione diventa
![]()
che risolta si scrive
![]()
che è una retta del tipo x=k, ovvero una retta parallela all'asse x
c) sia r una retta passante per l'origine. Posto c=0 l'equazione diventa
![]()
da cui
![]()
e infine
![]()
che è un'equazione del tipo y=mx e rappresenta una retta passante per l'origine degli assi cartesiani.
d) sia r una retta generica, non parallela all'asse y, allora
![]()
e quindi
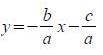 .
(3)
.
(3)
L'equazione (1)
si chiama forma canonica o forma implicita dell'equazione della retta.
Per contro, l'equazione
![]()
si chiama forma esplicita dell'equazione della retta. Siccome la forma canonica si riscrive come la (3), la relazione che lega le due equazioni è data da
il coefficiente m, lo sappiamo già- si chiama coefficiente angolare, e il coefficiente n-lo vedremo tra poco perchè- si chiama intercetta.
Il contenuto di questa pagina è interamente sotto la responsabilità dell'autore, Per imprcisioni ed errori, scirvere a ferrante.formato@istruzione.it .
Ultima modifica, 17 luglio 2015, ore 11.32