9.Applicazioni alla Matematica Finanziaria
Il calcolo del punto di pareggio nel bilancio aziendale
In questo capitolo si applica essenzialmente la Geometria analitica alla matematica finanziaria. Per approfondimenti di natura tecnica, si rimanda alla trattazione sulla Organizzazione Aziendale
Il costo è il prezzo che si paga per acquistare un bene o fruire di un servizio. Il ricavo è la somma che si riceve dal cliente a seguito della vendita di un prodotto o della prestazione di un servizio. Un azienda sarà in attivo -con un utile- se i suoi ricavi sono maggiori dei costi. In caso contrario, l'azienda sarà in perdita.
Esempio 9.1 la Mofongo.Biz, un'azienda di street food, in una sagra ricava 700 euro con un costo di 100 euro. E' andata in attivo e il suo utile è di 600 euro In un'altra sagra, Mofongo spende 150 euro e ne ricava 100. La perdita è di 50 euro.
Il reddito è la somma ottenuta dal conteggio dei costi, dal conteggio dei ricavi e dal calcolo della differenza tra ricavi e costi. Esso quindi può essere sia positivo che negativo.
Un ciclo economico aziendale è un processo che inizia con un investimento iniziale in cui vanno sostenuti dei costi, prosegue con una fase produttiva e termina con un ricavo, poi riprende.
Per determinare il prezzo di vendita di un prodotto occorre dapprima conoscere tutti i costi; poi alla somma dei costi si aggiunge l'utile che l'azienda vuole ottenere, e si ottiene così il prezzo:
Nel sistema analitico di rilevazione dei prezzi si fa uso di una scheda di costo per ogni prodotto; in ogni scheda si conteggiano sia i costi delle materie prime necessarie per la produzione del singolo prodotto, sia i costi della manodopera necessaria nelle officine di produzione, sia l'esatto quota dei costi dei macchinari da imputare al singolo prodotto, e sia l'esatta quota della incidenza delle spese generali sul singolo prodotto.
Berliner
Bratkartoffeln |
||||
| Descrizione materie prime | consumo unitario | costo unitario | costo totale in € | |
| Cipolle | 1 | 0,99 | 0,99 | |
| Speck a pezzetti | 0,1 | 2,25 | 1 | |
| Sale | 0.15 | 0,66 | 0,099 | |
| Pepe | 0,5 | 1,19 | 0,6 | |
| Paprika in polvere | 0,5 | 1,92 | 0,96 | |
| Patate | 0,5 | 0,98 | 0,49 | |
| Totale costo materie prime | 5,15 | |||
| Descrizione manodopera diretta | Tempo Unitario | Costo Orario | Costo Totale in € | |
| Cucina | 0.16 | 5,00 | 0,83 | |
| Totale costo manodopera | 0,83 € | |||
| Quote spese generali fisse | ||||
| Miscela per l'Ape | 1,45 | 4 | 5,8 | |
| Gas per cucinare | 4,75 | 2 | 9,5 | |
| Corrente elettrica | 4 | 27,59 | 27,59 | |
| Riparazioni di Zio Romolo | 1 | 20 | 20 | |
| Noleggio dell'Ape del macellaio di Chianchetelle | 1 | 25 | 25 | |
| Totale spese generali fisse | 87,89 | |||
Costi fissi e costi variabili. Rappresentazione cartesiana
Abbiamo visto che i costi fissi dell'azienda Mofongo.Biz sono di 87,89 € e la preparazione di un piatto di Berliner Bratkartoffeln costa
1,33 € +11,01 € = 12,34 €
Rappresentiamo i costi fissi con l'equazione
C = 87,89
Rappresentiamo i costi variabili con l'equazione
C = 12,34 p
Rappresentiamo le due equazioni in un piano cartesiano in cui l'asse x rappresenta il numero dei piatti preparati , e l'asse y rappresenta i costi

La somma dei costi fissi e dei costi variabili sono i costi totali, e si rappresentano con l'equazione
C = 87,89 + 12,34 p
graficamente

Costi fissi unitari
E' ovvio che la tabella scritta sopra non può essere usata per stabilire il prezzo delle nostre patate berlinesi. Infatti, un piatto di patate che costa 90 euro non lo compra nessuno!. Di conseguenza, occorre definire i costi fissi per piatti di patate, i costi fissi unitari.
Premettiamo che nel lungo periodo non esistono costi fissi.
Il costo fisso unitario è una funzione. La variabile indipendente è la quantità di panini cucinati.
Definizione 1 Il costo totale unitario (CTU) è il costo totale diviso la quantità prodotta.
Definizione 2. Il costo fisso unitario (CFU) si calcola come il costo fisso diviso la quantità prodotta.
Definizione 3 Il costo variabile unitario (CVU) si calcola come il costo variabile diviso la quantità prodotta.
Definizione 4 Il costo marginale é il costo aggiuntivo necessario per la produzione di una ulteriore unità di prodotto.
Esempio
| Quantità prodotte | Costi Fissi | Costi Variabili | Costi Totali | 0 | 300 | 0 | 300 |
| 1 | 300 | 150 | 450 |
| 2 | 300 | 270 | 570 |
| 3 | 300 | 370 | 670 |
| 4 | 300 | 480 | 780 |
| 5 | 300 | 600 | 900 |
| 6 | 300 | 740 | 1040 |
| 7 | 300 | 900 | 1200 |
| 8 | 300 | 1090 | 1390 |
| 9 | 300 | 1340 | 1640 |
| 10 | 300 | 1660 | 1960 |
| 11 | 300 | 2160 | 2460 |
Il grafico dei costi è in figura
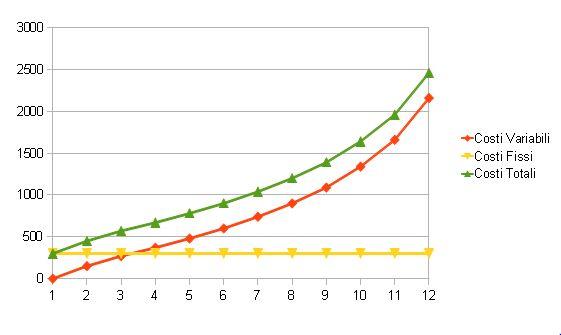
La legge dei rendimenti decrescenti impone che la curva dei costi variabili sia "più che lineare" oltre una certa soglia. Infatti, a partire da una certa quantità di merci prodotte, il numero di risorse necessarie a produrle aumenta e quindi aumentano i costi di produzione. Notiamo che i costi totali marginali sono espressi da una funzione di Q
Esempio Nella tabella 2, il costo marginale per la produzione di 4 unità è 780-670 = 110 euro
In economia aziendale la funzione dei costi marginali è estremamente importante. Se la quantità q è una grandezza continua, il costo marginale diventa una derivata prima: la derivata prima della funzione dei costi totali.
Vediamo adesso cosa succede ai costi unitari di produzione.
| Quantità | Costi Fissi Unitari | Costi Variabili Unitari | Costi Totali Unitari | Costi Marginali |
| 0 | - | - | - | - |
| 1 | 300 | 150 | 450 | 150 |
| 2 | 150 | 135 | 285 | 120 |
| 3 | 100 | 123 | 223 | 100 |
| 4 | 75 | 120 | 195 | 110 |
| 5 | 60 | 120 | 180 | 120 |
| 6 | 50 | 123 | 173 | 140 |
| 7 | 43 | 128 | 171 | 160 |
| 8 | 38 | 136 | 174 | 190 |
| 9 | 33 | 149 | 182 | 250 |
| 10 | 30 | 166 | 196 | 320 |
| 11 | 27 | 196 | 223 | 500 |
In forma grafica
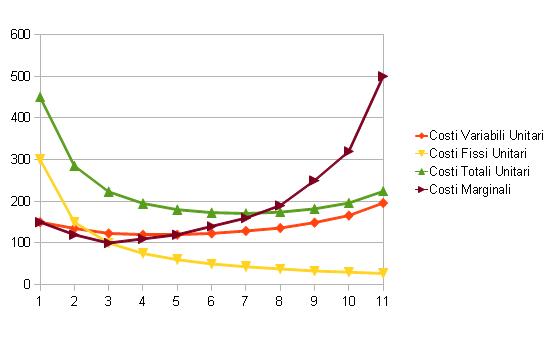
L’andamento dei costi totali
unitari assume la forma ad U a causa delle ipotesi che abbiamo fatto sulla
funzione di produzione: per le primissime unità prodotte il costo medio
scende, e poi sale. La forma delle curve del costo variabile unitario ed del
costo marginale dipendono dalla forma del costo totale unitario, e hanno queste
proprietà derivate da quelle della curva dei costi totali.La curva
del costo variabile unitario `e sempre inferiore alla curva del
costo totale unitario. Infatti, la differenza tra le due curve `e costituita
dalla curva del costo fisso unitario. Per definizione, i costi
fissi totali non variano al variare della quantit`a prodotta, per cui al crescere
della quantit`a i costi fissi unitari diminuiscono: la stessa cifra si “spalma”
su quantit`a crescenti di beni.
Proposizione 4.1.1 La curva dei costi marginali interseca la curva dei costi totali unitari e dei costi variabili unitari nei rispettivi punti di minimo
Corollario I costi unitari di produzione decrescono solo se i costi marginali sono più bassi
Il contenuto di questa pagina è interamente sotto la responsabilità dell'autore, Per imprecisioni ed errori, scrivere a ferrante.formato@istruzione.it .
Ultima modifica, 3 agosto 2015 ore 18:36