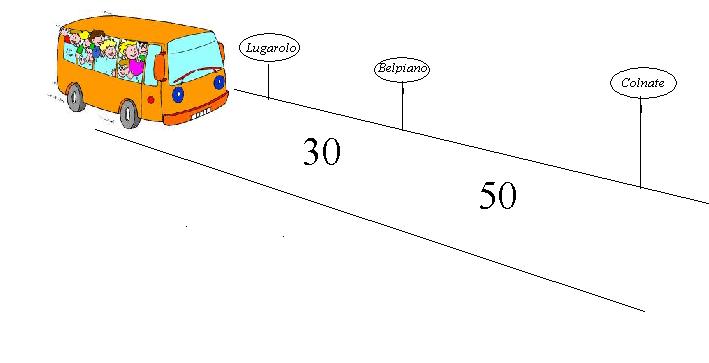
Una corriera deve andare da Lugarolo a Belpiano e da Belpiano a Colnate. Le distanza di Belpiano e Colnate da Lugarolo sono rispettivamente di 30 km e 50 km. Quanto distano Colnate e Belpiano? La situazione è disegnata in figura.

Dalla figura si intuisce che la distanza tra Belpiano e Colnate è 50 km -30 km= 20 km. E' questa l'idea di distanza tra due punti nel piano cartesiano. E' chiaro che potevamo fare anche 30-50 =-20 km ma in questo caso avremmo dovurto togliere il segno meno. Di conseguenza
la distanza tra Belpiano e Colnate è |50 - 30| km = 20 km .
Riprendiamo in maniera astratta questa idea.
Definizione 2.1 Sia (O,u,r) un riferimento cartesiano su una retta e siano A e B due punti su r di ascissa xA e xB rispettivamente. La distanza da A e B è
Estendiamo questa distanza alle coppie di punti del piano cartesiano
Siano A(1,2) e B(3,4) due punti del piano cartesiano.
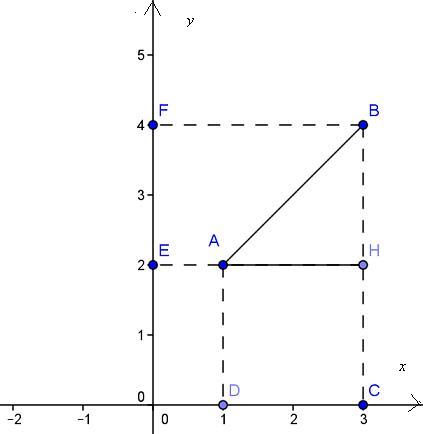
Il triangolo ABH è rettangolo on H. Di conseguenza, per il teorema di Pitagora
Per costruzione,
![]()
e siccome CD e EF stanno sulle rette dell'asse x ed y, si ha, per la Definizione 1.1
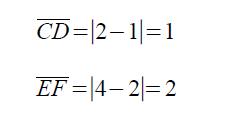
e quindi
![]()
questo calcolo si estende a una coppia di punti qualsiasi del piano cartesiano
Proposizione 2.1 Siano A(xA;yA) e B(xB;yB) due punti del piano cartesiano. Allora
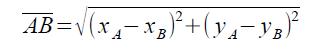
Nella vita quotidiana capita spesso di usare altre definizoni di distanza. La distanza di San Pellegrino Terme da San Giovanni Bianco, in linea d'aria, è data da Wolframalpha
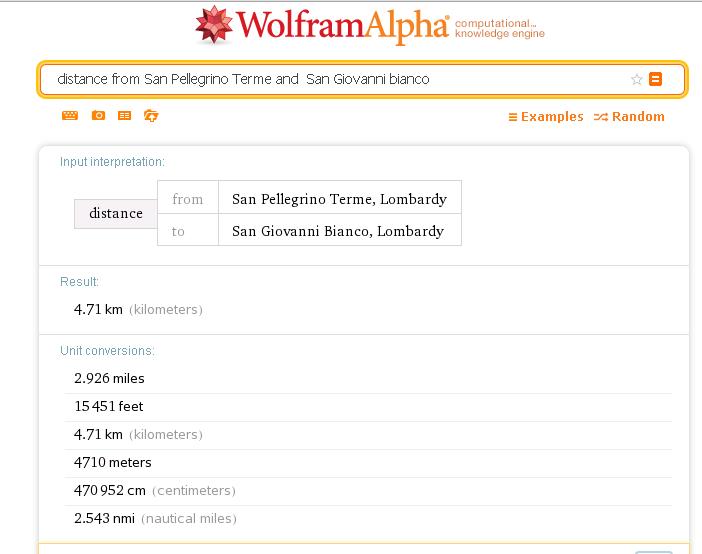
Secondo Wolframalpha, per andare da San Pellegrino a San Giovanni ci vogliono 3 minuti di automobile. Ma questo è palesemente falso, quindi è necessaria un'altra definizione di distanza, che tenga conto della strada che da San Pellegrino porta a San Giovanni
La distanza che si usa per i tragitti automobilistici è la distanza curvilinea
Siano A e B due punti del piano connessi
da una curva gamma. Si chiama distanza curvilinea di A da B la lunghezza dell'arco
AB lungo la curva gamma. Questa distanza si ottiene con strumenti matematici
che trasformano l'arco di curva in un segmento che ha la stessa lunghezza.
Il problema di trasformare curve e segmenti ha interessato da sempre i matematici.
I Greci tentarono in tutti i modi di risolverlo con la riga e il compasso-i
soli strumenti accettati da una cultura razionale come quella ellenica- e con
immensa sorpresa i loro fallimenti si trasformarono in un trionfo quando Isaac
Newton e i suoi contemporanei del 1600 crearono il calcolo
infinitesimale, uno strumento tanto potente quanto ricco di mistero-che
in diversi casi ci consente di trasformare una curva in un segmento.
Per calcolare il punto medio nel piano cartesiano, calcoliamo il punto medio tra due punti su una retta
In un piano cartesiano, siano A(1,0) e B(0,1). Ci proponiamo di trovare il punto medio del segmento AB. Il punto medio di AB è il pumto M tale che
Nella geometria euclidea, esiste una costruzione del punto medio con riga e compasso. Dato il segmento AB, con apertura di compasso maggiore dela metà di AB disegnamo l'arco di centro A e B. I punti C e D sono gli estremi dell'asse di AB. Pertanto, M è il punto medio cercato.
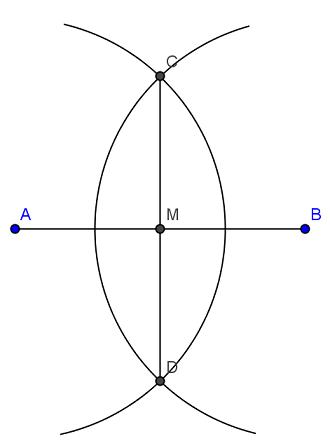
Eseguiamo la stessa costruzione in maniera analitica. Tracciamo i punti A e B e siamo Mx e My i punti medi di OA e OB, rspettivamente.
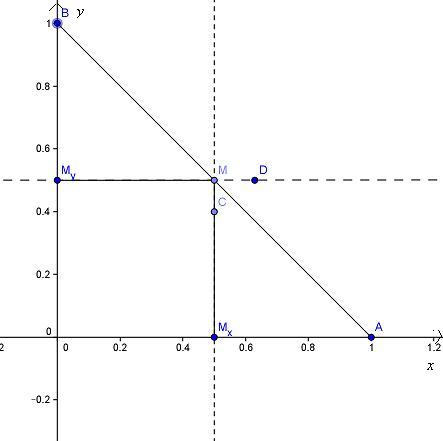
I triangoli AMxM e MMyB sono congruenti per il primo criterio di congruenza perchè
i) AMx è congruo a MMy per costruzione
ii) l'angolo BMMy è congruo all'angolo MxAM perchè corrispondenti nelle rette MyM e OA tagliate dalla trasversale AB
iii) l'angolo BMyM è congruo all'angolo MMxA perchè retto
Di conseguenza, AM è congruente ad MB.
Ne segue che le coordinate del punto M sono le ascisse dei punti medi di OA e OB. Ovvero
e quindi
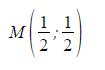
Possiamo affermare il seguente
Teorema 2.1 Siano A(xA,yA) e B(xB;yB) due punti del piano cartesiano. Allora il segmento AB ha come punto medio
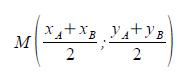
Il calcolo del punto medio di un segmento si estende al centro di massa di un insieme di punti nel piano cartesiano. Sia
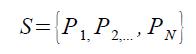
un insieme di N punti nel piano cartesiano, di coordinate (xi,yi), i=1...N. Le coordinate del suo centro di massa C sono
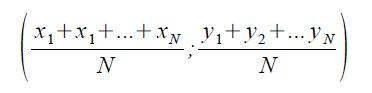
Il contenuto di questa pagina è interamente sotto la responsabilità dell'autore, Per segnalare imprecisioni ed errori, scirvere a ferrante.formato@istruzione.it .
Ultima modifica, 19 luglio 2015, ore 16.23
Domanda al professore a pagamento