6. Rette parallele

 

La geometrica analitica traduce propieta geometriche nel linguaggio dell'algebra. In questa sezione, applichiamo questo paradigma allo studio di due propieta geometriche: il parallelismo e la perpendicolarità

6.1 Spazi paralleli e spazi perpendicolari giustificazione del Quinto Postulato di Euclide.

 

Questa sezione è ispirata dal libro "Tentativi di Fondare la Matematica" del professor Giangiacomo Gerla , edizioni Feltrinelli

Nella geometria euclidea, il parallelismo tra rette è giustificato dal Quinto Postulato di Euclide. Le costruzioni della geometria analitica sono quindi un modello della geometria euclidea, come provato dal matematico A. Tarsky. E' ineterssante osservare che dai quattro postulati di Euclide si deriva comunque che

Fissata una retta r e un punto P esterno alla retta, esiste una retta parallela a r passante per P

Cominciamo a provare il seguente

Teorema 6.1 Un angolo esterno di un triangolo è sempre maggiore dei due angoli interni non adiacenti

Sia ABC un triangolo.

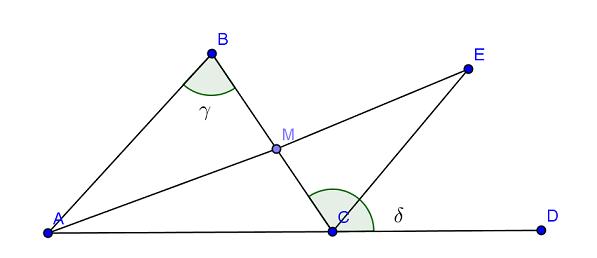
Sia l'angolo BCD. Costruiamo il punto medio di BC, indicato con M e prolunghiamo AM dalla parte opposta di BC per costruire il segmento EM congruente a AM. I triangoli AMB e EMC sono congruenti per il secondo criterio di congruenza -hanno gli angoli CME e BMA congruenti perchè opposti al vertice e i lati MC e ME congruenti rispettivamente a MB e AM per costruzione. Ne segue che gamma = BCE è più piccolo di BCD. Analogamente per BAC.

Teorema 6.2 Sia r una retta e P un punto esterno a r. Allora esiste una retta passante per P parallela as r

Sia la retta r, P un punto esterno ad r e S un punto di r. Tracciamo il segmento SP e indichiamo con delta uno degli angoli r e il segmento. SP. Per il punto P, tracciamo una retta s che forma con SP un angolo di ampiezza delta.

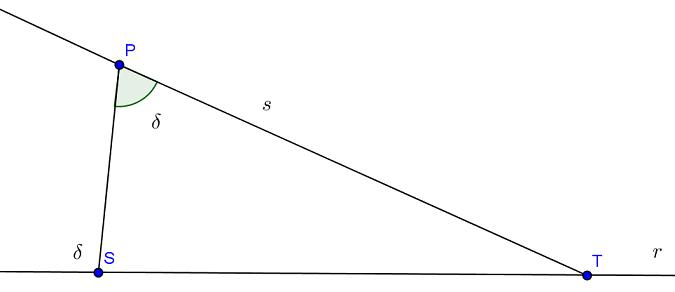
se per assurdo la retta s incontra la retta r in pun punto T, nel triangolo l'angolo esterno in S sarebbe uguale all'angolo interno SPT, ma questo è in contraddizione con il teorema precedente. Pertanto, la retta s è parallela a r.

Cerchiamo di ripetere questi concetti in maniera algebrica.

6.2 Equazione della retta passante per un punto fissato

Sia r una retta di equazione

y= mx+n

e sia P(1;1) un punto del piano. La retta r passa per P

1=m1+n=m+n

ovvero

1=m+m

dovrà essere quindi

y-1=mx+n-m-n =mx-m

ovvero

y-1=m(x-1)

e questa è l'equazione di una retta passante per P con coefficiente angolare m.

Di conseguenza vale il

Teorema 6.3 Sia P(x_A,y_A) un punto del piano cartesiano. La retta generica per P ha equazione

6.3 Condizioni di parallelismo tra due rette del piano cartesiano

Sappiamo che due rette sono parallele se non si incontrano mai. Nel piano cartesiano, due rette si intersecano quando le soluzioni dell'equazione di una retta sono anche soluzioni dell'equazione dell'altra retta. In altri termini, intersecare due rette vuol dire mettere a sistema le loro equazioni. Con questa osservazione, otteniamo le seguenti proprietà

Proposizione 6.1 Se due rette hanno lo stesso coefficiente angolare, esse sono parallele

dimostrazione. Siano due rette r ed s, entrambe non parallele all'asse y. Supponiamo che siano distinte. Allora le loro equazioni sono

e

con n diverso da n'.

Mettiamole a sistema e risolviamo con il metodo del confronto. Avremo che deve essere

da cui si ricava

ma questo è impossibile. Quindi non ci sono soluzioni e le due rette sono parallele. Se le sud erette coincidono, banalmente avranno lo stesso coefficiente angolare. Se le due rette sono parallele all'asse y il teorema è subito dimostrato, cossi' come se una delle due è parallela all'asse y. (QUED)

Vale anche il viceversa

Proposizione 6.2 Siano r ed r' due rette parallele. Allora hanno lo stesso coefficiente angolare.

Dimostrazione

Siano r ed r' due rette parallele di equazioni

 

e

Allora, il sistema di equazioni

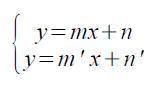
è impossibile. Questo sistema, con il metodo del confronto, è equivalente a

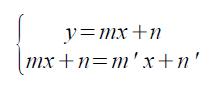
ovvero

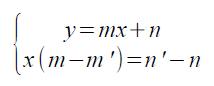
che è impossibile solo se la seconda equazione è impossibile, ovvero

da cui

Se una delle due rette è parallela all'asse y, la dimostrazione è immediata. (Q.E.D)

Que si due risultati sono riassunti dal seguente

Teorema 6.4 Due rette nel piano cartesiano sono parallele se e solo se hanno lo stesso coefficiente angolare

 

6.3 L'equazione di una retta passante per due punti

L'equazione di una retta passante per due punti si ottiene estendendo i risultati del Teorema 6.3. Siano A(1;1) e B(2;2) due punti distinti del piano cartesiano. Sappiamo che per A e B passa una sola retta. Determiniamo la sua equazione. Per il Teorema 6.3, la retta generica passante per il punto A ha equazione

(y-1)=m(x-1)

Tra le infinite rette che passano per A, determiniamo quella che passa per B. Dovrà essere

(2-1)=m(2-1)

 

e quindi il coefficiente angolare della retta per A e B è

m=1

a questo punto riscriviamo la (1) e otteniamo l'equazione

y-1=1*(x-1)

da cui

y-1=x-1

e quindi l'equazione della retta per A e B è

y=x

Abbiamo quindi il

Teorema 6.5 Siano A(x_A;y_A) e B(x_B;y_B) due punti distinti del piano cartesiano. L'equazione della retta passante per A e B è

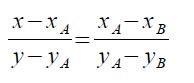
e il coefficiente angolare è

 

 

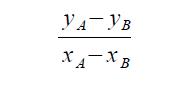
Il contenuto di questa pagina è interamente sotto la responsabilità dell'autore, Per segnalare imprecisioni ed errori, scrivere a ferrante.formato@istruzione.it .

Ultima modifica,27 luglio 2015, ore10.18