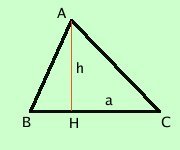
Area del triangolo Anche qui e' sufficiente fare riferimento al teorema sull'equiscomponibilita' fra parallelogramma e triangolo: Un triangolo e' equivalente ad un parallelogramma avente come base la stessa base e per altezza il doppio dell'altezza del parallelogramma quindi La misura dell'area del triangolo si ottiene dividendo a meta' il prodotto fra la misura della base e la misura dell'altezza As (ABC) = a·h -------- 2 Per memorizzarlo: base per altezza diviso 2 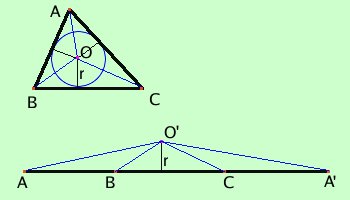Conoscendo il perimetro del triangolo ed il raggio del cerchio inscritto, per quanto visto nel capitolo sull'equivalenza, possiamo utilizzare la formula 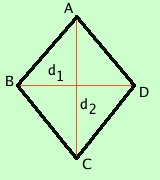La misura dell'area del triangolo si ottiene dividendo a meta' il prodotto fra la misura del perimetro e la misura del raggio del cerchio inscritto nel triangolo As (ABC) = 2p·r -------- 2 (a+b+c)·r = -----------------   2 Area del rombo Come conseguenza notevole troviamo l'area del rombo considerandola come l'area di due triangoli Infatti il rombo ABCD puo' essere pensato composto da due triangoli congruenti ABD e BCD, di base la diagonale d1 e con somma delle altezze la diagonale d2 quindi La misura dell'area del rombo si ottiene dividendo a meta' il prodotto fra la misura delle due diagonali As (ABCD) = d1·d2 -------- 2 Per memorizzarlo: diagonale per diagonale diviso 2

Geometria nel piano - Dino Betti

Scuola Elettrica

 

Altre applicazioni

Mappa per tipo di scuola

Indice di tutte le pagine del sito

Guida per navigare

Richiesta informazioni