Qui vediamo alcune definizioni ed anche una proprieta' notevole del triangolo isoscele:
|
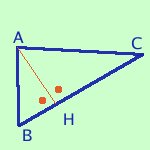
Definiamo altezza di un triangolo il segmento di perpendicolare condotto da un vertice al lato opposto
In figura AH e' un'altezza |
 |
|
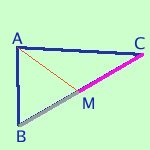
Definiamo mediana il segmento congiungente il vertice di un triangolo con il punto medio del lato opposto In figura AM e' una mediana |
 |
Date queste definizioni possiamo dire che vale
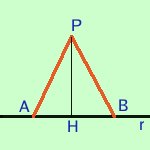
In un triangolo isoscele l'altezza, la mediana e la bisettrice condotte dal vertice opposto alla base sono coincidenti
Per esercizio fai la dimostrazione
e vale anche l'inverso
Se in un triangolo l'altezza, la mediana e la bisettrice condotte dal vertice opposto alla base sono coincidenti allora il triangolo e' isoscele
Per esercizio fai la dimostrazione
Siccome abbiamo un teorema ed anche il suo inverso d'ora in avanti i fatti
triangolo isoscele <=> altezza=mediana=bisettrice
saranno equivalenti
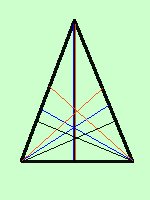
Naturalmente cio' vale solamente per il vertice e la base di un triangolo isoscele: negli altri due lati l'altezza, la mediana e la bisettrice saranno tre segmenti diversi
in figura:
altezze in nero
mediane in rosso
bisettrici in blu