E' il teorma inverso del precedente
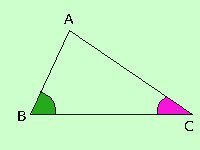Consideriamo un triangolo che abbia l'angolo ABC^ piu' grande ed l'angolo ACB^ piu' piccolo; dovremo dimostrare che, allora, il lato AC
č maggiore del lato ABPer fare il lato di fronte ad un angolo, ad esempio di fronte ad ACB basta che togli la lettera in mezzo C, ottieni AB
| ipotesi | tesi | |
| ABC^> ACB^ | AC > AB |
Neghiamo la tesi, se riusciamo a negare anche l'ipotesi allora il teorema e' vero
La tesi dice AC > AB Se non e' vera abbiamo due possibilita': o e' uguale o e' minore
- Non puo' essere AC = AB
perche' il triangolo avendo due lati uguali sarebbe isoscele ed avrebbe anche i due angoli uguali
cioe' ABC^= ACB^contro l'ipotesi - Nemmeno puo' essere AC <AB perche' se lo fosse, per il teorema precedente sarebbe ABC^< ACB^
contro l'ipotesi
