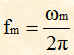
Indice di modulazione e potenza nella modulazione di ampiezza
Nella modulazione di ampiezza occorre considerare le ampiezze sia della modulante che della portante. Di solito l'ampiezza della modulante è circa il 40% dell'ampiezza della portante; è necessario, però, calcolare questa percentuale in modo da non causare distorsioni nel segnale modulato.
Indice di modulazione di ampiezza
Un generico segnale della modulante vm avente ampiezza o valore massimo Vm e frequenza fm:
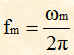
essendo in generale la pulsazione w=2pf, lo possiamo considerare sinusoidale e quindi esprimerlo con una equazione del tipo:
vm=Vm coswmt
Una generica portante vp avente ampiezza o valore massimo Vp e frequenza fp:
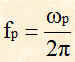
la possiamo considerare sinusoidale e quindi esprimerla con una equazione del tipo:
vp=Vp coswpt
Sappiamo che la frequenza della portante fp è maggiore della frequenza della modulante fp, quindi anche
wp>wp
Poniamo l'ampiezza della portante Vp maggiore dell'ampiezza della modulante Vm, cioè:
Vp>Vm
 |
|
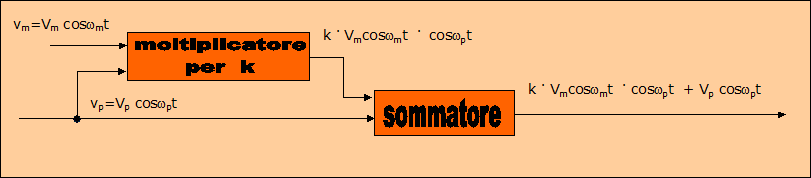
schema a blocchi di un modulatore in ampiezza |
Un circuito modulatore in ampiezza lo possiamo considerare composto da due stadi: un circuito moltiplicatore per k e un circuito sommatore.
Nel circuito moltiplicatore per k:
|
|
|
schema a blocchi di un moltiplicatore per k |
inviamo in ingresso la modulante:
vm=Vm coswmt
e la portante:
vp=Vp coswpt
In uscita otteniamo il prodotto dei due ingressi, cioè:
Vuk = k . Vmcoswmt . coswpt
 |
|
schema a blocchi di un modulatore in ampiezza |
Nel circuito sommatore inviamo l'uscita del moltiplicatore per k:
Vuk = k . Vmcoswmt . coswpt
e la portante:
vp=Vp coswpt
In uscita otteniamo la loro somma, cioè:
Vu = k . Vmcoswmt . coswpt + Vp coswpt
Poiché il termine:
coswpt
compare nei due addendi della somma lo mettiamo a fattore comune o in evidenza ed otteniamo:
Vu = ( Vp + k Vmcoswmt ) coswpt
Questa è l'equazione della forma d'onda modulata in ampiezza.
Si definisce indice di modulazione m il rapporto tra l'ampiezza della modulante diviso l'ampiezza della portante; poiché possiamo ritenere che la modulante sia stata moltiplicata per k, possiamo dire che l'indice di modulazione m è:
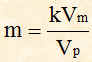
dove k è la costante di moltiplicazione del moltiplicatore, Vm è l'ampiezza della modulante, Vp è l'ampiezza della portante.
L'indice di modulazione m è un numero puro; se l'ampiezza della modulante è uguale a quella della portante,
m = 1
Di solito si preferisce un indice di modulazione pari a 0,4 ( 40% ) in modo che sia sempre la modulante più piccola della portante.
Alla pagina:
Applet modulazione di ampiezza (Agilent.com)
è possibile simulare come varia la modulazione al variare di m.
Possiamo misurare m in laboratorio con un oscilloscopio:
|
|
|
|
|
onda modulata in ampiezza |
possiamo vedere il valore massimo dell'onda modulata Vmax
Notiamo che:
Vmax = Vp + Vm
Indichiamo con Vmin l'ampiezza minima del segnale modulato:
Vmin = Vp - Vm
possiamo calcolare l'indice di modulazione m con la seguente formula:
![]()
Spettro dell'onda modulata in ampiezza
Riprendiamo l'equazione della forma d'onda di uscita:
Vu = ( Vp + k Vmcoswmt ) coswpt
Sviluppiamo i prodotti ed otteniamo:
Vu = Vp coswpt + k Vmcoswmt . coswpt
Consideriamo il fattore:
k Vm
e l'indice di modulazione m:
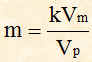
che possiamo scrivere:
m Vp = k Vm
Nella equazione:
Vu = Vp coswpt + k Vmcoswmt . coswpt
al posto di k Vm mettiamo m Vp ed otteniamo:
Vu = Vp coswpt + m Vp coswmt . coswpt
Al secondo termine dell'equazione compare il prodotto di due coseni:
coswmt . coswpt
in base alla formula di Werner:
cosa . cosb = ½ cos(a+b) + ½ cos(a-b)
lo possiamo trasformare come somma di due coseni; otteniamo:
coswmt . coswpt = ½ cos(wp+wm) t + ½ cos(wp-wm) t
La tensione modulata diventa quindi:
Vu = Vp coswpt + ½ m Vpcos(wp+wm) t + ½ m Vpcos(wp-wm)t
Questa equazione ci dice che l'onda modulata in ampiezza è la somma di tre segnali sinusoidali; la prima sinusoide è:
Vp coswpt
essa rappresenta la portante ed ha frequenza:
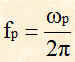
la seconda sinusoide è:
½ m Vpcos(wp+wm) t
rappresenta l'onda laterale superiore ed ha frequenza:
fp+fm
la terza sinusoide è:
½ m Vpcos(wp-wm) t
rappresenta l'onda laterale inferiore ed ha frequenza:
fp - fm
|
|
|
spettro generico di un'onda modulata in ampiezza |
Se l'indice di modulazione m =1 le due onde laterali hanno ampiezza uguale alla metà dell'ampiezza della portante.
|
|
|
spettro con portante di 500 kHz , modulante di 20 kHz, indice di modulazione m=1 |
Notiamo che l'informazione non è contenuta nella portante ma in ciascuna delle due onde laterali, per cui la portante può anche essere soppressa per risparmiare potenza nel tramettitore.
Potenza nella modulazione di ampiezza
La formula della potenza in generale è la seguente:
P = V I
dove V è la tensione in valore efficace.
Poiché Vp è il valore massimo della portante, il valore efficace della tensione della portante è:
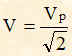
mentre la corrente I in valore efficace è:
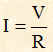
dove R è il valore di resistenza del carico, rappresentato dall'antenna; di conseguenza la potenza della portante Pp ha la formula:
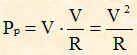
che è la potenza della sola portante.
Vi sono inoltre le due potenze delle onde laterali, quella inferiore e quella superiore; ciascuna onda laterale ha un valore massimo di tensione:
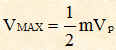
di conseguenza la potenza di ciascuna onda laterale PL sarà uguale a quella della portante Pp moltiplicata per:
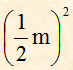
cioè:
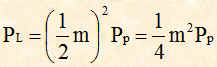
La potenza totale PT è:
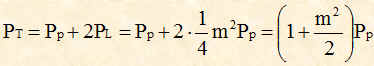
Da questa formula vediamo che la potenza delle due onde laterali è molto piccola rispetto a quella della portante.
Esercizi sulla modulazione in ampiezza
| Domanda al professore |
2009