Resistores en serie y paralelo

Resistores en serie

Dos o más resistores están conectados en serie cuando son la misma corriente. Ejemplo:


circuito con dos resistores en serie	vista de dos resistores conectados en serie

Tomamos nota de que la corriente a través del resistor R₁también debe ir del resistor R₂ , como el punto de unión entre R₁ y R₂ no hay otros componentes; se dice que están conectados en serie. Este tipo de conexión es necesaria cuando se quiere obtener voltajes más bajos que la tensión de alimentación del circuito. Para calcular la resistencia total de las dos resistores, vista desde los terminales A y B , es decir, R_T, se utiliza la siguiente fórmula:

R_T= R₁+ R₂

La resistencia total R_t también podemos indicar cómo la resistencia equivalente R_eq , es decir, las dos resistencias tienen el mismo valor de una única resistencia que tiene como resistencia a la suma de las resistencias de los dos resistores.

Si hay más de dos resistores utilizando la fórmula:

R_T= R₁+ R₂+ R₃+ ……

En última instancia para obtener la resistencia total se convierte en la suma de los valores de todos los resistencias conectadas en serie.

Ejercicios de resistores

Resistores en paralelo

Dos o más resistores están conectados en paralelo cuando los terminales respectivos están conectados uno con el otro de modo que el voltaje aplicado es el mismo. La conexión en paralelo es más utiliza, de hecho, en una carcasa común todos los equipos eléctricos están conectados en paralelo. El esquema eléctrico la siguiente.


circuito con dos resistores en parallelo	vista de dos resistores conectados en parallelo

Para calcular la resistencia total usando la fórmula siguiente :

             R_T =                          1                         ..
                             1     +       1      +       1     .
                             R₁R₂R₃ .

Cuando los resistores son dos lata utilice la siguiente fórmula:

R₁x R₂

R_T = -------------------
R₁ + R₂ .

Ejercicios de resistores

Corso di Elettronica

GENERADOR DE TENSIÓN IDEAL Y REAL

Por lo general, en un generador de tensión común pueden observar dos fenómenos particulares. Un primer fenómeno se refiere a la calefacción del generador durante el uso. Un segundo problema se refiere a la disminución de la tensión a medida que aumenta la corriente suministrada por el generador. Para tener en cuenta estos fenómenos se distingue entre el generador ideal y real del generador.

Se dice generador ideal de un generador que mantiene su tensión en sus terminales, incluso si la corriente aumenta o disminuye, es decir la tensión no depende de la corriente. El generador ideal de curso no existe en la naturaleza. El esquema es la siguiente:

Generatore di tensione ideale, perché privo di resistenza interna

Generador de tensión ideal, que carece de resistencia interna

El generador de tensión ideal tiene la misma tensión para variar corriente.

tensión del generador ideal para variar de la corriente

Yo recuerdo que estamos hablando de los generadores tensión continua, es decir, un generadores de tensión que tienen constante en el tiempo, tales como baterías y pilas .

Característica del generador de tensión continua para variar el tiempo

El verdadero generador, es decir, lo que realmente existe en la naturaleza, lo representamos con el siguiente esquema:

Generador de tensión real

Este esquema es obtenido mediante la inserción de un generador ideal con una resistencia R_i . Cabe señalar que la resistencia R_i no existe, pero el verdadero generador implica en todos los aspectos como si tuviera dentro de un resistor. La resistencia R_i es una resistencia interna que tiene en cuenta la caída de tensión a los cambios de la corriente y el calentamiento del generador de tensión. De hecho, cuando aumenta la corriente a través de R_i es un caída de tensión se puede calcular con la ley de Ohm:

V_i = R_i I _i

por lo tanto, la mayor la corriente mayor la caída de tensión en la resistencia interior. El voltaje a través de la resistencia interna de la llamada caída de tensión debido disminuye el valor de la tensión del generador. De hecho, la tensión presente en los terminales A y B es dada por

V_AB = E - V_i

Dónde V_AB es el voltaje de salida del generador, E es la fuerza motriz electro de generador ideal, V_i es la caída de tensión a través de la resistencia R_i.

Curso de la tensión para variar la corriente, en un generador real

Tomamos nota de que en el generador real de la tensión presente en los terminales es menor que la fuerza electromotriz; En particular, es dicha fuerza electromotriz de un generador que la tensión generada por ella, pero no lo es disponible en los terminales; la fuerza electromagnética de conducción coincide con el generador de tensión ideal, y denota con la letra E. En cambio, se dice que el verdadero poder de un generador de tensión disponible en las terminales; es menor que la fuerza electromotriz E. La tensión en los bornes denotan por V_AB .

Tensión en vacío

Si un generator de tensión real no sumistra corriente, que dice que está a vacío .

Generatore di tensione reale

Generator de tensión en vacío porque entre A y B hay no resistors

Cuando un generador es vaciar la tensión en los bornes coincide la fuerza electromotriz, ya que hay caída de tensión en la resistencia interior.

hecho de que la ley de Ohm que haría

V_i = R_i I_i = R_i x 0 = 0 V

En consecuencia, la tensión de los terminales trai A y B se convierte:

V_AB = E - V_i = E - 0 = E

De esta ecuación podemos ver como con el aumento de la corriente de salida, ya que aumenta la V_i debe disminuir la tensión en los terminales V_AB . La tendencia V_AB es del tipo lineal, es decir, disminuye siguiendo una línea recta, ya que aumenta la corriente de salida I_i.

Cortocircuito

El cortocircuito es la situación que se obtiene cuando se combinan los dos terminales de un generador por medio de uno hilo conductor.

generador real en cortocircuito (para evitar)

En esta situación, el generador se ve obligado para proporcionar la corriente máxima posible; esta situación es extremadamente peligrosa en que el conductor de cobre exterior se recalienta hasta que el fusión rápida, con el tema de material incandescente; Además, también la generador se sobrecalienta, hasta la explosión. Para evitar que accidentalmente peligrosa situación ocurre, cada generador está protegido a través de un fusible .

El fusible está hecho de un alambre de material conductor delgado que se coloca dentro de un recipiente en vidrio.

Fusible a hilo

El fusible está conectado en serie a circuito a ser protegidos.

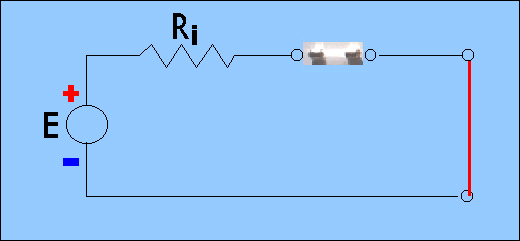Generador protegido con fusible

En la hipótesis de que hay un corto circuito en los terminales del generador, el alambre fusible se funde en primer lugar, en ya que es muy fina; su fusión, sin embargo, no es peligroso, ya se produce dentro de un recipiente de vidrio. El derretimiento de los cortes de fusibles el circuito, como si se tratara de un interruptor, para lo cual se impide el paso de la corriente, ya que el circuito está abierto.

El fusible debe tener un valor de corriente adecuado, que corresponde a la máxima prevista para el circuito.

GENERATORES DE TENSIÓN EN SERIE Y PARALELO

Para conectar en serie los generadores de tensión mediante el siguiente diagrama eléctrico:

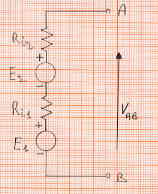
Due generatori di tensione collegati in serie

Tomamos nota de que la tensión total disponible en los terminales será la suma de las dos tensiones, es decir:

V_AB = E₁ + E₂ - V_i1- V_i2

Donde V_ABes el tensión disponible en los terminales, E₁ es la fuerza electromotriz del primer generador, E₂ es la fuerza electromotriz del segundo generador, V_i1 es la caída de tensión en la resistencia interna del primer generador, V_i2 es la caída de tensión en la resistencia interna de lo segundo generador.

La conexión en paralelo de dos generadores se lleva a cabo de acuerdo con el siguiente diagrama eléctrico:

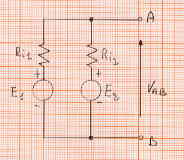
Due generatori di tensione collegati in parallelo

Cabe señalar que para evitar el sobrecalentamiento de los generadores con la pérdida de la energía requiere que los dos generadores tienen la misma fuerza electromotriz que es E₁ = E₂, y también debe tener la misma resistencia interna, es decir, R_i1 = R_i2, de modo que la tensión disponible en los bornes sea igual, es decir

V_AB = E₁ - V_i1= E₂ - V_i2

Si estas dos condiciones no son se reunió la conexión en paralelo no es posible, ya que una gran proporción la energía sería absorbida por el generador con tensión menor.

PRINCIPIO DE KIRCHHOFF DE LAS CORRIENTES LCK

Dado un circuito genérico:

I resistori R2 ed R3 sono collegati in parallelo tra di loro, ed in serie ad R1

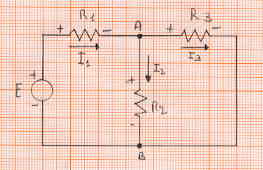
se dice nodo un punto del circuito donde se conectan al menos tres componentes. Se dice malla una trayectoria cerrada que se obtiene a partir de un nodo y volver al mismo nodo. Se dice lado una parte lateral del circuito entre dos nodos. En nuestro caso hay dos nodos, un nodo A y un nodo B. Hay tres mallas:

Malla 1: comprende los componentes E, R1,R2

Malla 2: comprende R2,R3

Malla 3: comprende E,R1,R3

También deben establecerse para cada nodo de la dirección de las corrientes, que puede ser elegidos a voluntad, sólo si el resultado de la voluntad de cálculo. Un número positivo significa que la dirección elegida es la correcta, si el resultado será un número negativo significa que la dirección elegida es mal y por lo tanto debe ser revertida.

Nodo A

Denotamos por I₁ la corriente entrante en el nodo A y que se ejecuta a través los componentes E y R₁ ; denotamos por l₂ la corriente que sale del nodo A y se ejecuta a través de la resistencia de R₂ ; denotamos por l₃ la corriente que sale del nodo A y se ejecuta a través de la resistencia de R₃ .

El principio de Kirchhoff de las corrientes dice que en cualquier nodo la suma de las corrientes entrantes es igual a la suma de las corrientes salientes.

En el nodo A la fórmula es la siguiente:

I₁= I₂+ I₃

Este principio se utiliza para calcular una corriente cuando se conocen las otras. También nos dice que en el nodo la corriente no se pierde, pero toda la corriente que entra en el nodo la hallamos a la salida.

PRINCIPIO DE KIRCHHOFF DE LAS TENSIONES LVK

El principio de las tensiones se aplica a cualquier malla de el circuito.

Circuito con due maglie interne ed una esterna

Una vez marcado en las corrientes de cortocircuito necesidad de poner los signos de las tensiones de cada componente de esta manera: el lado que la corriente entra en el componente que poner un signo + y desde el lado de poner un signo - , por tanto, por lo que sabemos la dirección de la caída de tensión a través de cada componente. Sin esto, se selecciona una dirección de desplazamiento de una malla arbitraria.

El principio de tensiones de Kirchhoff dice que en cualquier malla la suma algebraica de las fuerzas electromotrices es igual a la suma algebraica de las caídas de tensión de los otros componentes de la malla.

Cabe señalar que los generadores se deben tomar con un signo positivo si navegar la malla se encuentra con el primer signo - y luego el signo + ; en cambio, los resistores se deben tomar con el signo + si cumple con el primer signo + y luego el signo - ; se debe tomar con el signo - si cumple antes de la - y entonces el + .

En particular, si se considera la primera malla constituida por E, R₁, R₂ obtenemos:

E = V₁ + V₂

Dónde E es la tensión del generador, V₁ la tensión en los bornes de R₁, V₂ es la tensión en los bornes de R₂.

Por la segunda malla constituida por R2,R3obtenemos:

0 = V₃ - V₂

Dónde 0 es la tensión de los generadores, de hecho no hay generadores, V₃ es la tensión en los bornes de R₃, V₂ es la tensión en los bornes de R₂; esta tensión se debe tomar con signo - porque en navegando la malla se reúne antes el - e poi il +.

Por la tercera malla constituida por E,R1,R3 obtenemos:

E = V₁ + V₃

Dónde E es la tensión de el generador, V₁ es la tensión en los bornes de R₁, V₃ es la tensión en los bornes de R_3.

Ejercicio

Verifique el principio de actual en todos los nodos del circuito.

Compruebe la segunda de suéteres en todas las mallas del circuito.

Circuito con due maglie interne ed una esterna

E = 12 V

R₁ = 0,1 W

R₂ = 20 W

R₃ = 20 W

diagrama eléctrico

datos conocitosi

Primero debe calcular todas las tensiones y todas las corrientes del circuito y compruebe los dos principios de Kirchhoff .

Desde los dos resistores R₂ y R₃ son en paralelo calculamos la resistencia equivalente R_p:

R_p =                             1                       =
                             1      +       1     .
                    R₂R₃ .

=                1                       = 10 W
              1      +       1     .
      2020 .

Sustituyendo los dos resistores R₁ y R₂ su paralelo R_p, el circuito se convierte en:

Circuito equivalente a lo inicial

Calculamos ahora la resistencia total; tomamos nota de que R₁ y R_p están en serie, por lo que su resistencia equivalente a la siguiente:

R_t = R₁+ R_p = 0,1 + 10 = 10,1 W

El circuito ahora es el siguiente:

Circuito equivalente a lo inicial

Por que la ley de Ohm calcular la corriente total del circuito.

V_t= R_tx I_t

I_t =             Vt      =    12      = 1,1881 A
Rt         10,1

La corriente total fluye en la resistencia total R_t .

Reconsideremos ahora el circuito equivalente anterior:

Circuito equivalente a lo inicial

La corriente será igual en todos los componentes del circuito y en particular en R₁ y R_p. Por lo tanto, podemos escribir:

I₁ = I_p = I_t = 1,1881 A

En este punto podemos el cálculo de las dos tensiones en los extremos de R₁ y en los cabos de paralelo R_p , utilizando la ley de Ohm. Obtenemos entonces:

V₁= R₁x I₁= 0,1 x 1,1881 = 0,11881 V

mientras por V_p obtenenos:

V_p= R_px I_p= 10 x 1,1881 = 11,881 V

Pero desde R_p es el paralelo de los dos resistores R₂ y R₃, y sabiendo que las resistencias en paralelo tienen la misma tensión, podemos escribir:

V₂=V₃=V_p= 11,881 V

La aplicación de Ahora la fórmula inversa de la ley de Ohm podemos calcular las dos corrientes:

I₂ = V₂ = 11,881 = 0,5940 A
R₂ 20

Del mismo modo por I₃ obtenemos:

I₃ = V₃ = 11,881 = 0,5940 A
R₃ 20

Conociendo, ahora, todas las corrientes y todas las tensiones, podemos verificar la primera ley de Kirchhoff en el nodo A, y o sea:

I₁= I₂+ I₃

1,1881= 0,590 + 0590

1,1881 = 1,188

Podemos decir que la primera principio se satisface en el nodo A . La diferencia entre 1,1881 y 1,188 es debido al hecho de que en los cálculos es, por desgracia, pasar por alto algunos lugares decimales.

En lo nodo B tenemos

I₂+ I₃= I_G

donde I_G es la corriente del generador que sea igual a la corriente total que se

I_G = 1,1881 A

La ecuación en el nodo B se convierte:

0,590 + 0590 = 1,1881

1,188 = 1,1881

Podemos decir que lo primero principio se cumple en el nodo B. La diferencia entre 1,1881 y 1,188 es debido al hecho de que en los cálculos es, por desgracia, pasar por alto algunos lugares decimales.

La verificación del principio de las mallas

Consideremos la primera malla:

E = V₁ + V₂

Fijemos una línea de caminando hacia la derecha, ponen los signos + y - junto a cada resistor. Veamos primero la suma de todos los generadores de tensión presentes, entonces esa es la que es E; lo tomamos con el signo + , ya que se reunió antes de la -. Incluso las dos tensiones V₁ y V₂ llevarlos con el signo + , porque para las resistencias, el signo es concordante; a continuación la ecuación de la primera malla será :

E = V₁ + V₂

12 = 0,11881 + 11,881

12 = 11,99981

El segundo principio de las mallas se cumple por primera malla, excepto las aproximaciones decimales.

Por la segunda malla tenemos:

0 = - V₂+ V₃

Puesto que hay generadores tensión, que significa que su suma es igual a cero; la tensión V₂ será negativa, ya que nos encontramos con los primeros el - entonces el + ; mientras que la tensión V₃ será positiva.

Entonces la ecuación de la segunda malla es:

0 = - V₂ + V₃

0 = -11,881 + 11,881

0 = 0

Por esta malla el principio de las tensiones está satisfecho.

Recuerde el última malla externa:

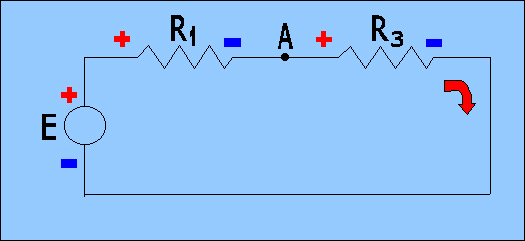E = V₁ + V₃

Veamos primero la suma de existen todos los generadores de tensión, entonces eso es una que es E ; lo tomamos con el signo + , desde que nos conocimos antes de que el signo - . Incluso el dos tensiones V₁ y V ₃ llevarlos con el signo + , porque para los resistores, el signo es concordante; a continuación la ecuación de la tercera malla será :