Teorema dell'angolo esterno

Teorema dell'angolo esterno
Enunciato:
In ogni triangolo un angolo esterno e' maggiore di ogni angolo interno non adiacente
che cos'e' un angolo esterno nota bene!
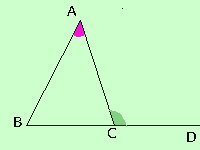Consideriamo come angolo interno l'angolo BAC^ e come angolo esterno l'angolo ACD^

ipotesi tesi

ACD^ esterno ACD^ > BAC^

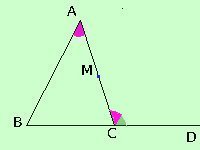
Per dimostrare che un angolo e' maggiore di un'altro basta prenderne una parte e mostrare che la parte e' uguale all'altro angolo, quindi dovremo costruire due triangoli, uno con l'angolo interno e l'altro con la parte dell'angolo esterno

ti faccio la costruzione passo-passo.

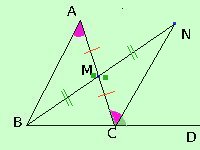
Considero il punto medio M del lato AC

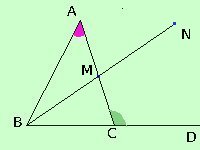
Ora considero il segmento BM e riporto un segmento uguale sul prolungamento di BM oltre M, ottengo il segmento MN

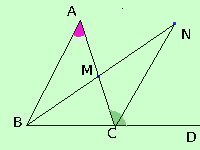
congiungo N con C e considero i triangoli ABM ed MNC

essi hanno
AM = MC per costruzione
BM = MN sempre per costruzione
gli angoli AMB^ = NMC^ perche' opposti al vertice
Per il primo criterio di congruenza i due triangoli sono congruenti, in particolare BAM^= MCN^ ed essendo MCN^ una parte dell'angolo ACD^ si avra' la tesi
Una volta studiato, per vedere se hai capito bene, prova a dimostrare il teorema considerando altri angoli