La tesi e' che AF e' la bisettrice dell'angolo A quindi che gli angoli BAF e FAC sono congruenti
per dimostrare che sono congruenti i due angoli devo considerare due triangoli di cui facciano parte BAF e FAC e vedere se sono congruenti:
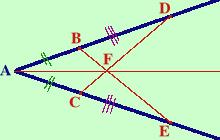
- Considero i triangoli BAF e FAC so che hanno uguali AB ed AC per ipotesi ed inoltre hanno AF in comune, mi manca un altro lato (un angolo non va bene perche' devo dimostrare che e' congruente proprio l'angolo compreso), quindi devo considerare due altri triangoli
- Provo a considerare i triangoli DAF e EAC so che hanno congruenti AD ed AE (perche' somma di segmenti congruenti) ed inoltre hanno AF in comune, mi manca un altro lato (anche qui l'angolo non va bene per lo stesso motivo precedente), quindi devo considerare due altri triangoli (allora tanto vale procedere con i triangoli precedenti)
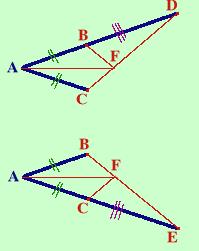
Passo a considerare i triangoli DAC e BAE perche' hanno come angoli gli angoli precedenti (te li estraggo in una figura a parte)
I triangoli DAC e BAE hanno l'angolo A in comune, poi AB congruente ad AC per ipotesi ed AD congruente ad AE perche' somma di segmenti congruenti; vale quindi il primo criterio
















