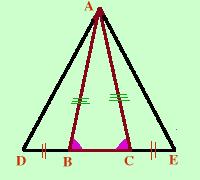
Ora facciamo il ragionamento contrario del punto precedente: cioe' partiamo dalle ipotesi ed arriviamo alla tesiConsidero i triangoli ABD ed ACE, essi hanno:
AB=AC per ipotesi
BD=CE per costruzione
gli angoli DBA=ECA perche' angoli supplementari di angoli congruenti
Quindi i due triangoli sono congruenti per il primo criterio di congruenza ed in particolare saranno congruenti AD e AE
Il triangolo ADE, avendo due lati congruenti, e' isoscele come volevamo dimostrare
Ora mettiamo tutto assieme ed abbiamo il risultato finale
