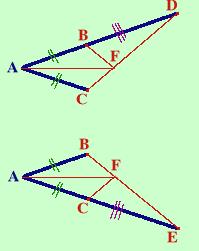
Scriviamo lo stesso procedimento a rovescio

Scriviamo lo stesso procedimento a rovescio(partiamo dall'ipotesi ed arriviamo alla tesi)

Ora facciamo il ragionamento contrario del punto precedente: cioe' partiamo dalle ipotesi ed arriviamo alla tesi
Considero i triangoli ADC ed ABE (te li ho estratti dalla figura completa), essi hanno:

AC=AB per ipotesi
AD=AE perche' somma di segmenti congruenti
L'angolo A in comune

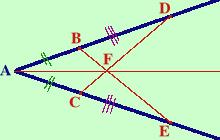Quindi i due triangoli sono congruenti per il primo criterio di congruenza ed in particolare saranno congruenti gli angoli ADC=AEB e ABE=ACD

Considero ora i triangoli BFD e CFE, essi hanno:

BD=CE per ipotesi
Gli angoli BDF=CEF perche' appena dimostrato Corrispondono agli angoli ADC ed AEB
Gli angoli FBD=FCE perche' supplementari degli angoli congruenti ABE=ACD come abbiamo appena dimostrato Supplementari vuol dire che con gli altri angoli formano un angolo piatto

I due triangoli sono congruenti per il secondo criterio ed in particolare hanno congruenti i lati BF=CF
Considero infine i triangoli ABF e ACF, essi hanno:

AB=AC per ipotesi
I lati AF congruenti perche' in comune
BF=CF perche' appena dimostrato

Quindi i due triangoli sono congruenti per il terzo criterio ed in particolare avranno congruenti gli angoli BAF=CAF cioe' AF
e' la bisettrice come volevamo dimostrare

Ora mettiamo tutto assieme ed abbiamo il risultato finale

Geometria nel piano - Dino Betti

Inferiore betti