Il parallelogramma e il rettangolo insieme

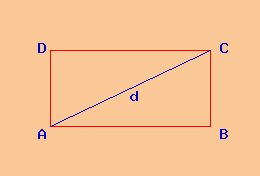
rettangolo	parallelogramma

I problemi riportati sono più di 600; occorre ricordare che questo è un programma di intelligenza artificiale, cioè la soluzione non si basa su di un archivio di problemi svolti, ma si basa su di un algoritmo, cioè un modulo o una parte del programma del calcolatore geometrico, che esamina la traccia del problema e cerca una soluzione, seguendo le regole della geometria che si insegna a scuola.

Il programma automatico esamina i dati forniti; per esempio seguiamo lo svolgimento della seguente traccia:

Un rettangolo ha la base di 50 cm e l'altezza 4/5 della base. Calcola l'area di un parallelogramma isoperimetrico al rettangolo e avente l'altezza di 20 cm e la base congruente all'altezza del rettangolo.

Il programma esamina la prima parte della traccia:

Un rettangolo ha la base di 50 cm e l'altezza 4/5 della base.

e riscontra che i dati forniti sul rettangolo sono completi, cioè del rettangolo si possono calcolare sia la base, sia l'altezza, sia le diagonali, sia il perimetro, sia l'area, ecc.

Invece del parallelogramma viene fornita solo l'altezza che è 20 cm:

Calcola l'area di un parallelogramma isoperimetrico al rettangolo e avente l'altezza di 20 cm e la base congruente all'altezza del rettangolo.

Per ricavare le altre dimensioni il programma analizza tutta la traccia e cioè gli altri dati impliciti del parallelogramma che sono il perimetro e la base. Analizza la parola isoperimetrico e ne deduce che occorre calcolare il perimetro del parallelogramma che è congruente a quello del rettangolo e quindi dice:

isoperimetrico vuol dire che il perimetro del parallelogramma = perimetro del rettangolo.
 

Il programma va, quindi, a calcolare il perimetro del rettangolo e si accorge che manca la misura dell'altezza, che nel nostro caso è 4/5 della base; per cui si va a calcolare i 4/5 della base e dice:

Calcolo altezza del rettangolo sapendo che:
base del rettangolo = 50 cm
rapporto = 4/5
Applico la formula:
altezza del rettangolo = base del rettangolo x rapporto ed ottengo:
altezza del rettangolo = 50 cm x 4/5 = 40 cm

Risposta
altezza del rettangolo è 40 cm
 

A questo punto, sapendo base e altezza del rettangolo si può calcolare il perimetro, in quanto sappiamo sia la base che l'altezza del rettangolo.

Il programma, quindi, continua e ci dice:

Dati
Poligono: rettangolo ABCD
base b = 50 cm
altezza h = 40 cm

Soluzione

Si richiede il perimetro del rettangolo ABCD i cui lati sono:
AB = 50 cm.
BC = 40 cm
Applico la formula:
p = AB + BC + CD + DA
ed ottengo:
p = 50 cm + 40 cm + 50 cm + 40 cm = 180 cm

Risposta
Il perimetro del rettangolo ABCD è 180 cm.
 

Notiamo che il disegno del rettangolo viene fatto in scala, cioè rispettando le proporzioni tra base e altezza. Ricavato il perimetro del rettangolo il programma deduce che anche il parallelogramma ha il perimetro di 180 cm; infatti continua dicendo:

Il perimetro del parallelogramma è 180 cm
 

A questo punto del parallelogramma sappiamo il perimetro che è 180 cm, l'altezza che è 20 cm, ma dovendo calcolare l'area ci serve comunque la base del parallelogramma che ancora non sappiamo; sappiamo però che:

la base congruente all'altezza del rettangolo.

Essendo l'altezza del rettangolo pari a 40 cm, il programma ci dice:

La base del parallelogramma misura 40 cm.
 

Ora abbiamo tutti gli elementi per calcolare l'area, in quanto sappiamo sia la base che l'altezza del parallelogramma; per cui il programma prosegue e ci dice:

Dati
Poligono: parallelogramma ABCD
base b = 40 cm
altezza h =20 cm

Soluzione

Si richiede l'area di un parallelogramma ABCD avente:
base b = 40 cm
altezza h =20 cm
Applico la formula:
A = b x h ed ottengo:
A = 40 cm x 20 cm = 800 cm²

Risposta
L'area del parallelogramma ABCD è 800 cm².
 

Qui il disegno è in scala per quanto riguarda la base e l'altezza; ma non per il lato obliquo, che non è stato calcolato, in quanto non richiesto dal problema.

Volendo ottenere altri dati sul parallelogramma occorre usare una password, che si ottiene mediante il pagamento; per esempio se voglio lato obliquo e diagonali del parallelogramma posso modificare la traccia in questo modo:

Un rettangolo ha la base di 50 cm e l'altezza 4/5 della base. Calcola le diagonali di un parallelogramma isoperimetrico al rettangolo e avente l'altezza di 20 cm e la base congruente all'altezza del rettangolo.

Questa traccia non figura tra i problemi segnalati come risolvibili; tuttavia il programma la risolve comunque. Questo per dire che i problemi risolvibili sono molti di più di quelli riportati in questa pagina del parallelogramma e rettangolo insieme. Infatti otteniamo:

Dati
Poligono: parallelogramma ABCD
perimetro p = 180 cm
base AB = 40 cm

Soluzione

Si richiede il secondo lato BC del parallelogramma ABCD il cui perimetro p = 180 cm e la cui base è AB = 40 cm
Applico la formula:
perimetro p = 2 base + 2 lato obliquo
da cui ricavo:
2 lato obliquo = p - 2 x base
da cui ricavo:
lato obliquo BC =
lato obliquo BC = = 50 cm


Risposta
Il lato obliquo BC del parallelogramma ABCD è 50 cm
 

Cioè, dal perimetro, conoscendo la base, si è calcolato il lato obliquo; poi il programma prosegue calcolando le diagonali; infatti otteniamo:

Dati:
Poligono: triangolo rettangolo HDA
cateto c = HD = 20 cm
ipotenusa a = DA = 50 cm

Soluzione

Si richiede un cateto di un triangolo rettangolo HDA avente:
cateto c = HD = altezza del parallelogramma = 20 cm
ipotenusa a = DA = lato obliquo = 50 cm

Applico la formula derivata dal teorema di Pitagora:

cateto b = AH = segmento AH = V a² - c² ed ottengo:

cateto b = V(50 cm)² - (20 cm)² = 45,825756949558 cm

Risposta
L'altro cateto b = AH del triangolo rettangolo HDA, che coincide con segmento AH, è 45,825756949558 cm.

Si richiede segmento HB sapendo che:
base = 45,825756949558 cm
segmento AH = 40 cm
Applico la formula:
segmento HB = base - segmento AH ed ottengo:
segmento HB = 45,825756949558 cm - 40 cm = 5,825756949558 cm

Risposta
segmento HB è 5,825756949558 cm


Dati:
Poligono: triangolo rettangolo HBD
cateto b = DH = 20 cm
cateto c = HB = 5,825756949558 cm

Soluzione

Si richiede l'ipotenusa di un triangolo rettangolo HBD avente:
cateto b = DH = altezza = 20 cm
cateto c = HB = proiezione HB della diagonale minore = 5,825756949558 cm
Applico la formula del teorema di Pitagora:
ipotenusa a = BD = V b² + c² ed ottengo:
a = V(20 cm)² + (5,825756949558 cm)² = 20,831213215637 cm

Risposta
L'ipotenusa del triangolo rettangolo HBD, che coincide con diagonale minore BD, è 20,831213215637 cm.

Dati
base = 40 cm
segmento AH = 45,825756949558 cm

Risposta

Si richiede segmento AH' sapendo che:
base = 40 cm
segmento AH = 45,825756949558 cm
Applico la formula:
segmento AH' = base + segmento AH
ed ottengo:
segmento AH' = 40 cm + 45,825756949558 cm = 85,825756949558 cm

Risposta
segmento AH' è 85,825756949558 cm


Dati:
Poligono: triangolo rettangolo H'CA
cateto b = AH' = 85,825756949558 cm
cateto c = H'C = 20 cm

Soluzione

Si richiede l'ipotenusa di un triangolo rettangolo H'CA avente:
cateto b = AH' = segmento AH' = 85,825756949558 cm
cateto c = H'C = altezza = 20 cm
Applico la formula del teorema di Pitagora:
ipotenusa a = CA = V b² + c² ed ottengo:
a = V(85,825756949558 cm)² + (20 cm)² = 88,12525492709 cm

Risposta
L'ipotenusa del triangolo rettangolo H'CA, che coincide con diagonale maggiore AC, è 88,12525492709 cm.
 

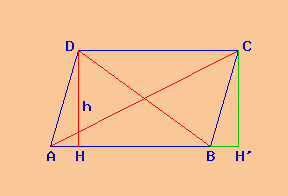
Notiamo la complessità di calcolo delle due diagonali; infatti il programma dapprima disegna in scala sia l'intero parallelogramma che le due diagonali; poi si calcola il segmento AH con il teorema di Pitagora ed ottiene AH = 45, 82 cm.

Poi toglie la base dal segmento AH ed ottiene la misura del segmento HB = 5,82 cm

Applica il teorema di Pitagora tra segmento HB e altezza e ottiene la diagonale minore BD = 20,83 cm.

Per calcolare la diagonale maggiore ci serve la misura del segmento AH' che si ottiene aggiungendo la base al segmento AH; quindi segmento AH' = 85,82 cm

Poi con Pitagora si ottiene la diagonale maggiore AC = 88,12 cm

Scuola Elettrica

Scuola Elettrica