7. Rette perpendicolari
A differenza del parallelismo, la nozione di perperndicolarità sembra molto più complessa. Gli stessi Greci, che per primi la tradussero in una teoria matematica, non furono capci di darle un concetto intuitivo. Oggi tutti sappiamo che due rette sono ortogonali se incontrandosi formano quattro angoli retti, ma nessuno -matematico,fisico,ingegnere,economista o biologo- è in grado di spiegarci in maniera semplice che cosa sia una ngolo retto.
In effetti, in natura la perpendicolarità è una nozione che non compare mai, se non nelle forze centrali, ma anche là sembra essere stata soppiantata da nuove teorie, in cui le forze centrali sono casi particolari di campi di forze che -visti da altri osservatori-in realtà seguono linee curve. Per fare un esempio pratico, lanciamo in aria un pallone sulla nostra testa e facciamolo ricadere. A noi sembra che ricade in direzione perpendicolare al suolo, ma agli occhi di un abitante di Alpha Centauri che ci osserva con il suo ipertelescopio, di perpendicolare non c'è nullla, c'è una piccola sfera che prima si allontana e poi entra in contatto con una superficie curva, la Terra. Probabilmente, l'intuizione più profonda del concetto di perpendicolarità l'ha avuta il matematico Pitagora, che ha caratterizzato due lati perpendicolari con il suo celebre teorema.
La matematica del XXI secolo ha stabilito di racchiudere il concetto di "perpendicolarità" nella teoria degli spazi di Banach. Quanto noi stiamo per fare, quindi, è lo studio di un concetto apparentemente noioso ed elementare, che studiato con strumenti complessi si traforma forse in un "giacimento di petrolio matematico": un campo affascinante e ancora inesplorato.
Nel piano cartesiano, vale il seguente
Teorema 7.1 Due rette sono perpendicolari se il prodotto dei loro coefficienti angolari è uguale a -1
dimostrazione. Sia la famiglia di rette
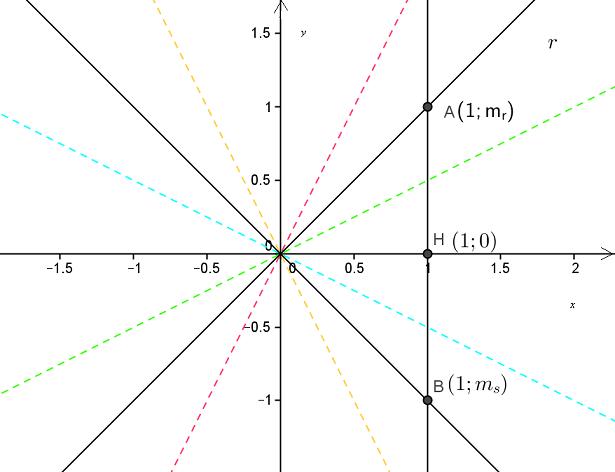
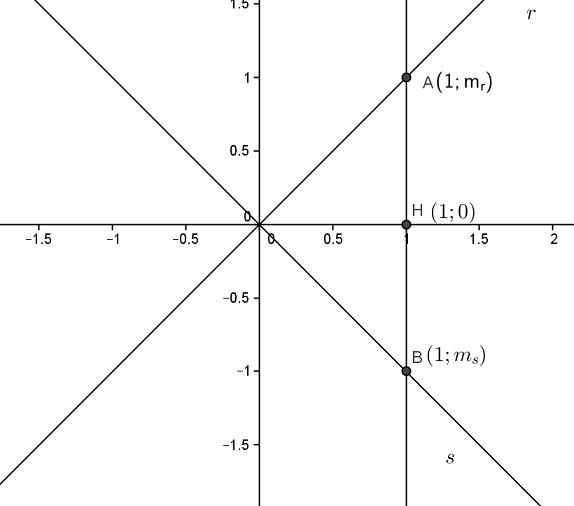
tutte le rette passano per l'origine degli assi e tra queste ce ne sono solo due che sono perpendicolari. Indichiamo queste due rette con r ed s, e quindi le loro equazioni saranno,rispettivamente
![]()
e
Sia la retta di equazione x=1 e siano A e B le intersezioni della retta con r ed s. Di conseguenza,sarà A(1,mr) e B(1;mr). Sia H(1,0) l'intersezione della retta x=1 con l'asse y. Per ipotesi, il triangolo OAB è rettangolo. Per il secondo teorema di euclide, l'altezza OH sarà media proporzionale tra le proiezioni dei due cateti sull'ipotenusa, AH e BH.
Ma
e
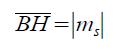
quindi , siccome per il secondo terema di Euclide
![]()
si ha che
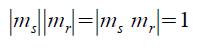
siccome mr e ms sono di segno opposto, deve essere
![]()
(QED)
Vale anche il viceversa
Teorema 7.2 Siano r ed s due rette tali che Il prodotto dei loro coefficienti angolari sia -1. Allora r ed s sono perpendicolari.
Dimostrazione. Siano due rette r ed s di equazione
![]()
e
tali che
![]()
allora
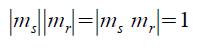
allora, nella figura seguente
e quindi
![]()
siccome OHA e OHB sono due triangoli rettangoli in H
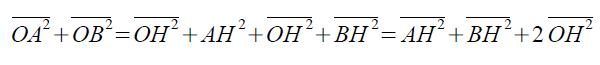
e quindi
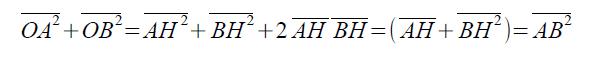
nel triangolo AOB vale il teorema di Pitagora. Di conseguenza, il triangolo AOB è rettangolo in O e quindi le rette r ed s sono perpendicolari. (QED) .
Le dimostrazioni dei due teoremi valgono anche nel caso in cui le due rette non passano per l'origine, perchè la perpendicolarità è invariante per traslazioni. Se spostiamo angoli retti nel piano, gli angoli restano retti.
7.2 Distanza di un punto da una retta
La perpendicolarità è una nozione con cui possiamo rappresentare la distanza di un punto da una retta. Dato un punto e una retta, sembra naturale esprimere la distanza del punto dalla retta come il minimo cammino che li unisce, ovvero la proiezione ortogonale del punto sulla retta.
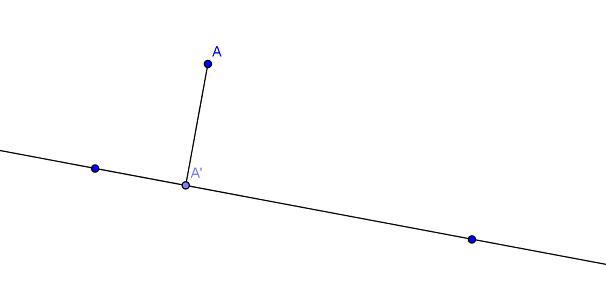
Data l'equazione di una retta r e le coordinate di un punto P, ci proponiamo di trovare una formula per il calcolo della distanza di P da r
Teorema 7.3 Sia P (xP,yP) un punto e r una retta di equazione
Allora la distanza di P da r è data dalla formula
![]()
Il contenuto di questa pagina è interamente sotto la responsabilità dell'autore, Per imprecisioni ed errori, scrivere a ferrante.formato@istruzione.it .
Ultima modifica, 19 luglio 2015, ore 16.19















