 |
|
costo misto |
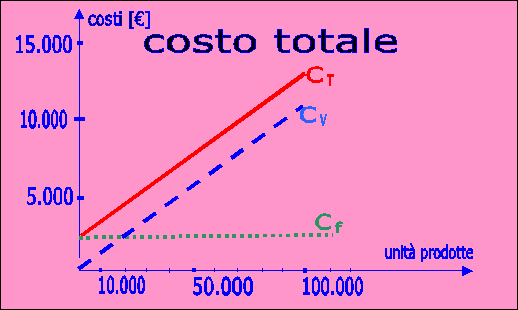
Costo totale e punto di pareggio
Vediamo ora il costo totale per un singolo prodotto. Nella scorsa lezione abbiamo visto sia i costi fissi Cf che i costi variabili Cv per il singolo prodotto. Il costo totale CT sostenuto dall'azienda per l'intero prodotto lo possiamo ottenere facendo la somma dei due costi e cioè:
CT = Cf + Cv
Possiamo anche fare una rappresentazione grafica del costo totale:
 |
|
costo misto |
Il costo totale è un costo misto, cioè è costituito da una parte fissa e da una parte variabile. Ci possiamo ora calcolare il costo unitario totale per ogni unità del singolo prodotto dividendo il costo totale per la quantità prodotta.
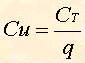
dove Cu è il costo unitario totale, CT è il costo totale, e q è la quantità di prodotto.
E' evidente che all'aumentare della produzione il costo unitario del singolo prodotto diminuisce.
Ritorniamo all'esempio della copiatrice, e considerando che i costi fissi siano di 3.720 € e i costi variabili unitari della singola copia pari 0,0949, possiamo fare la seguente tabella in base alle quantità prodotte:
|
copie prodotte q |
costi fissi Cf |
costo unitario variabile cu |
costo variabile Cv |
costo totale CT |
costo unitario totale Cu |
| 1 | 3.720 | 0,0949 | 0,0949 | 3.720,09 | 3.720,0949 |
| 1.000 | 3.720 | 0.0949 | 94,90 | 3.814,90 | 3,8149 |
| 5.000 | 3.720 | 0.0949 | 474,50 | 4.194,50 | 0,8389 |
| 10.000 | 3.720 | 0,0949 | 949,00 | 4.669,00 | 0,4669 |
| 20.000 | 3.720 | 0,0949 | 1.898,00 | 5.618,00 | 0,2809 |
| 50.000 | 3.720 | 0,0949 | 4.745,00 | 8.465,00 | 0,1693 |
| 84.931 | 3.720 | 0,0949 | 8.059,95 | 11.779,95 | 0,1387 |
| 100.000 | 3.720 | 0,0949 | 9.490,00 | 13.210,00 | 0,1321 |
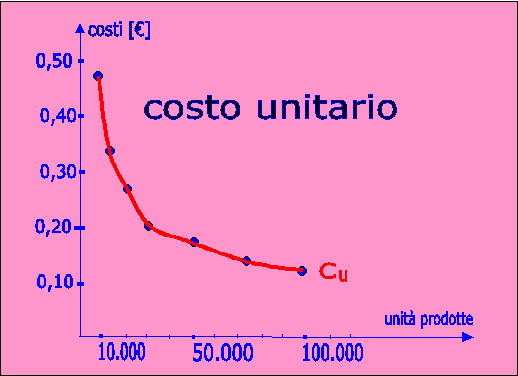
Con i dati del costo unitario totale Cu di questa tabella possiamo rappresentare su un diagramma come varia il costo unitario totale al variare delle quantità:
 |
|
costo unitario totale al variare di q |
Dal diagramma vediamo come il costo unitario diminuisca all'aumentare delle quantità prodotte, per il fatto della minore incidenza dei costi fissi all'aumentare delle quantità.
Esercizio da svolgere
Una azienda ha dei costi fissi pari a 250.000 € per la produzione di un singolo prodotto il cui costo unitario variabile è pari a 50 €. Disegnare un diagramma che indichi l'andamento del costo misto totale e del costo unitario totale al variare della produzione da 0 a 5.000 unità.
I ricavi delle vendite o delle prestazioni
Per ottenere i ricavi delle vendite del prodotto o i corrispettivi delle prestazioni effettuate, possiamo moltiplicare le quantità vendute q per il prezzo di vendita unitario p. In formula abbiamo:
R = q x p
Dove R rappresenta il ricavo IVA esclusa, q le quantità vendute, e p il prezzo di vendita, IVA esclusa.
Nei riguardi dell'IVA occorre fare alcune considerazioni.
L'imposta sul valore aggiunto ( I.V.A. )
L'IVA è l'imposta sul valore aggiunto dall'impresa nella costruzione di un prodotto o nella prestazione di un servizio. Essa è stata istituita dal Decreto del Presidente della Repubblica 26 ottobre 1972, n. 633 - Istituzione e disciplina sul valore aggiunto.
Per calcolare l'IVA si determina dapprima la base imponibile, cioè l'intero costo aziendale del singolo prodotto, maggiorato dell'utile che si vuole conseguire. Nell'esempio delle copie abbiamo visto che il costo della singola copia ammontava a 0,1321 € e su di esso abbiamo ritenuto di applicare un utile del 5% e cioè 0,0066 € ed abbiamo ottenuto un prezzo di vendita:
p = 0,1321 + 0,0066 = 0,1387 €
prezzo da intendersi senza IVA. Questo prezzo è detto imponibile ai fini IVA. Su questo imponibile occorre applicare una percentuale che rappresenta l'IVA da pagare, tale percentuale, che di solito è il 20%, è detta aliquota.
Una formula utilizzata può essere la seguente:
PIVATO = p x 1,20
questa formula deriva dalla seguente:
PIVATO = p + 20% di p
Quando diciamo il venti per cento, in realtà diciamo il 20 su cento, cioè il 20 diviso 100, cioè:
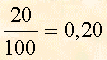
Controlla con la Calcolatrice.
Per cui la formula diventa:
PIVATO = p + 0,20 x p
Mettiamo ora in evidenza o a fattor comune P ed otteniamo:
PIVATO = (1 + 0,20) x p = 1,20 x p
Conoscendo, invece il prezzo IVA compresa, possiamo depurare l'IVA e riottenere il prezzo senza IVA, facendo la formula inversa, cioè:
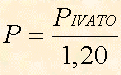
Esempio
Calcoliamo il prezzo IVA compresa, con aliquota del 20%, considerando come imponibile il prezzo di una copia p = 0,1387 €
Soluzione
Applichiamo la formula:
PIVATO = p x 1,20
PIVATO = 0,1387 x 1,20 = 0,16644 €
Controlla con la Calcolatrice.
Esempio
Calcoliamo il prezzo netto, senza IVA, con aliquota del 20%, considerando come prezzo lordo di una copia PIVATO = 0,16644 €.
Soluzione
Con la formula inversa otteniamo:
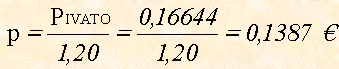
Controlla con la Calcolatrice.
Dai calcoli effettuati risulta che il cliente deve pagare il 20% di IVA calcolato sul prezzo p di vendita voluto dall'azienda. Tale imposta deve essere versata mensilmente a cura dell'impresa all'Erario. Tuttavia, è consentita la detrazione dell'IVA pagata sugli acquisti effettuati dall'azienda stessa. Se nel calcolo dei costi dell'azienda si sono sempre considerati tutti i costi di acquisto al netto di IVA, possiamo ritenere che l'IVA non influenzi il prezzo di vendita p calcolato in precedenza, senza conteggiare l'IVA. Tuttavia questa è solo una approssimazione dei calcoli, in quanto può avvenire che non tutta la produzione aziendale sia venduta al cliente finale; ma, molto spesso, restano dei prodotti invenduti, i quali aumentano i costi di produzione.
Le considerazioni che ora faremo sul punto di pareggio si basano su questa approssimazione e cioè supponiamo che tutta la merce prodotta sia stata venduta, in tale ipotesi i costi calcolati, e calcolati trascurando l'IVA di acquisto, possono ritenersi corrispondenti alla realtà.
Rappresentiamo, ora, l'andamento dei ricavi totali R in funzione delle quantità prodotte sullo stesso diagramma dei costi totali CT, con i valori della seguente tabella:
|
copie prodotte q |
costo totale CT |
prezzo unitario senza IVA p |
ricavo totale senza IVA R |
| 1 | 3.720,09 | 0,1387 | 0,1387 |
| 1.000 | 3.814,90 | 0,1387 | 138,70 |
| 5.000 | 4.194,50 | 0,1387 | 693,50 |
| 10.000 | 4.669,00 | 0,1387 | 1.387,00 |
| 20.000 | 5.618,00 | 0,1387 | 2.774,00 |
| 50.000 | 8.465,00 | 0,1387 | 6935,00 |
| 84.931 | 11.779,95 | 0,1387 | 11.779,92 |
| 100.000 | 13.210,00 | 0,1387 | 13.870,00 |
Nella tabella notiamo un particolare numero di copie, cioè 84.931 copie, nel quale il costo totale equivale al ricavo totale;. Questo rappresenta il punto di pareggio.
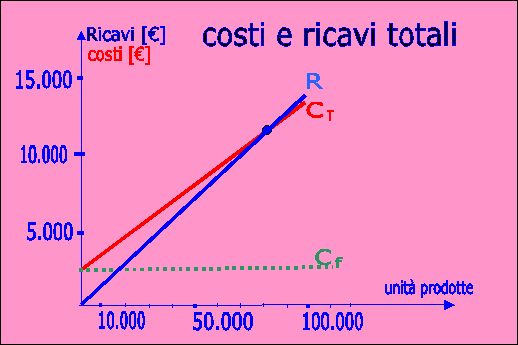 |
| andamento dei costi e ricavi totali |
Nel diagramma il punto di pareggio è quello di intersezione tra la retta dei costi totali e la retta dei ricavi totali. Il punto di pareggio, detto anche break even, rappresenta la perfetta coincidenza tra ricavi e costi totali per il singolo prodotto o per l'intera azienda; nel punto di pareggio vi è un equilibrio economico, cioè il reddito della impresa è nullo, cioè non vi sono perdite e non vi sono utili.
Stiamo attenti che il punto di pareggio è sostenibile dall'azienda per parecchio tempo, in quanto l'azienda è in grado di pagare tutti i costi sostenuti, senza indebitarsi. E tra i costi è compreso anche il lavoro dell'imprenditore nell'azienda. Per vendite inferiori alle quantità previste nel punto di pareggio l'azienda è in perdita, e tale condizione non può essere sostenuta per molto tempo. Per quantità vendute superiori al punto di pareggio, invece, l'azienda ne ricava un utile.
Determinazione matematica del punto di pareggio
Essendo il reddito R:
R = Ricavo totale - Costi totali
il punto di equilibrio è quello in cui il reddito è uguale a zero e cioè quello in cui i ricavi sono uguali ai costi.
Ricordando che i ricavi sono:
R = q x p
mentre i costi totali sono:
CT = Cf + Cv
e i costi totali variabili Cv li possiamo calcolare con la formula:
Cv = q x cu
dove Cv è il costo totale variabile, q è la quantità, cu è il costo unitario variabile.
L'equazione:
CT = Cf + Cv
diventa:
CT = Cf + q x cu
Facendo la differenza
R - CT
e ponendola uguale a zero:
R - CT= 0
otteniamo:
R - CT = q x p - Cf - q x cu = 0
Portiamo Cf al secondo membro:
q x p - q x cu = Cf
mettiamo a fattore comune q
q x ( p - cu ) = Cf
da cui q, cioè la q di pareggio Qp sarà:
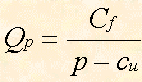
che poi sarebbe:

Nell'esempio della copiatrice, ricordando che il costo unitario variabile era cu = 0,0949 €; che il prezzo unitario senza IVA era p = 0,1387 €, che i costi fissi erano Cf =3.720 €, otteniamo:
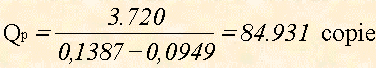
Copie che rappresentano il punto di pareggio.
I due metodi grafico
 |
| andamento dei costi e ricavi totali |
e matematico, ovviamente, danno lo stesso risultato.
Consideriamo, ora, la differenza che compare al denominatore:
( p - cu )
cioè la differenza tra prezzo unitario di vendita e costo variabile unitario; questa differenza è detta margine unitario di contribuzione mu.
La parola margine indica in genere una differenza, nel nostro caso indica la differenza tra i ricavi e i costi variabili relativi al singolo prodotto; la parola contribuzione sta a significare il contributo che il singolo prodotto dà per la copertura dei costi fissi aziendali; unitario sta a significare che è riferito all'unità di prodotto. Questo margine unitario di contribuzione mu non rappresenta per se stesso un utile per l'azienda; ma diventa un utile unitario quando questo margine di contribuzione si riferisce ad un prodotto che ha superato il punto di pareggio.
Vediamo, ora, come cresce il margine di contribuzione totale all'aumentare delle quantità prodotte, nell'esempio della copiatrice.
|
copie prodotte q |
prezzo unitario senza IVA p |
costo unitario variabile cu |
margine unitario di contribuzione mu= p - cu |
Margine totale di
contribuzione
MT = q x mu |
| 1 | 0,1387 | 0,0949 | 0,0438 | 0,0438 |
| 1.000 | 0,1387 | 0,0949 | 0,0438 | 43,80 |
| 5.000 | 0,1387 | 0,0949 | 0,0438 | 219,00 |
| 10.000 | 0,1387 | 0,0949 | 0,0438 | 438,00 |
| 20.000 | 0,1387 | 0,0949 | 0,0438 | 876,00 |
| 50.000 | 0,1387 | 0,0949 | 0,0438 | 2.190,00 |
| 84.931 | 0,1387 | 0,0949 | 0,0438 | 3.719,99 |
| 100.000 | 0,1387 | 0,0949 | 0,0438 | 4.380,00 |
Ricordiamo che proprio 3.720 € erano i costi fissi Cf. Dalla tabella vediamo come nel punto di pareggio il margine di contribuzione totale equivale proprio ai costi fissi; quindi per la quantità di 84.931 copie l'azienda, avendo raggiunto la copertura di tutti i costi fissi, ha raggiunto il punto di pareggio.
Nel diagramma:
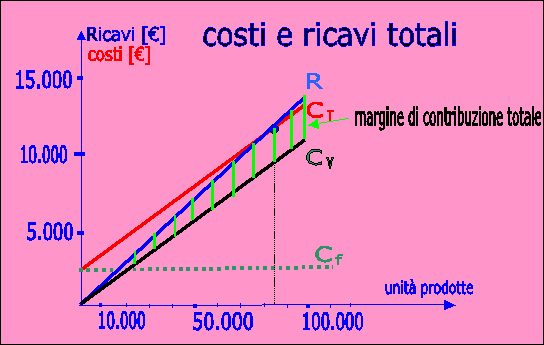 |
| tratteggio verde chiaro per il margine di contribuzione totale |
rappresentiamo con il tratteggio verde chiaro il margine totale di contribuzione MT al variare delle quantità. Se dal grafico scaliamo verticalmente tutti i segmenti che rappresentano i margini di contribuzione totale per le rispettive quantità, o riportiamo i dati dalla tabella, otteniamo l'andamento della retta che esprime il margine totale di contribuzione al variare delle quantità prodotte.
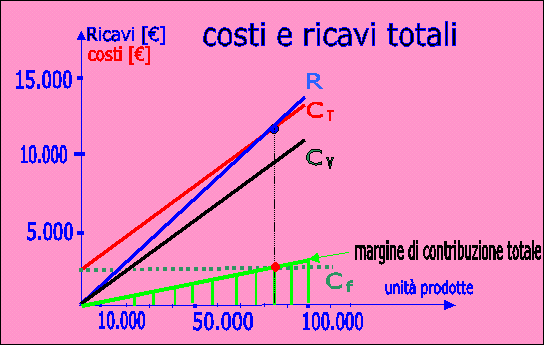 |
| intersezione tra retta del margine di contribuzione e retta dei costi fissi |
La intersezione, della retta che rappresenta l'andamento del margine totale di contribuzione con la retta che rappresenta i costi fissi, ci dà nuovamente il punto di pareggio, inteso come equivalenza tra margine di contribuzione totale e costi fissi.
Le due equazioni viste sopra
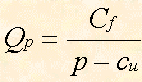
che poi sarebbe:

le possiamo ora interpretare dal punto di vista del margine di contribuzione unitario ( P - cu ), che poi è quello che compare al denominatore, e quindi trasformarle nelle seguenti:
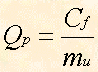
dove Qp è la quantità del punto di pareggio, Cf sono i costi fissi, mu è il margine unitario di contribuzione, cioè:
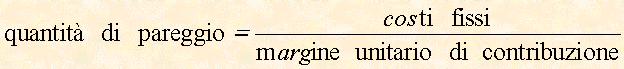
In conclusione il margine unitario di contribuzione indica quanto un singolo prodotto contribuisce, attraverso le vendite, alla copertura dei costi fissi. Quando raggiungiamo il punto di pareggio il margine totale di contribuzione è già in grado di assorbire tutti i costi fissi; superata la quantità del punto di pareggio si ha un utile per l'azienda; mentre al di sotto del punto di pareggio, poiché il margine di contribuzione totale non riesce a coprire tutti i costi fissi, vuol dire che l'azienda si trova in perdita.
Comprendiamo, quindi, l'importanza del punto di pareggio per le scelte dei Direttori sia di funzione, sia di divisione sia generali, per le decisioni strategiche o tattiche che devono prendere.
Lezioni di sistemi organizzativi aziendali