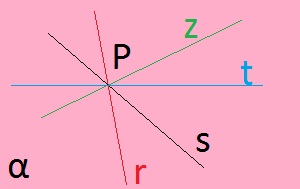
per un punto passano infinite rette
Il piano e la retta
| data di oggi: |
La bella geometria
Il piano geometrico è un insieme infinito di punti. Non possiamo disegnarlo tutto su un foglio di carta o sulla lavagna, ma possiamo disegnare solo una parte. Il piano lo indichiamo con una lettera dell'alfabeto greco; per esempio: α = alfa, β = beta, eccetera.
|
|
|
per un punto passano infinite rette |
Se disegniamo un punto P possiamo disegnare molte rette che passano per quel punto P. Per dire "molte" in geometria si usa una parola più precisa, cioè "infinito". Per cui diciamo che: per un punto P passano infinite rette.
Infinito può essere sia un sostantivo, sia un aggettivo, con maschile singolare= infinito, femminile singolare = infinita, maschile plurale = infiniti e femminile plurale = infinite.
A volte per indicare l'infinito usiamo il simbolo ∞ = infinito, che è un numero molto grande, miliardi di miliardi.
|
|
|
per due punti passa una sola retta |
Se disegniamo due punti A e B su di un piano alfa, notiamo che la retta che possiamo disegnare è una sola; per cui diciamo: per due punti passa una sola retta.
Il tratto di retta compreso tra i punti A e B è detto segmento AB. Il segmento AB è compreso nella retta r.
|
|
|
due semirette |
Se di una retta consideriamo un punto qualsiasi, per esempio il punto O, possiamo dire che esso divide la retta in due parti uguali, una parte si trova a destra del punto, l'altra parte si trova a sinistra del punto. Ognuna delle due parti è detta semiretta.
|
|
|
segmento AB e segmento CD |
Se invece consideriamo due punti diversi di una retta, il tratto di retta compreso tra i due punti è detto segmento. Nella figura di sopra abbiamo due segmenti: il segmento AB e il segmento CD. Il punto da cui inizia un segmento si dice estremo del segmento; anche il punto con cui finisce un segmento di dice estremo del segmento.
Il segmento è solamente lungo, infatti la retta ha solo la lunghezza, cioè è sottile e non è né larga né alta. La lunghezza del segmento coincide con la distanza tra i due punti estremi del segmento.
|
|
|
due segmenti consecutivi |
Due segmenti si dicono consecutivi se hanno un solo estremo in comune e non si trovano sulla stessa retta.
|
|
|
due segmenti adiacenti |
Due segmenti si dicono adiacenti se hanno un solo estremo in comune e si trovano sulla stessa retta.
Confronto di segmenti
Il confronto tra due segmenti è importante in quanto noi riusciamo a conoscere la misura di un altro segmento senza doverlo misurare. Questo succede molto spesso, specie per chi viaggia in aereo o in automobile. Se infatti si vuole conoscere la distanza tra due auto o tra due velivoli che viaggiano a velocità elevate, risulta impossibile prendere un metro e misurare la loro distanza, distanza che occorre conoscere in ogni istante per evitare che i velivoli o le auto collidano tra di loro, o come si dice volgarmente, avvenga un incidente.
|
|
|
aereo in volo |
I segmenti si misurano in metri, cioè l'uomo ha preso un segmento campione, cioè ha preso un pezzo fatto del metallo platino in lega con l'iridio, ha disegnato su questo pezzo un segmento, cioè ha segnato due punti ed ha deciso che la distanza tra questi due punti valga un metro. Questo metro campione si trova a Parigi, in Francia. Poi qualcuno ha stabilito che la luce e le onde radio viaggiano da un punto all'altro alla velocità di 300.000 km/s, cioè trecentomila chilometri al secondo, sempre facendo riferimento a questo metro campione. Per cui se vogliamo conoscere la distanza, istante per istante, tra due auto o tra due aerei basta misurare il tempo che percorre un'onda elettromagnetica inviata con un radar sul velivolo in movimento, per risalire alla distanza tra due punti con la formula:
d = 150.000 T
dove d è la distanza, misurata i chilometri, tra due punti e T è il tempo, misurato in secondi, che un'onda radio percorre partendo dal punto in cui noi ci troviamo, cioè dal radar o dal nostro smartphone munito di GPS che abbiamo in mano, colpendo il bersaglio di cui vogliamo conoscere la distanza e ritornando al punto di partenza.
|
|
|
grandi antenne che inviano onde radio nello spazio |
In commercio esistono diversi mezzi per misurare la lunghezza; si può usare il metro detto del falegname;
|
|
|
metro del falegname |
è un metro pieghevole, costituito da segmenti lunghi 20 cm. Oppure si può usare il metro a nastro che usa un ingegnere.
|
|
|
metro a nastro dell'ingegnere |
Quando disegniamo un segmento su carta o sul computer, possiamo usare un righello.
|
|
|
righello di carta o di plastica |
Il righello è una piccola riga, su cui sono disegnati i centimetri e i millimetri. Poiché di solito noi disegniamo su carta, usiamo i sottomultipli del metro, cioè dividiamo il metro in 100 parti o in mille parti. I sotto multipli del metro sono:
| si scrive | si legge | si divide il metro | si ottiene |
| dm | decimetro | per 10 | 0,1 m |
| cm | centimetro | per 100 | 0,01 m |
| mm | millimetro | per 1000 | 0,001 m |
Se, invece, dobbiamo misurare oggetti molto lunghi usiamo i multipli del metro, cioè moltiplichiamo il metro per 100 o per mille. I multipli del metro sono:
| si scrive | si legge | si moltiplica il metro | si ottiene |
| dam | decametro | per 10 | 10 m |
| hm | ettometro | per 100 | 100 m |
| km | chilometro | per 1000 | 1000 m |
Per disegnare un segmento lungo 5 cm su un foglio di carta:
|
|
|
segmento lungo 5 cm |
prendiamo un righello ed una matita, partiamo dallo zero ed arriviamo fino al numero 5.
|
|
|
segmenti congruenti lunghi 5 cm |
Se due segmenti hanno la stessa lunghezza si dicono congruenti. La parola congruente sta a significare che hanno la stessa lunghezza. Nel disegno di sopra vediamo il segmento AB che è lungo 5 cm; vediamo il segmento CD che è lungo 5 cm. Avendo la stessa lunghezza possiamo dire che il segmento AB è congruente al segmento CD.
|
|
|
segmento AB maggiore di CD |
Se la lunghezza del segmento AB è maggiore della lunghezza del segmento CD si dice che i segmenti non sono uguali, non sono congruenti ed in particolare AB è maggiore di CD. La parola "maggiore" si abbrevia con il simbolo ">" che si legge "maggiore". Quindi:
AB > CD
si legge:"AB maggiore di CD".
|
|
|
segmento AB minore di CD |
Se la lunghezza del segmento AB è minore della lunghezza del segmento CD si dice che i segmenti non sono uguali, non sono congruenti ed in particolare AB è minore di CD. La parola "minore" si abbrevia con il simbolo "<" che si legge "minore". Quindi:
AB < CD
si legge:"AB minore di CD".
prof. Pietro De Paolis
Corso di geometria per scuola media
Corso di matematica per scuola media
|
|
Indice di tutte le pagine del sito