Le frazioni
| data di oggi: |
Matematica utile
Oggi parliamo delle frazioni.
La frazione è una divisione tra uno o più numeri.
Esempio
![]()
E' una frazione; essa indica che il numero che si trova sopra va diviso con il numero che si trova sotto.
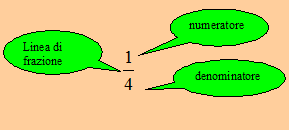
Cioè dobbiamo fare:
1:4
Dividendo 1:4 otteniamo:
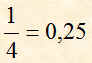
Il numero che otteniamo dalla divisione, cioè il quoziente, di solito è un numero decimale.
Gli elementi del simbolo della frazione sono:
1) - Una linea orizzontale per separare i due numeri; la linea orizzontale è detta linea di frazione.
2) - un primo numero posto sopra la linea di frazione; questo numero è detto numeratore.
3) - Un secondo numero posto sotto la linea di frazione; questo numero è detto denominatore.
Operazioni con le frazioni
Essendo le frazioni dei numeri decimali possiamo eseguire le quattro operazioni anche sulle frazioni.
Addizione
Per sommare due frazioni tra di loro, basta dividere il numeratore di ogni frazione per il suo denominatore e fare la somma delle due somme ottenute.
Esempio
Sommare le due frazioni seguenti:
![]()
Svolgimento
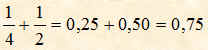
Esistono delle frazioni che hanno lo stesso denominatore; per esempio le due frazioni seguenti:
![]()
In tal caso sommando le due frazioni si ottiene una terza frazione che ha lo stesso denominatore; e come numeratore ha la somma dei due numeratori; cioè:
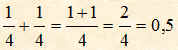
Se le frazioni hanno il denominatori diversi non si possono sommare tra di loro con la regola precedente, ma occorre dividere prima i numeratori con i denominatori di ciascuna e poi fare la somma delle due somme.
Per sommare un numero con una frazione occorre dividere il numeratore della frazione per il suo denominatore e poi fare la somma dei due numeri.
Esempio
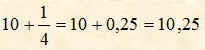
Sottrazione
Per sottrarre due frazioni tra di loro, basta dividere il numeratore di ogni frazione per il suo denominatore e fare la differenza delle due somme ottenute.
Esempio
Sottrarre le due frazioni seguenti:
![]()
Svolgimento
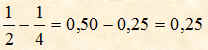
Esistono delle frazioni che hanno lo stesso denominatore; per esempio le due frazioni seguenti:
![]()
In tal caso facendo la differenza tra le due frazioni si ottiene una terza frazione che ha lo stesso denominatore; e come numeratore ha la differenza dei due numeratori; cioè:
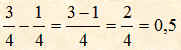
Se le frazioni hanno il denominatori diversi non si può fare la sottrazione con la regola precedente, ma occorre dividere prima i numeratori con i denominatori di ciascuna e poi fare la differenza delle due somme.
Per sottrarre una frazione da un numero occorre dividere il numeratore della frazione per il suo denominatore e poi fare la differenza dei due numeri.
Esempio
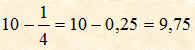
Moltiplicazione
Per moltiplicare due frazioni tra di loro, basta dividere il numeratore di ogni frazione per il suo denominatore e fare il prodotto delle due somme ottenute.
Esempio
Moltiplicare le due frazioni seguenti:
![]()
Svolgimento
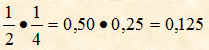
Un altro modo per eseguire la moltiplicazione tra due frazioni è quello di moltiplicare dapprima tutti i numeratori tra di loro e mettere il prodotto ottenuto come numeratore di un'altra frazione; successivamente si moltiplicano tutti i denominatori tra di loro e si mette il prodotto ottenuto come denominatore della frazione ottenuta come prodotto delle due frazioni. per esempio le due frazioni seguenti:
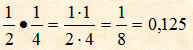
Per moltiplicare un numero per una frazione basta moltiplicare il solo numeratore per i numero dato; mentre il denominatore resta uguale, senza moltiplicarlo.
Esempio
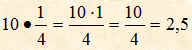
Divisione
Per dividere due frazioni tra di loro, basta dividere il numeratore di ogni frazione per il suo denominatore e fare la divisione delle due somme ottenute.
Esempio
Dividere le due frazioni seguenti:
![]()
Svolgimento

Un altro modo per eseguire la divisione tra due frazioni è quello di moltiplicare il numeratore della prima frazione per il denominatore della seconda frazione e mettere il prodotto ottenuto come numeratore di un'altra frazione; successivamente si moltiplica il denominatore della prima frazione per il numeratore della seconda frazione e si mette il prodotto ottenuto come denominatore della frazione ottenuta come quoziente delle due frazioni. Per esempio le due frazioni seguenti:
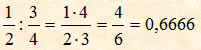
Per dividere un numero per una frazione basta moltiplicare il numero per il denominatore della frazione e mettere il prodotto ottenuto come numeratore della frazione risultante; mentre il numeratore della frazione passa a denominatore della frazione risultante.
Esempio
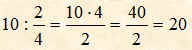
Potenza di una frazione
La potenza di una frazione si ottiene moltiplicando la frazione per se stessa tante volte quanto indicato dall'esponente della potenza.
Esempio
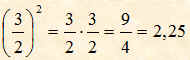
Nei calcoli può esser utile la seguente tabellina delle moltiplicazioni.
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
prof. Pietro De Paolis
Corso di matematica per scuola media
|
|
Indice di tutte le pagine del sito