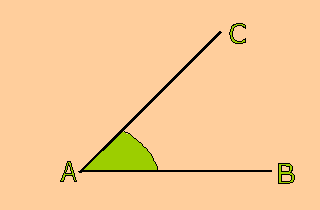
angolo
Il poligono parte 2 su 2
| data di oggi: |
La bella geometria
Vediamo ora gli angoli nei poligoni.
Si chiama angolo di un poligono una parte di piano compresa tra due lati di un poligono.
|
|
|
angolo |
Due lati consecutivi formano due angoli, cioè un angolo interno al poligono ed un angolo esterno al poligono. La somma dell'angolo interno più tutto l'angolo esterno è pari a 360 gradi, cioè i due angoli sono supplementari.
|
|
Tuttavia mentre l'angolo interno si considera tutto, per l'angolo esterno si considera solo una parte, quella necessaria a raggiungere nella somma i 180 gradi. In tal modo la somma dell'angolo interno più l'angolo esterno è pari a 180°, quindi i due angoli sono supplementari.
L'angolo esterno si chiama anche angolo adiacente l'angolo interno, in quanto la loro somma è pari a 180°. Un angolo di 180° è detto angolo piatto.
Somma degli angoli interni
Per calcolare la somma di tutti gli angoli interni di un poligono, si contano il numero dei lati; dal numero dei lati si sottrae il numero 2; il risultato si moltiplica per 180°.
La formula è la seguente:
Si = (n-2) · 180°
dove Si è la somma degli angoli interni;
n è il numero di lati.
Quindi la somma degli angoli interni di un poligono è pari al numero di lati meno due, moltiplicato per 180°.
Dimostrazione
Consideriamo dapprima un triangolo qualunque, cioè un triangolo scaleno, con i lati tutti di diversa lunghezza.
|
|
Indichiamo con la lettera greca
a ( alfa ) l'angolo interno nel vertice A; indichiamo con la lettera b ( beta ) l'angolo interno nel vertice B; indichiamo con la lettera g (gamma) l'angolo interno nel vertice C.Partendo dal vertice B tiriamo una parallela al lato AC, indichiamo con r questa retta parallela. Essa forma un angolo a con la retta passante per il lato AB, essendo appunto parallela ad AC.
Se consideriamo le due rette parallele una passante per AC e l'altra retta r che parte dal vertice B, e consideriamo la trasversale BC, cioè un segmento che interseca le due rette parallele, esse formano angoli alterni interni congruenti, cioè della stessa misura.
Nel nostro caso ci interessa l'angolo g colorato in verde.
Ne consegue che:
a+b+g= 180°
Quindi la somma degli angoli interni di un triangolo è pari a 180°. Non solo, ma ogni angolo esterno ad un triangolo è pari alla somma degli altri due angoli interni.
La formula:
Si = (n-2) · 180° = (3-2)· 180° = 180°
è vera per il triangolo.
Cioè la somma degli angoli interni di un triangolo è sempre 180°.
Per dimostrare la formula negli altri poligoni procediamo in questo modo.
|
|
Dividiamo il poligono in un certo numero di triangoli, disegnando le diagonali interne, cioè le rette che uniscono due vertici diversi.
Nel quadrilatero otteniamo due triangoli. Poiché la somma degli angoli interni di un triangolo è 180°, la somma degli angoli interni di due triangoli è 360°.
Quindi la formula è vera anche per il quadrilatero:
Si = (4-2) · 180° = (2)· 180° = 360°
Nel pentagono otteniamo tre triangoli. Poiché la somma degli angoli interni di un triangolo è 180°, la somma degli angoli interni di tre triangoli è 540°.
Quindi la formula è vera anche per il pentagono:
Si = (5-2) · 180° = (3)· 180° = 540°
Nell'esagono otteniamo quattro triangoli. Poiché la somma degli angoli interni di un triangolo è 180°, la somma degli angoli interni di quattro triangoli è 720°.
Quindi la formula è vera anche per l'esagono:
Si = (6-2) · 180° = (4)· 180° = 720°
prof. Pietro De Paolis
Corso di geometria per scuola media
Corso di matematica per scuola media
|
|
Indice di tutte le pagine del sito