|
|
|
Zitto! |
Parla! |
La piramide
| data di oggi: |
La bella geometria
Consideriamo la piramide.
|
|
|
piramide |
La piramide è una figura geometrica che appartiene allo spazio; infatti ha una lunghezza, ha una larghezza, ha un'altezza. Se consideriamo la superficie esterna notiamo che essa è costituita da un rettangolo di base.
Al posto del rettangolo si può usare anche il quadrato. Oppure come base vi è un qualunque altro poligono regolare.
Il poligono che sta sotto è detto base.
Vi è, quindi, una sola base, cioè la base inferiore.
L'altezza della piramide è proprio la distanza tra la base e il vertice della piramide.
Superficie della piramide
Per calcolare la superficie della piramide occorre tenere conto sia della base che della superficie laterale.
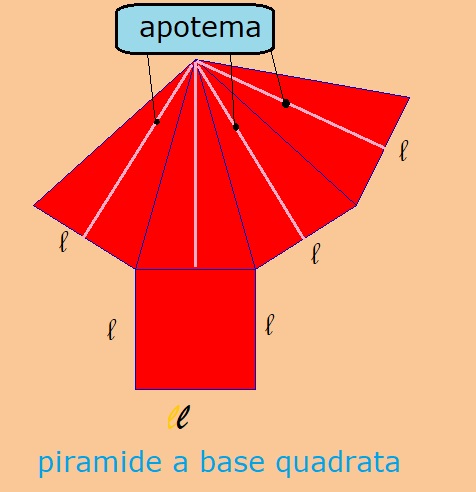
La superficie laterale è tutta la superficie eccetto la base. Essendo la base un quadrato o un poligono, ci possiamo calcolare il perimetro della base con la formula:
p = 4 l
dove l è la misura del lato del quadrato.
Se la base della piramide è un rettangolo:
|
|
|
rettangolo |
il perimetro è la somma dei quattro lati del rettangolo.
Se la base è un pentagono:
|
|
|
pentagono |
il perimetro è la somma dei cinque lati del pentagono. Analogamente per gli altri poligoni usati come base della piramide.
La superficie laterale è la somma di tanti triangoli isosceli quanti sono i lati. Se i lati sono quattro, come nella base quadrata, vi sono quattro triangoli isosceli, aventi tutti la stessa area, in quanto la base di ogni triangolo è uguale al lato del quadrato.
L'altezza di ciascuno dei quattro triangoli si chiama apotema della piramide.
L'apotema della piramide è sempre maggiore dell'altezza della piramide e della metà del lato di base della piramide; infatti l'apotema della piramide è l'ipotenusa di un triangolo rettangolo.
Per cui l'area della superficie laterale, che indichiamo con Al , la possiamo calcolare con la formula:
Al =
Al
=
Notiamo che, essendo la base costituita da un quadrato, possiamo calcolare l'area del quadrato di base la formula:
B = lato2
Mentre la superficie totale, che indichiamo con At, è data dalla formula
At =
+ l2
cioè dobbiamo sommare alla superficie laterale la superficie della base.
Esempio
Una piramide ha il lato di base di base l = 6 cm; mentre l'apotema a = 5 cm.
Calcolare la superficie totale di tutta la piramide.
Svolgimento
Occorre calcolare la superficie della base con la formula:
B = l2
Sostituiamo i valori ed otteniamo:
B = l2 = 6 x 6 = 36 cm2
La base ha la superficie di :
B = 36 cm2
Ci calcoliamo ora la superficie laterale con la formula:
AL
=
Sostituiamo i valori ed otteniamo:
Al
=
= 60
Di conseguenza la superficie totale della piramide è:
At = Al + B = 60 + 36 = 96 cm2
La superficie totale della piramide misura 96 cm2
Volume della piramide
Il volume della piramide è la parte di spazio occupata dalla stessa piramide. Il volume lo indichiamo con la lettera V maiuscola. Per calcolare il volume si usa la seguente formula:
V =
dove B indica la superficie della base inferiore ed h indica l'altezza della piramide.
Il volume ha come unità di misura il m3 o il cm3, cioè metro cubo o centimetro cubo.
Esempio
Una piramide a base quadrata ha il lato di base l = 6 cm; mentre l'altezza h = 4 cm.
Calcolare il volume della piramide.
Svolgimento
Ricordando la formula:
V =
andiamo a calcolarci prima B, cioè la superficie della base, che è un quadrato; otteniamo:
B = l2 = 6 x 6 = 36 cm2
Poi sostituiamo i valori ed otteniamo:
V =
=
= 48 cm3
Il volume della piramide misura 48 cm3
*******************
Formule da ricordare
|
piramide |
|
| Al =
At =
|
Al = superficie laterale in
m2 o cm2 At = superficie totale in m2 o cm2 a = apotema in m o cm l= lato della base in m o cm |
V =
|
V = volume della piramide in
m3 o cm3 B = superficie della base in m2 o cm2 h = altezza della piramide in m o cm |
| h =
|
|
| B =
|
|
prof.
Corso di matematica per scuola media
|
|
Indice di tutte le pagine del sito