parallelepipedo
Il parallelepipedo rettangolo
| data di oggi: |
La bella geometria
Consideriamo il parallelepipedo.
|
|
|
parallelepipedo |
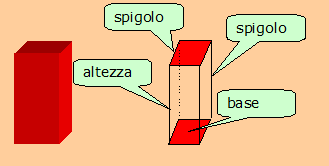
Il parallelepido è una figura geometrica che appartiene allo spazio; infatti ha una lunghezza, ha una larghezza, ha un'altezza. Se consideriamo la superficie esterna notiamo che essa è costituita da molti rettangoli messi insieme; precisamente i rettangoli sono sei.
Il rettangolo che sta sotto tutti gli altri è detto base.
Il rettangolo che sta sopra tutti gli altri è detto base.
Vi sono, quindi, due basi; la base inferiore e la base superiore. Le due basi sono dei rettangoli che hanno la stessa superficie e gli stessi lati.
Ogni lato di un rettangolo è detto spigolo.
Vi sono 4 spigoli verticali. Ogni spigolo verticale è detto altezza del parallellepido. Tutti gli spigoli verticali hanno la stessa lunghezza.
Vi sono 8 spigoli orizzontali; 4 spigoli per la base inferiore e 4 spigoli per la base superiore.
Un caso particolare di parallelepipedo è quello in cui tutti e 12 gli spigoli sono uguali come lunghezza.
|
|
|
cubo |
Una figura solida che ha tutti gli spigoli uguali si dice cubo. Nel cubo tutte le facce sono costituite da quadrati. Vi sono esattamente 6 facce. L'altezza del cubo è uguale ai lati di uno qualunque dei quadrati che costituiscono le 6 facce.
Superficie del parallelepipedo rettangolo
Per calcolare la superficie del parallelepipedo occorre tenere conto che esso ha sei facce. Ogni faccia è costituita da un rettangolo. Per calcolare tutta la superficie esterna occorre quindi sommare la superficie di tutte e sei le facce. Cioè calcolare le superfici di 6 rettangoli e sommarle tra di loro.
Notiamo che essendo le due basi costituite da rettangoli eguali le due basi hanno la stessa superficie.
Anche le facce verticali sono costituite da rettangoli tutti eguali, cioè che hanno i lati a due a due eguali. per cui basta calcolare la superficie di un rettangolo laterale e moltiplicarla per 4.
Esempio
Un parallelepipedo rettangolo ha come base un rettangolo i cui lati sono:
2 lati da 2 cm
2 lati da 4 cm
Inoltre i rettangoli che costituiscono le facce laterali hanno l'altezza di 10 cm.
Calcolare la superficie di tutto il parallelepipedo.
Svolgimento
Occorre calcolare le superfici di 6 rettangoli e sommarle tra di loro.
Cominciamo dalle sue basi.
Indichiamo con S1 la superficie della base inferiore. Essa è uguale a:
S1 = b1 x h1 = 4 x 2 = 8 cm2
Indichiamo con S2 la superficie del rettangolo superiore. Essa è uguale a:
S2 = b2 x h2 = 4 x 2 = 8 cm2
Indichiamo con S3 la superficie di una faccia laterale. Essa è uguale a:
S3 = b3 x h3 = 4 x 10 = 40 cm2
Indichiamo con S4 la superficie di una faccia laterale. Essa è uguale a:
S4 = b4 x h4 = 4 x 10 = 40 cm2
Indichiamo con S5 la superficie di una faccia laterale. Essa è uguale a:
S5 = b5 x h5 = 2 x 10 = 20 cm2
Indichiamo con S6 la superficie di una faccia laterale. Essa è uguale a:
S6 = b6 x h6 = 2 x 10 = 20 cm2
La superficie totale ST del parallelepipedo rettangolo sarà data dalla somma delle superfici delle 6 facce.
ST = S1+ S2+ S3+ S4+ S5+ S6 = 8 + 8 + 40 + 40 +20 +20 = 136 cm2
La superficie del parallelepipedo misura 136 cm2
Volume del parallelepipedo rettangolo
Il volume del parallelepipedo è la parte di spazio occupata dallo stesso parallelepipedo. Il volume lo indichiamo con la lettera V maiuscola. Per calcolare il volume si usa la seguente formula:
V = S x h
dove S indica la superficie della base inferiore ed h indica l'altezza del parallelepipedo, cioè indica la lunghezza di uno dei 4 spigoli verticali.
Il volume ha come unità di misura il m3 o il cm3, cioè metrocubo o centimetrocubo.
Esempio
Un parallelepipedo rettangolo ha come base un rettangolo i cui lati sono:
2 lati da 2 cm
2 lati da 4 cm
Inoltre i rettangoli che costituiscono le facce laterali hanno l'altezza di 10 cm.
Calcolare il volume del parallelepipedo rettangolo.
Svolgimento
Ricordando la formula:
V = S x h
andiamo a calcolarci prima S, cioè la superficie del rettangolo di base; otteniamo:
S = b x h = 2 x 4 = 8 cm2
Poi sostituiamo i valori ed otteniamo:
V = S x h = 8 x 10 = 80 cm3
Il volume del parallelepipedo misura 80 cm3
*******************
Formule da ricordare
|
parallelepipedo rettangolo |
|
| ST = S1+ S2+ S3+ S4+ S5+ S6 | S = superficie in
m2 o cm2
h = altezza in m o cm |
V = S x h |
S = superficie della base in
m2 o cm2
h = altezza in m o cm |
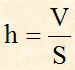
|
|
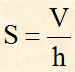
|
|
prof. Pietro De Paolis
Corso di matematica per scuola media
|
|
Indice di tutte le pagine del sito