La dinamica
| data di oggi: |
La dinamica del moto circolare uniforme
La dinamica studia i corpi in movimento.
Alcune equazioni della dinamica le abbiamo già considerate.
Abbiamo visto che il moto si chiama moto circolare quando il percorso segue la circonferenza di un cerchio.
Abbiamo visto che:
v = ω r
Questa formula ci dice che la velocità tangenziale v è il prodotto della velocità angolare ω per il raggio r.

Abbiamo visto che l'accelerazione centripeta ac è:
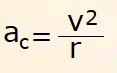
Questa formula ci dice che l'accelerazione centripeta ac in modulo è uguale al rapporto tra la velocità al quadrato rispetto al raggio r.
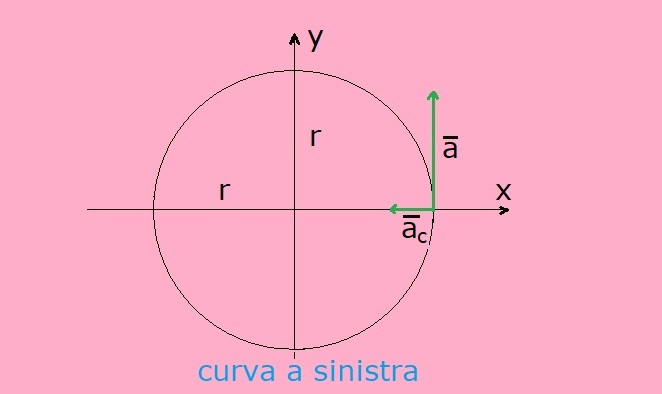
Il verso del vettore accelerazione ac è verso il centro della circonferenza; la direzione è quella del raggio.
Consideriamo ora il principio fondamentale della dinamica, cioè il Principio di azione delle forze o principio di Galileo, la cui formula è:
F = m a
Questa formula ci dice che il vettore forza è direttamente proporzionale al vettore accelerazione che indichiamo con a
Al posto di a mettiamo il valore
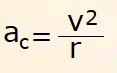
in quanto nel moto circolare uniforme l'accelerazione tangenziale è nulla, essendo la velocità costante. Otteniamo:
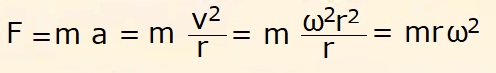
cioè:
F
= m r ω2Dove F è la forza centripeta, diretta verso il centro della circonferenza, m la massa del corpo, r il raggio della circonferenza ed ω la sua velocità angolare.
Questa formula ci dice che nel moto circolare uniforme la forza centripeta è direttamente proporzionale alla massa del corpo che ruota, alla sua distanza dal centro e al quadrato della sua velocità angolare.
E' un corso a pagamento dal costo di 3 € per 365 giorni.
![]()
Tecnologia per la scuola media
Indice di tutte le pagine del sito