|
|
|
|
|
|
|
|
Sistema di numerazione binario
Si dice sistema binario un sistema di numerazione che si basa su due soli simboli o cifre, che sono: 0 (zero) e 1. Dal punto di vista circuitale lo 0 può essere realizzato portando il punto di un circuito elettrico ad un livello di tensione basso come nel seguente schema:
|
|
|
|
|
|
|
|
Punto A collegato a massa ( zero logico )
Essendo il punto A collegato a massa, esso ha una tensione pari a: 0 V, cioè tensione nulla; quindi esso rappresenta lo zero dal punto di vista della logica elettronica.
La cifra
1, invece, può essere realizzata portando il punto del circuito ad un livello di tensione alto, come nel seguente schema: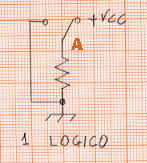
Punto A collegato a + Vcc ( uno logico )
Essendo il punto A collegato alla tensione di alimentazione +Vcc, esso ha un elevato valore di tensione, e quindi mi rappresenta la cifra 1 nella logica elettronica.
Realizzazione in laboratorio
Volendo realizzare in laboratorio i circuiti di sopra possiamo utilizzare una normale basetta per i collegamenti.

basetta dei collegamenti
La basetta dei collegamenti serve per montare i circuiti elettrici in un modo veloce, con collegamenti mobili. Essa è composta da alcuni fori praticati in un supporto di materiale isolante. I fori sono collegati tra di loro nella parte interna non visibile.
Alcuni fori sono collegati in modo orizzontale ed altri in modo verticale, secondo il seguente schema:

Collegamenti della basetta dei collegamenti
Sul lato sinistro della basetta dei collegamenti si dispone della tensione di alimentazione; nel nostro caso abbiamo una tensione continua.
 |
|
|
Fotografia del circuito |
schema elettrico |
Resistore collegato a massa, quindi zero logico
Volendo invece realizzare il livello logico 1 colleghiamo i componenti nel seguente modo:
 |
|
| fotografia del circuito | schema elettrico |
Resistore collegato alla tensione di alimentazione, cioè 1 logico
Il sistema binario è un sistema
posizionale, in quanto le due cifre assumono un valore diverso, secondo la posizione in cui si trovano, secondo il seguente schema:|
1 |
1 |
1 |
1 |
1 |
|
24 |
23 |
22 |
21 |
20 |
|
16 |
8 |
4 |
2 |
1 |
Questo vuol dire che se la cifra 1 si trova nella prima posizione, a partire da destra verso sinistra, vale 1; nella seconda vale 2; nella terza vale 4; nella quarta vale 8; nella quinta vale 16; e così continuando secondo le potenze del 2. Se invece la cifra è 0 vale sempre 0, però non si può omettere perché serve per la posizione delle cifre. Esempio il numero binario 1011 vale 8 + 0 + 2 + 1 = 11.
Sui numeri binari è possibile fare le operazioni algebriche di somma, sottrazione, moltiplicazione e divisione. Riportiamo solo le regola della somma:
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 1 con riporto di 1
SISTEMA DI NUMERAZIONE ESADECIMALE
Un sistema di numerazione si dice
esadecimale se si basa su sedici cifre. Le cifre usate sono 0,1,2,3,4,5,6,7,8,9,10,A,B,C,D,E,F che si trovano in corrispondenza con i numeri binari e decimali, come nella seguente tabella:|
ESADECIMALE |
BINARIO |
DECIMALE |
|
0 |
0000 |
0 |
|
1 |
0001 |
1 |
|
2 |
0010 |
2 |
|
3 |
0011 |
3 |
|
4 |
0100 |
4 |
|
5 |
0101 |
5 |
|
6 |
0110 |
6 |
|
7 |
0111 |
7 |
|
8 |
1000 |
8 |
|
9 |
1001 |
9 |
|
A |
1010 |
10 |
|
B |
1011 |
11 |
|
C |
1100 |
12 |
|
D |
1101 |
13 |
|
E |
1110 |
14 |
|
F |
1111 |
15 |
Il sistema esadecimale ha il vantaggio di poter raggruppare un numero binario avente diverse cifre in un numero esadecimale con minori cifre. Esempio
F racchiude 1111.
Indice di tutte le pagine del sito