Calcolatore geometrico
Il calcolatore geometrico è una applicazione
che consente di scrivere la traccia di un problema di geometria presa da un
libro di testo di scuola media; se la traccia del problema è scritta in modo
corretto ed appartiene ai circa 500.000 problemi inseriti nella applicazione, la
soluzione del problema viene subito visualizzata.
Non esistono più le versioni gratuite di questa
applicazione.
La versione a pagamento aggiornata si trova
alla pagina:
Calcolatore geometrico
La nostra applicazione risiede sui server sicuri, in modo che
la password non venga intercettata e letta dagli hacker.
Lingue straniere
Per le lingue di inglese, spagnolo e francese
vi sono diverse versioni gratuite, ma non aggiornate. Vi sono anche delle
applicazioni per smartphone gratuite; l'elenco completo si trova alla pagina:
Indice del sito Scuola Elettrica
Maggiori informazioni
Le informazioni per i prodotti gratuiti si
trovano alla pagina:
Informazioni sul
risolutore di problemi gratuito
Vediamo, ora come funziona il calcolatore
geometrico aggiornato. Il primo modulo è costituito dal correttore e analizzatore.
Questo modulo analizza le frasi e le parole scritte nell'enunciato del problema;
ogni dato numerico viene memorizzato insieme alle unità di misura.
Esempio
L'area della superficie laterale di una piramide regolare
quadrangolare è 13/5 dell'area di base e la loro differenza è di 640 cm².
Calcola l'area totale e il volume della piramide.
La frase:
L'area della superficie laterale di una piramide regolare
quadrangolare è 13/5 dell'area di base
viene analizzata
dal punto di vista numerico; il numero 13/5 viene inteso come una frazione e
memorizzato in una variabile.
La frase:
e la loro differenza è di 640 cm²
viene analizzata
dal punto di vista numerico; il numero 640 viene inteso come un valore numerico;
mentre cm² viene memorizzato
come unità di misura di superficie e area.
La frase:
Calcola l'area totale e il volume della piramide.
viene analizzata come richiesta del problema.
E' importante specificare cosa si vuole, cioè se si vuole solo l'altezza della
piramide, o solo il volume. Nel nostro caso si chiede area totale e volume;
ovviamente, poiché per calcolare il volume occorre conoscere prima l'altezza del
solido, l'applicazione calcola sia l'altezza e sia l'apotema, necessario per
calcolare l'altezza.
Le parole chiave e i dati numerici vengono
passati al secondo modulo, che è quello che cerca una soluzione al problema
proposto.
Il secondo modulo analizza i dati forniti in
ingresso e le richieste del problema. Le richieste sono obbligatorie, non si può
scrivere genericamente: Piramide ?
Al limite si può scrivere:
differenza = 640
rapporto laterale = 13/5
altezza della piramide quadrangolare?
Cioè occorre specificare che si tratta di una
piramide e di una piramide quadrangolare, cioè con base un quadrato.
La soluzione data è la seguente:
Svolgimento del problema
Dati
La differenza di area laterale - area di base = 640 cm²
area laterale = 13/5 x area di base
Soluzione

Essendo area laterale 13/5 volte area di base posso considerare che le parti
della differenza sono:
13 - 5 = 8 parti
Ora divido la differenza in 8 parti e ottengo
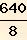 = 80 cm²
= 80 cm²
Quindi area di base = 5 x 80 = 400 cm²
area laterale = 13 x 80 = 1040 cm²
Risposta
area laterale = 1040 cm²
area di base = 400 cm²
Se conosco le equazioni posso usare un secondo metodo di risoluzione.
Dati
La differenza di area laterale - area di base = 640 cm²
area laterale = 13/5 x area di base
Soluzione
Mi calcolo una equazione sapendo che
area laterale = 13/5 x area di base
e che
la differenza di area laterale - area di base = 13/5 x area di base - area di
base = 640 cm²
da cui
area di base =
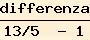 =
=
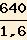 = 400 cm²
= 400 cm²
area laterale = 13/5 x area di base = 13/5 x 400 = 1040 cm²
Risposta
area di base = 400 cm²
area laterale = 1040 cm²
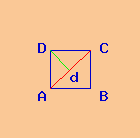
Dati
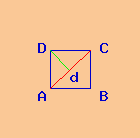
Poligono: quadrato ABCD
area A = 400 cm²
Soluzione
Si richiede il lato l del quadrato ABCD avente area A = 400 cm².
Applico la formula:
l = V A
ed ottengo:
l = V 400 = 20 cm
Risposta
Il lato del quadrato ABCD è 20 cm
Dati
Poligono: quadrato ABCD
lato l = AB = 20 cm
Soluzione
Si richiede il perimetro del quadrato ABCD i cui lati sono:
AB = BC = CD = DA = 20 cm
Applico la formula:
p = AB + BC + CD + DA
ed ottengo:
p = 20 cm + 20 cm + 20 cm + 20 cm = 80 cm
Risposta
Il perimetro del quadrato ABCD è 80 cm
Dati
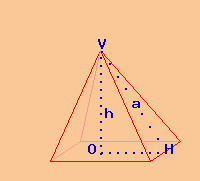
Solido: piramide quadrangolare
area laterale Al = 1040 cm²
perimetro di base p = 80 cm
Soluzione
Si richiede l'apotema a di una piramide
quadrangolare la cui area laterale Al = 1040 cm²
e il cui perimetro di base p = 80 cm
Applico la formula:
a =
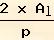 ed ottengo:
ed ottengo:
a =
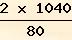 = 26 cm
= 26 cm
Risposta
L'apotema a della piramide quadrangolare è 26 cm
Calcolo metà lato di base sapendo che:
lato = 20 cm
rapporto = 2
Applico la formula:
metà lato di base =
 ed ottengo:
ed ottengo:
metà lato di base =
 = 10 cm
= 10 cm
Risposta
metà lato di base è 10 cm
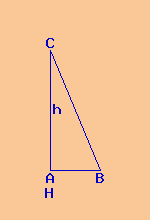
Dati:
Poligono: triangolo rettangolo ABC
cateto c = AB = 10 cm
ipotenusa a = BC = 26 cm
Soluzione
Si richiede un cateto di un triangolo rettangolo ABC avente:
cateto c = AB = metà lato = 10 cm
ipotenusa a = BC = apotema = 26
cm
Applico la formula derivata dal teorema di Pitagora:
cateto b = CA = altezza piramide
= V a² - c² ed ottengo:
cateto b = V(26 cm)² - (10 cm)² =
24 cm
Risposta
L'altro cateto b = CA del
triangolo rettangolo ABC, che coincide con altezza piramide, è 24 cm.
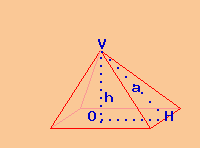
Dati
Solido: piramide quadrangolare
area di base B = 400 cm²
altezza h = 24 cm
Soluzione
Si richiede il volume di una piramide quadrangolare la cui area della superficie
di base è:
B = 400 cm²
la cui altezza h = 24 cm
Applico la formula:
V =
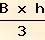 ed ottengo:
ed ottengo:
V =
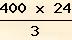 = 3200 cm³
= 3200 cm³
Risposta
Il volume della piramide quadrangolare è 3200 cm³
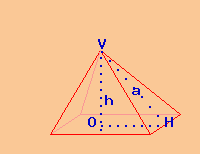
Dati
Solido: piramide quadrangolare
perimetro di base p = 80 cm
area di base B = 400 cm²
apotema a = 26 cm
Soluzione
Si richiede l'area della superficie totale di una piramide quadrangolare
regolare il cui perimetro di base è:
p = 80 cm
la cui area della superficie di base è B = 400 cm2
il cui apotema è a = 26 cm
Applico la formula:
At =
 + B ed ottengo:
+ B ed ottengo:
At =
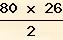 +
400 cm² = 1440 cm²
+
400 cm² = 1440 cm²
Risposta
L'area della superficie totale della piramide quadrangolare è 1440 cm².
Tempo impiegato per risolvere il problema: 0 secondi
Se nei dati vi sono due diverse unità di
misura, cioè alcune in cm ed altre in metri, i dati vengono riportati tutti alla
prima unità di misura inserita, facendo le opportune equivalenze tra unità di
misura. Il disegno delle varie figure geometriche viene
riportato in scala in base alle dimensioni assegnate. Notare i vari passaggi del
problema; tra le varie soluzioni viene scelta la più semplice, cioè quella
adatta alla scuola media e veloce. In alcuni casi viene aggiunta anche la
soluzione mediante una equazione di primo grado.
Per alcune figure piane, triangolo, quadrato,
rettangolo, parallelogramma, trapezio, è possibile fornire le coordinate
cartesiane dei vertici e chiedere cosa si vuole calcolare.
Esempio
In un sistema cartesiano ortogonale sono
dati i punti A(0;-5), B(9;7), C(-9;7). Che figura ottieni? Trova area e
perimetro.
Il calcolatore geometrico risponde in questo
modo:
Svolgimento del problema
Figura geometrica = triangolo
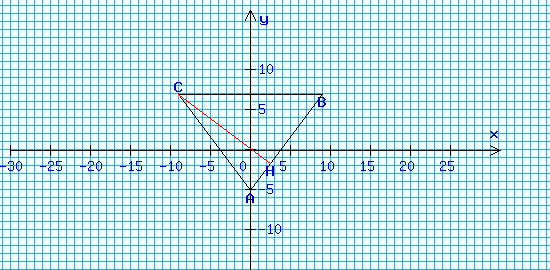
Dati:
Poligono: triangolo ABC
vertice A ( +0 ; -5 )
vertice B ( 9 ; 7 )
vertice C ( -9 ; 7 )
Soluzione
Si richiedono i tre lati e l'altezza di un triangolo ABC avente:
vertice A ( +0 ; -5 )
vertice B ( 9 ; 7 )
vertice C ( -9 ; 7 )
Per il lato AB applico la formula:
AB = V ( xB - xA )² + ( yB - yA )²
ed ottengo:
AB = V ( 9 - ( +0 ) )² + ( 7 - ( -5 ) )²
= 15 m
Per il lato BC applico la formula:
BC = V ( xC - xB )² + ( yC - yB )²
ed ottengo:
BC = V ( -9 - ( 9 ) )² + ( 7 - ( 7 ) )²
= 18 m
Per il lato CA applico la formula:
CA = V ( xA - xC )² + ( yA - yC )²
ed ottengo:
CA = V ( +0 - ( -9 ) )² + ( -5 - ( 7 )
)² = 15 m
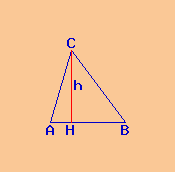
Dati:
Poligono: triangolo isoscele ABC
lato A B = 15 m
lato B C = 18 m
lato C A = 15 m
Soluzione
Si richiede il tipo del triangolo ABC.
Il triangolo è isoscele in quanto ha due lati uguali.
Risposta
Il triangolo è isoscele.
Mi calcolo l'area di un triangolo ABC i cui lati sono:
AB = 15 m
BC = 18 m
CA = 15 m
Mi calcolo il semiperimetro con la formula:
p / 2 = (AB + BC + CA ) / 2
ed ottengo:
p/2 = (15 m + 18 m + 15 m) / 2 = 24 m
Applico la formula di Erone:
A = V p/2 (p/2 - a)(p/2 - b)(p/2-c)
ed ottengo:
A = V 24 (24 - 15)(24 - 18)(24 - 15)
= 108 m2
Mi calcolo l'altezza AH relativa al lato AB.
Applico la formula:
AH =
 ed ottengo:
ed ottengo:
AH =
 = 14,4 m
= 14,4 m
Risposta
Il triangolo isoscele ABC ha:
lato AB = 15 m
lato BC = 18 m
lato CA = 15 m
altezza AH = 14,4 m
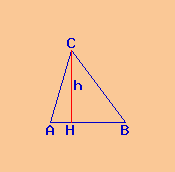
Dati:
Poligono: triangolo ABC
AB = 15 m
BC = 18 m
CA = 15 m
Soluzione
Si richiede il perimetro del triangolo ABC i cui lati sono:
AB = 15 m
BC = 18 m
CA = 15 m
Applico la formula:
p = AB + BC + CA
ed ottengo:
p = 15 m + 18 m + 15 m = 48 m
Risposta
Il perimetro del triangolo ABC è 48 m.
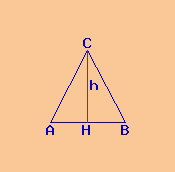
Dati:
Poligono: triangolo ABC
base b = AB = 15 m
altezza h = CH = 14,4 m
Soluzione
Calcolo l'area del triangolo ABC avente:
base b = AB = 15 m
altezza h = CH = 14,4 m
applico la formula A =
&n2=2) ed ottengo:
ed ottengo:
A =
&n2=2) = 108 m²
= 108 m²
Risposta
L'area del triangolo ABC è 108 m²
Tempo impiegato per risolvere il problema: 0 secondi
Errori comuni
Quando si scrive una traccia vi sono molti
errori di trascrizione; alcuni errori vengono corretti in modo automatico, altri
errori di scrittura non vengono corretti.
Questa applicazione non è completa; per
completarla ci vogliono 10 anni, forse 20 anni di lavoro. In questi 20 anni le
tracce proposte cambiano, la lingua scritta e parlata cambia; il significato
dato alle parole cambia. E' difficile ottenere una applicazione perfetta.
A volte occorre usare dei trucchi per ottenere
una risposta esatta; cioè è bene riscrivere la traccia periodo per periodo, con
soggetto predicato e complemento.
A volte occorre chiedere di più di quello che
serve.
Per esempio:
Invece di:
calcola l'altezza.
per alcuni problemi si può scrivere:
calcola il volume.
Oppure
Calcola l'area totale.
In quanto l'applicazione calcola tutti i valori
intermedi necessari per calcolare il volume del solido e l'area totale; quindi
l'altezza viene comunque calcolata.
Quanti problemi risolve?
E' difficile rispondere a questa domanda in
quanto non ho tempo per testare i circa 500.000 problemi che l'applicazione è in
grado di risolvere; sono riuscito a testare circa 4.000 problemi.
Nel giugno 2017 ho inserito due moduli che
combinano tra loro due poligoni alla volta e due solidi alla volta.
Il modulo di due poligoni con dati presi dal
primo e usati per il secondo, e viceversa, dovrebbe da solo risolvere circa
30.000 problemi; ma in realtà sono molti di più.
Il modulo dei solidi, che combina i dati di un
solido con i dati di un altro solido è molto potente; dovrebbe risolvere più di
440.000 problemi diversi, con due solidi.
Poiché vi è un altro modulo che combina dieci o
venti poligoni tra di loro in sequenza e dieci o venti solidi in sequenza tra di
loro, di cui è difficile valutare il numero, posso dire che questa applicazione
può risolvere in automatico più di 500.000 problemi.
Purtroppo non li posso testare tutti.
Versioni in lingua straniera
E' disponibile anche la versione inglese,
spagnola, francese e tedesca.
 |
|
funzionamento risolutore di problemi in inglese |
Come si vede dallo schema la versione inglese
del risolutore di problemi si avvale del risolutore dei problemi in italiano.
Giusto per smentire quanti, per interessi personali, hanno diffuso voci che la
lingua inglese sia necessaria per l'uso del computer. La intelligenza
artificiale, basata sul linguaggio umano, si sviluppa meglio con le lingue
neolatine, quali italiano, spagnolo e francese; questo è dovuto al fatto che la
grammatica latina, e quindi anche quella italiana, che ne rappresenta la
naturale evoluzione, si avvale di articoli, forme verbali, pronomi, sostantivi e
aggettivi che descrivono con precisione una idea espressa in forma scritta;
cosa, questa, che la rozza lingua inglese non permette.
Il programma di risoluzione dei problemi può
dare risposte del tutto errate.
Guida per la risoluzione di problemi di
geometria
Altri esempi di problemi
risolti
prof. Pietro De Paolis
Se ritiene che vi siano altri
errori nel programma di correzione
ci chieda dei chiarimenti:
Richiesta
chiarimenti
