Gli insiemi parte 1
| data di oggi: |
Matematica utile
Oggi parliamo degli insiemi.
In matematica l'insieme è un modo per indicare tante cose o persone che hanno una caratteristica in comune. Coloro che fanno parte di questo insieme si dicono elementi.

Quando si indica un insieme occorre indicare con chiarezza le caratteristiche e le proprietà dell'insieme. In geografia sappiamo che esiste l'Italia, cioè la nazione in cui viviamo. L'Italia è divisa in Regioni; per esempio il Lazio è una regione; la Lombardia è una regione; la Puglia è una regione.
Ogni regione è divisa in province; la provincia è l'insieme di tutti i comuni, cioè di tutte le città che costituiscono la provincia. Per esempio, Roma è sia una città sia una provincia.
Una regione è l'insieme di tutte le province che godono della proprietà di appartenere a quella regione.
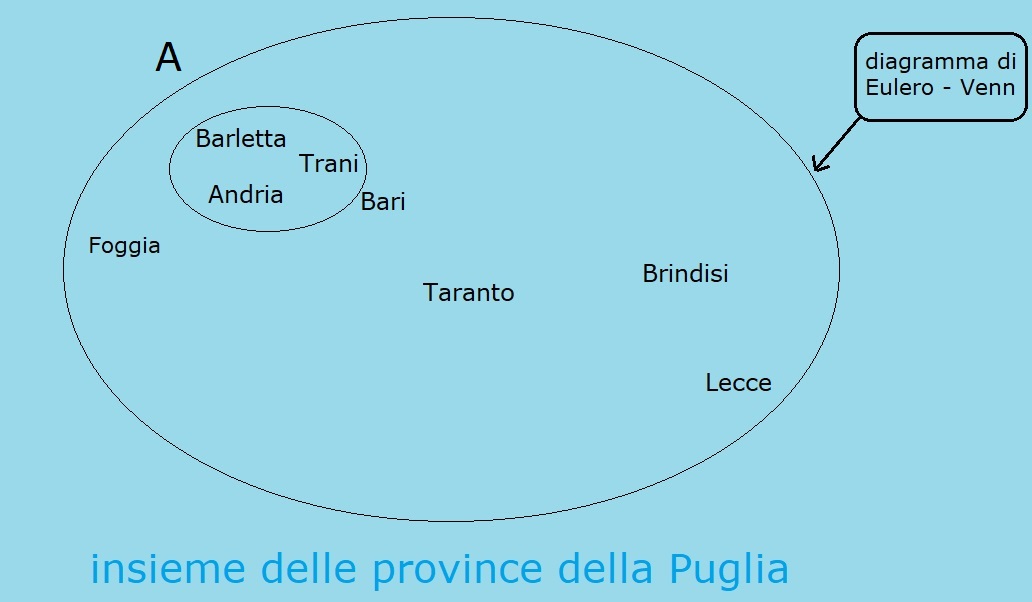
Nell'esempio della Puglia gli elementi dell'insieme Puglia sono le provincie. Bari è una provincia della Puglia; quindi Bari è un elemento dell'insieme Puglia.
Taranto è una provincia della Puglia; quindi Taranto è un elemento dell'insieme Puglia.
Per disegnare un insieme si disegna un grande cerchio e all'interno si mettono tutti gli elementi dell'insieme; tutti, nessuno escluso.

Il grande cerchio che contiene tutti gli elementi dell'insieme si dice diagramma di Eulero; alcuni lo chiamano diagramma di Venn; noi lo chiamiamo diagramma dell'insieme.
Il diagramma è una specie di disegno, fatto su carta o sul tablet o sullo smartphone.
Un altro modo per indicare un insieme è assegnare all'insieme una lettera dell'alfabeto scritta in stampatello maiuscolo.
L'inseme A
L'insieme B
L'insieme C
Gli elementi dell'insieme li possiamo indicare con le lettere minuscuole: a, b, c, d.
Un generico elemento dell'insieme lo possiamo indicare con la lettera x oppure con la lettera y, ma sempre minuscole.
Il minuscolo indica un generico elemento.
Se scrivo:
A = {x │ x è una provincia della regione Puglia}
ho scritto la stessa cosa indicata nel disegno dell'insieme:

La parentesi graffa aperta { indica l'inizio della descrizione dell'insieme A. La parentesi graffa chiusa } indica la fine della descrizione dell'insieme A.
La lettera x indica un generico elemento dell'insieme. La barra dritta verticale │ indica che gode di una proprietà, cioè che possiede una caratteristica.
│ = ha la proprietà di .... oppure ha la proprietà che ...
Riepilogando, se scrivo:
A = {x │ x è una provincia della regione Puglia}
lo leggo in questo modo:
L'insieme A è l'insieme degli elementi x che hanno la proprietà di essere una provincia della regione Puglia.
Oppure scrivo sempre:
A = {x │ x è una provincia della regione Puglia}
ma leggo:
L'insieme A è composto da x che gode della proprietà che x è una provincia della regione Puglia.
Il simbolo
![]() si legge: elemento di..., appartiene a....
si legge: elemento di..., appartiene a....
Se scrivo:
x
![]() A
A
leggo: x appartiene all'insieme A; oppure x è un elemento di A.
Il simbolo
![]() si legge: non elemento di..., non appartiene a....
si legge: non elemento di..., non appartiene a....
Se scrivo:
x
![]() A
A
leggo: x non appartiene all'insieme A; oppure x non è un elemento di A.
Un altro modo per indicare un insieme è quello di mettere il nome di tutti gli elementi dell'insieme.
A = {Foggia, Andria-Barletta-Trani, Bari, Taranto, Brindisi, Lecce}
Questo lo possiamo fare quando gli elementi sono pochi.
Quando un insieme ha molti elementi, cioè migliaia di migliaia, si dice che ha un numero di elementi infinito. In realtà infinito è un numero grandissimo che non si raggiunge mai. Il simbolo dell'infinito è questo:∞, cioè una specie di 8 in posizione orizzontale.
Quando conosciamo con esattezza il numero di elementi di un insieme, l'insieme si dice finito; finito vuol dire che sappiamo il numero di elementi. Per esempio l'insieme delle province della Puglia è costituito da 6 elementi, cioè 6 province, né una di più, né una di meno. Le province della Lombardia sono 12.
1) Bergamo.
2) Brescia.
3) Como.
4) Cremona.
5) Lecco.
6) Lodi.
7) Mantova.
8) Milano.
9) Monza.
10) Pavia.
11) Sondrio.
12) Varese.
Quindi l'insieme:
B = { Bergamo, Brescia, Como, Cremona, Lecco, Lodi, Mantova, Milano, Monza, Pavia, Sondrio, Varese }
è finito, cioè ha un numero esatto di 12 elementi.
A volte un insieme può essere vuoto, cioè non ci sono elementi.
Per esempio l'insieme delle persone aventi una età di 200 anni è vuoto, in quanto nessuno per ora è vissuto per 200 anni. L'insieme vuoto lo indichiamo con il simbolo Ø
Uguaglianza degli insiemi
L'insieme A è uguale all'insieme B se ogni elemento di A è anche elemento di B. Vale il viceversa, cioè ogni elemento di B è anche elemento di A. Cioè i due insiemi hanno gli stessi elementi. Ognuno dei due insieme ha lo stesso numero di elementi.
Esempio
A = {x │ x è una lettera della parola: cane}
B = {x │ x è una lettera della parola: cena}
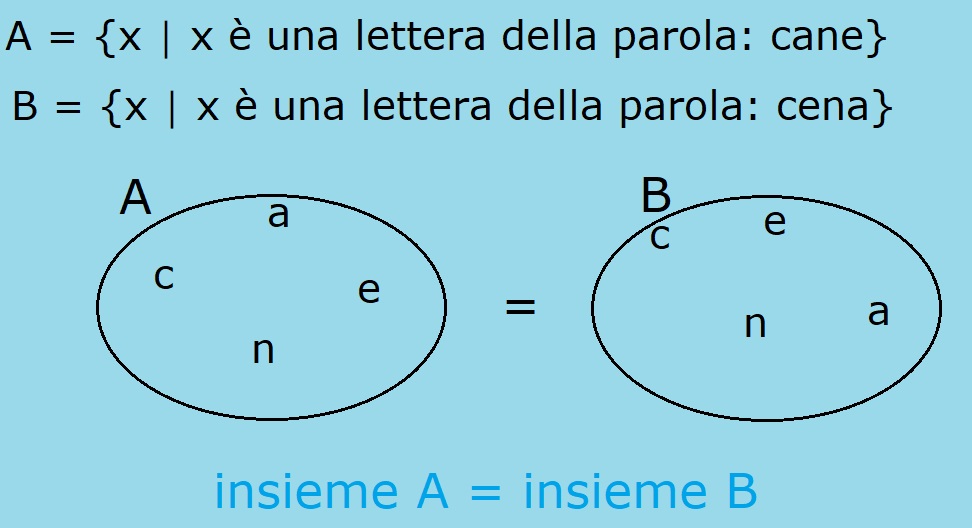
Le due parole: cane e cena, hanno le stesse lettere dell'alfabeto, ma poste in posizione diversa. L'insieme delle lettere della parola cane è uguale all'insieme delle lettere della parola cena. Quindi i due insiemi sono uguali, in quanto hanno gli stessi elementi.
Se, invece, i due insiemi non sono uguali vuol dire che sono diversi l'uno dall'altro; in questo caso usiamo il simbolo ≠, che vuol dire diverso.
Esempio
A = {x │ x è una lettera della parola: cane}
B = {x │ x è una lettera della parola: canile}
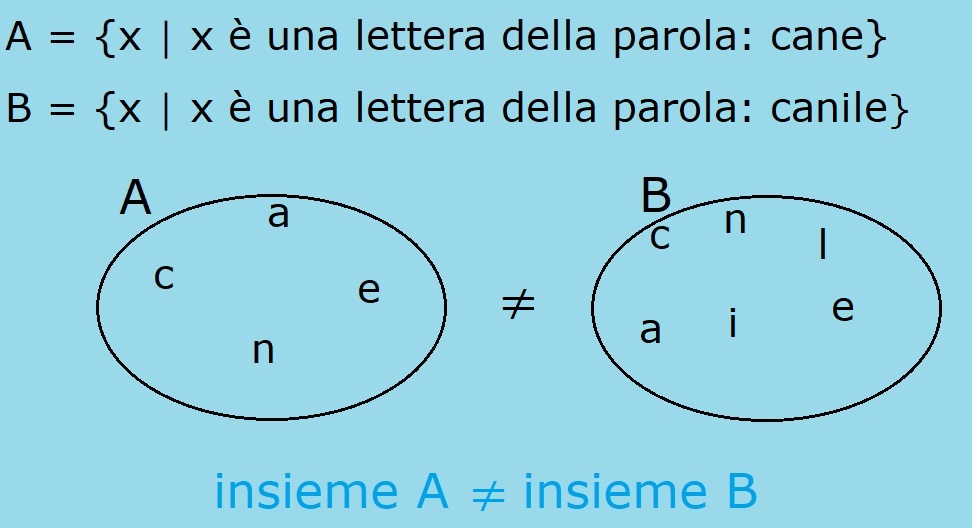
Le due parole: cane e canile, hanno alcune lettere che sono uguali, cioè le lettere della parola cane; ma l'insieme B ha anche le lettere i ed l, che non appartengono ad A, ma appartengono solo a B. Quindi scriviamo:
A ≠ B
in quanto alcuni elementi di B non appartengono ad A.
Sottoinsiemi
Il sottoinsieme è una parte dell'insieme; il sottoinsieme è contenuto nell'insieme principale.
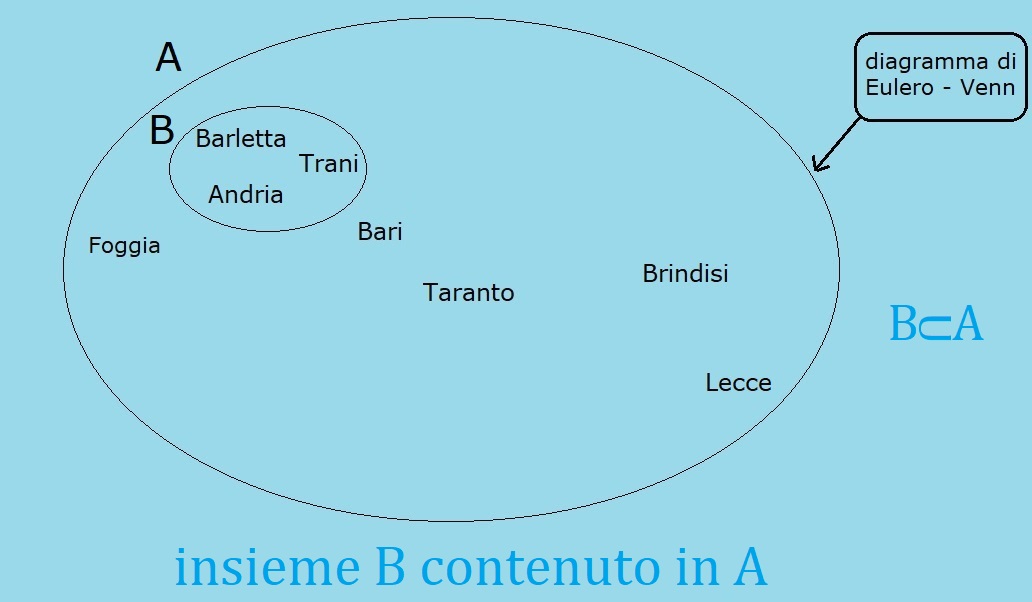
Se consideriamo le province della Puglia notiamo che vi è una provincia costituita da tre città: Barletta, Andria, Trani.
Indichiamo con B le tre città, cioè:
B = {Barletta, Andria, Trani}
Esse costituiscono una solo provincia.
Indichiamo con A l'insieme delle province della Puglia:
A = {Foggia, Andria-Barletta-Trani, Bari, Taranto, Brindisi, Lecce}
oppure
A = {x │ x è una provincia della regione Puglia}
Notiamo che B è contenuto in A, cioè B è una parte di A, cioè B è un sottoinsieme di A.
In simboli scriviamo:
B
![]() A
A
leggiamo: B contenuto in A.
B è un sottoinsieme di A.
Quando un insieme non è contenuto in A scriviamo:
B
![]() A
A
e leggiamo: B non è contenuto in A, cioè B non è un sottoinsieme di A.
Esempio
Consideriamo l'insieme:
A = {x │ x è una lettera della parola: canile}
descrivendo l'insieme A con tutti gli elementi, ho:
A = {c,a,n,i,l,e}
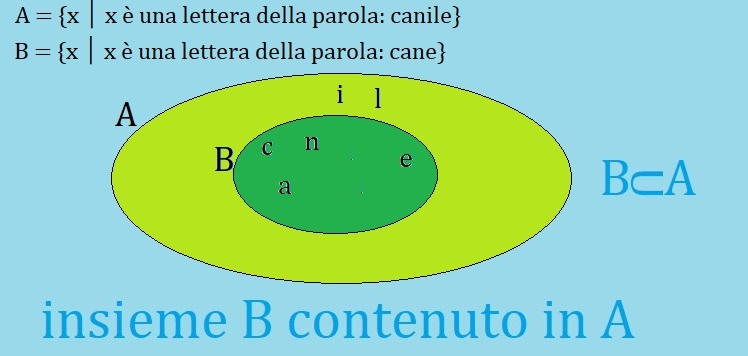
Questa volta A è il canile, mentre B è il cane; il canile è un luogo dove trovano rifugio molti cani.
B = {x │ x è una lettera della parola: cane}
descrivendo l'insieme B con tutti gli elementi, ho:
B = {c,a,n,e}
Le due parole: cane e canile, hanno alcune lettere che sono uguali, cioè le lettere della parola cane; ma l'insieme A ha anche le lettere i ed l, che appartengono solo ad A, ma non appartengono anche B. Quindi scriviamo:
B
![]() A
A
leggiamo: B contenuto in A.
B è un sottoinsieme di A.
Sottoinsieme proprio ed improprio
Purtroppo i matematici sono molto sottili, cioè le hanno studiate tutte per confondere le idee agli altri. Infatti, quando Berta filava, cioè quando anche i matematici e i fisici erano persone semplici, gli insiemi non esistevano in matematica.
Consideriamo il seguente disegno.
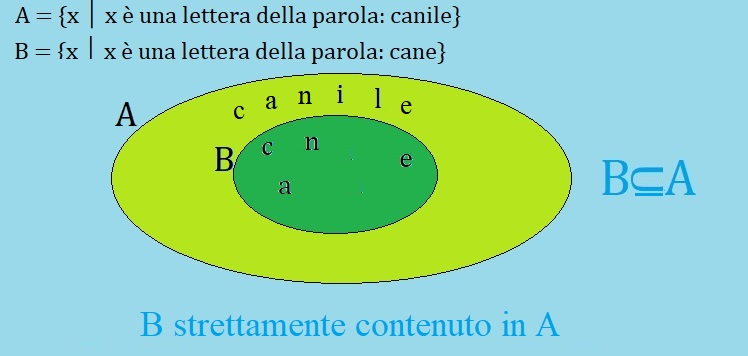
Il disegno sembra uguale a quello di prima, ma non è così. Questa volta l'insieme A contiene sia l'insieme B sia l'insieme A stesso.
A = {{c,a,n,i,l,e}, {c,a,n,e}}
B in questo caso è un sottoinsieme improprio; un sottoinsieme si dice improprio se contiene se stesso oppure contiene l'insieme vuoto.
Quindi scriviamo:
B
![]() A
A
leggiamo: B strettamente contenuto in A.
B è un sottoinsieme improprio di A.
Riepiloghiamo i simboli:
![]() vuol dire: strettamente contenuto in
vuol dire: strettamente contenuto in
L'avverbio: strettamente vuol dire: grosso modo, in modo impreciso, a prima vista.
L'insieme vuoto Ø, quello senza elementi, si può considerare contenuto in tutti gli insiemi.
A = {Ø, {i,l}, {c,a,n,e}}
voglio dire che A contiene sia l'insieme vuoto, sia il sottoinsieme {i,l}, sia il sottoinsieme B={c,a,n,e}
Poiché A contiene l'insieme vuoto, tutti i sottoinsiemi di A sono sottoinsiemi impropri.
Quindi:
Ø
![]() A
A
leggiamo: insieme vuoto è strettamente contenuto in A.
l'insieme vuoto Ø è un sottoinsieme improprio di A.
{i,l}
![]() A
A
leggiamo: insieme costituito da i e da elle è strettamente contenuto in A.
{i,l} è un sottoinsieme improprio di A.
B
![]() A
A
leggiamo: B strettamente contenuto in A.
B è un sottoinsieme improprio di A.
Se, invece, non mettiamo in A né l'insieme vuoto, né l'insieme A stesso, tutti sottoinsiemi di A si dicono insiemi propri di A.
Quindi se scrivo:
A = {{i,l}, {c,a,n,e}}
ho escluso, all'interno di A, sia l'insieme vuoto, sia l'insieme A stesso; posso, quindi, dire:
{i,l}
![]() A
A
leggiamo: insieme i ed elle contenuto in A.
{i,l} è un sottoinsieme proprio di A.
B
![]() A
A
leggiamo: B contenuto in A.
B è un sottoinsieme proprio di A.
prof. Pietro De Paolis
Corso di matematica per scuola media
|
|
Indice di tutte le pagine del sito