Gli insiemi parte 2
| data di oggi: |
Insieme delle parti
Oggi parliamo dell'insieme delle parti di un insieme.
I giorni della settimana sono 7 e sono: lunedý, martedý, mercoledý, giovedý, venerdý, sabato e domenica.
Consideriamo l'insieme dei primi 3 giorni della settimana. Sia
A = {lunedý, martedý, mercoledý}
I sottoinsiemi di A si formano facendo le combinazioni di tutti gli elementi di A.
I sottoinsiemi propri di A sono:
{lunedý}; {martedý};{mercoledý}; {lunedý,martedý}; {lunedý, mercoledý}; {martedý, mercoledý}.
I sottoinsiemi impropri di A sono:
ě; {lunedý, martedý, mercoledý};
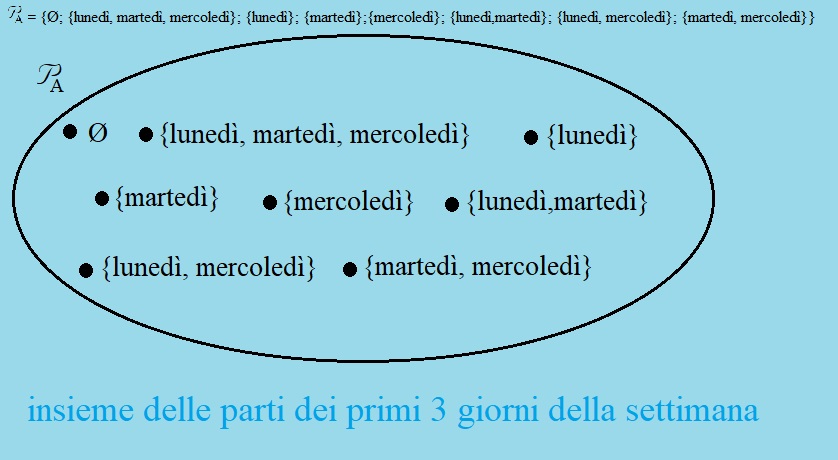
Se consideriamo un altro insieme formato da tutti i sottoinsieme di A, sia sottoinsiemi propri, sia sottoinsiemi impropri, otteniamo un nuovo insieme che si chiama insieme delle parti di A e si indica con il simbolo PA
Il simbolo P indica l'insieme delle parti; il simbolo A indica l'insieme a cui ci si riferisce; nel nostro caso A sono i primi 3 giorni della settimana.
Per elencazione l'insieme delle parti di A Ŕ:
PA = {ě; {lunedý, martedý, mercoledý}; {lunedý}; {martedý};{mercoledý}; {lunedý,martedý}; {lunedý, mercoledý}; {martedý, mercoledý}}
Per caratteristica l'insieme delle parti di A Ŕ:
PA = {x │ x Ŕ sottoinsieme proprio ed improprio di A}
leggiamo: l'insieme delle parti di A Ŕ uguale agli ics aventi la proprietÓ che ics Ŕ un sottoinsieme proprio ed improprio di A
Con diagramma di Venn l'insieme delle parti di A Ŕ:

L'insieme delle parti non va confuso con la partizione di un insieme.
Partizione di un insieme
Consideriamo l'insieme dei primi 3 giorni della settimana. Sia
A = {lunedý, martedý, mercoledý}
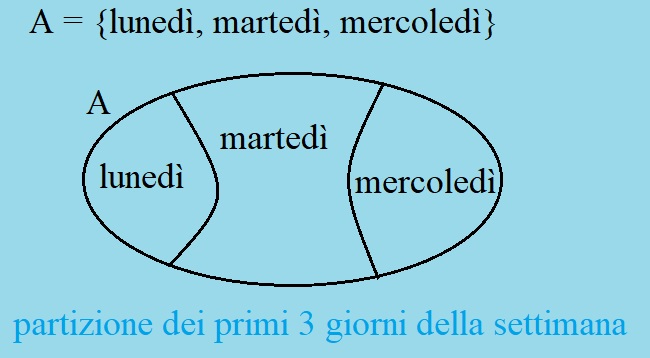
Dividiamo l'insieme A in tre parti, considerando un solo giorno; quindi, otteniamo tre sottoinsiemi propri:
B = {lunedý}
C = {martedý}
D = {mercoledý}
Gli elementi degli insiemi non sono ripetuti; mancano i due insiemi impropri, cioŔ manca l'insieme vuoto ě e l'insieme A stesso. Ho fatto una partizione dell'insieme A.
La partizione Ŕ una divisione dell'insieme in un numero di sottoinsiemi propri a piacere; inoltre la partizione deve soddisfare tre proprietÓ:
1 - nessuno degli insiemi deve essere vuoto, nÚ vi deve essere l'insieme di partenza; cioŔ tutti i sottoinsiemi devono essere propri.
2 - I sottoinsiemi non devono avere elementi in comune; cioŔ ogni elemento va considerato una sola volta.
3 - Unendo tutti i sottoinsiemi si deve ottenere l'insieme di partenza, con tutti gli elementi, nessuno escluso.
Potevamo anche dividere l'insieme A in due parti.
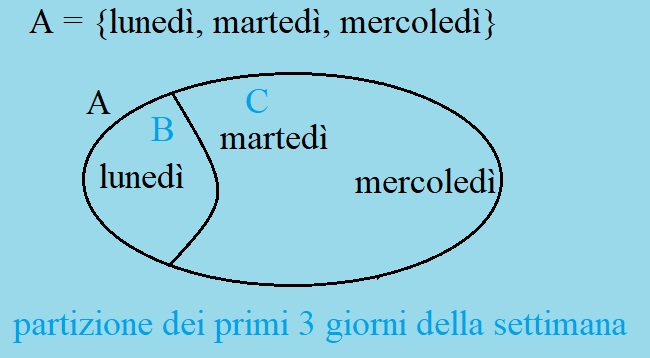
La partizione ora contiene due sottoinsiemi propri:
quindi, otteniamo due sottoinsiemi propri:
B = {lunedý}
C = {martedý, mercoledý}
Insiemi disgiunti
Due insiemi A e B si dicono disgiunti se non hanno elementi in comune;cioŔ un elemento appartiene ad uno solo degli insiemi considerati.
Considero ora sempre i primi tre giorni della settimana ma in questo modo.
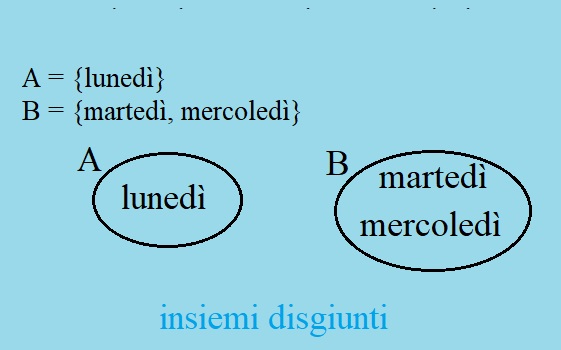
A = {lunedý}
B = {martedý, mercoledý}
I due insiemi A e B non hanno alcun elemento in comune; i due insiemi si dicono disgiunti.
Nella partizione degli insiemi, tutti i sottoinsiemi sono disgiunti; invece nell'insieme delle parti i sottoinsiemi non sono disgiunti, in quanto alcuni sottoinsiemi hanno elementi in comune.
Unione di insiemi
L'unione di due insiemi Ŕ un altro insieme che contiene tutti gli elementi dei due insiemi.
Dati due insiemi A e B.
A = {lunedý, martedý, mercoledý}
B = {giovedý, venerdý, sabato, domenica}
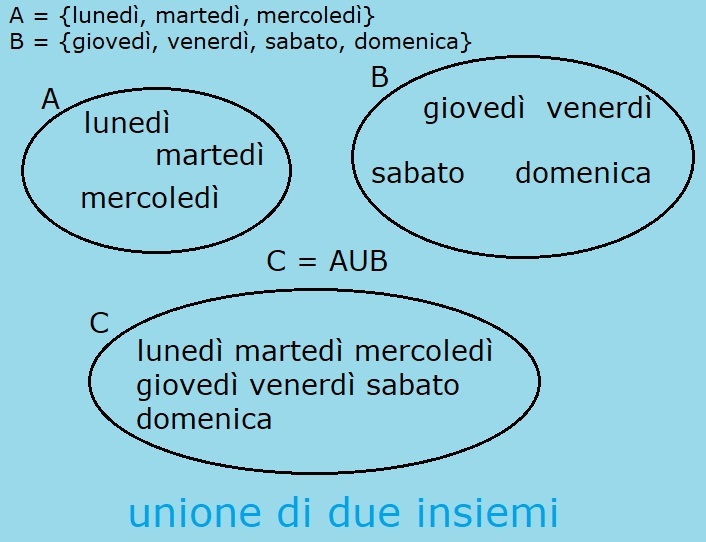
L'insieme A ha come elementi i primi tre giorni della settimana; descrivendo l'insieme A per caratteristica ho:
A = {x │ x Ŕ uno dei primi 3 giorni della settimana}
leggo: A Ŕ uguale agli x che hanno la proprietÓ che x Ŕ uno dei primi 3 giorni della settimana.
L'insieme B ha come elementi gli ultimi quattro giorni della settimana; descrivendo l'insieme B per caratteristica ho:
B = {x │ x Ŕ uno degli ultimi 4 giorni della settimana}
Nell'unione dei due insieme ottengo un altro insieme che indico con C; il simbolo dell'unione Ŕ la lettera U maiuscola stampatello.
C = AUB
leggo: C Ŕ uguale ad A unione B
Per fare l'unione devo prendere tutti gli elementi di A e tutti gli elementi di B, una sola volta; quindi C Ŕ per elencazione:
C = {lunedý, martedý, mercoledý, giovedý, venerdý, sabato, domenica}
Mentre per caratteristica C Ŕ:
C = {x │ x Ŕ uno dei 7 giorni della settimana}
oppure:
C = {x │ x Ŕ un giorno della settimana}
leggo: C Ŕ uguale agli x che hanno la proprietÓ che x Ŕ un giorno della settimana.
Nel fare l'unione dei due insiemi devo prendere gli elementi comuni e non comuni dei due insiemi, ma una sola volta.
Esempio
Dati due insiemi A e B.
A = {lunedý, martedý, mercoledý, giovedý}
B = {giovedý, venerdý, sabato, domenica}
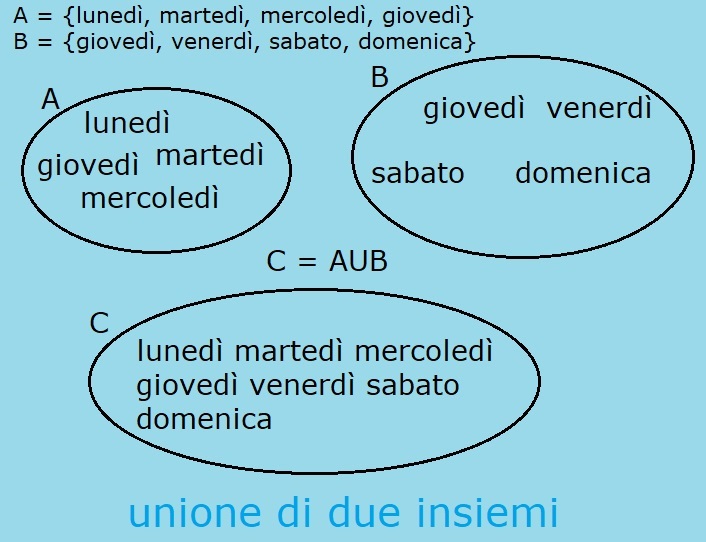
L'insieme A ha come elementi i primi 4 giorni della settimana; descrivendo l'insieme A per caratteristica ho:
A = {x │ x Ŕ uno dei primi 4 giorni della settimana}
L'insieme B ha come elementi gli ultimi quattro giorni della settimana; descrivendo l'insieme B per caratteristica ho:
B = {x │ x Ŕ uno degli ultimi 4 giorni della settimana}
Notiamo che il giorno giovedý Ŕ un elemento sia di A sia di B. Nel fare l'unione:
C = AUB
leggo: C Ŕ uguale ad A unione B
il giorno giovedý lo prendo una volta sola, anche se appartiene sia ad A sia a B.
C = {lunedý, martedý, mercoledý, giovedý, venerdý, sabato, domenica}
Mentre per caratteristica C Ŕ:
C = {x │ x Ŕ un giorno della settimana}
leggo: C Ŕ uguale agli x che hanno la proprietÓ che x Ŕ un giorno della settimana.
Attenzione a non confondere il concetto di unione con il concetto di somma; se avessi fatto la somma dei due insiemi, giovedý avrei dovuto prenderlo due volte; mentre nell'unione degli insiemi un elemento non va mai ripetuto, cioŔ va preso una sola volta.
Intersezione di insiemi
Si dice intersezione di insiemi un insieme che contiene solo gli elementi comuni ai due insiemi, presi sempre una sola volta. Il simbolo della intersezione Ŕ:
![]()
Una specie di U capovolta e si legge: intersezione.
Dati due insiemi A e B.
A = {lunedý, martedý, mercoledý, giovedý}
B = {giovedý, venerdý, sabato, domenica}
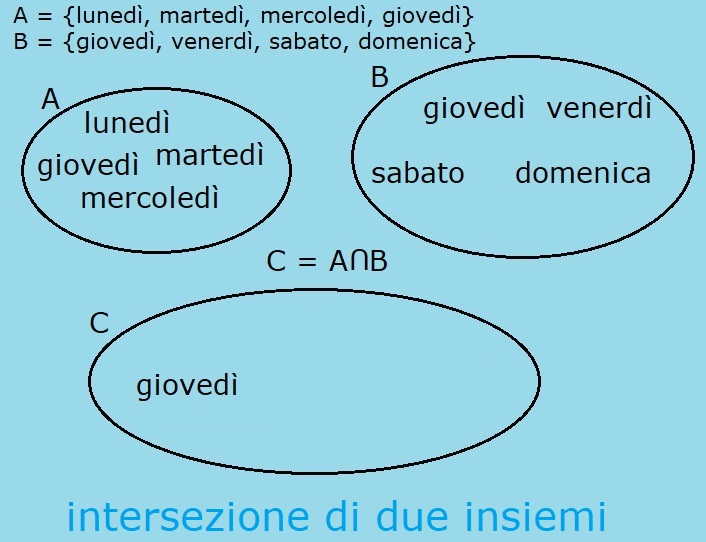
L'insieme A ha come elementi i primi 4 giorni della settimana; descrivendo l'insieme A per caratteristica ho:
A = {x │ x Ŕ uno dei primi 4 giorni della settimana}
L'insieme B ha come elementi gli ultimi quattro giorni della settimana; descrivendo l'insieme B per caratteristica ho:
B = {x │ x Ŕ uno degli ultimi 4 giorni della settimana}
Notiamo che il giorno giovedý Ŕ un elemento sia di A sia di B. Nel fare l'intersezione dei due insiemi:
C = A
![]() B
B
leggo: C Ŕ uguale ad A intersezione B
noto che il giorno giovedý Ŕ l'unico elemento che appartiene sia ad A sia a B. Lo prendo una volta sola, quindi per elencazione ottengo:
C = {giovedý}
Mentre per caratteristica C Ŕ:
C = {x │ x Ŕ un giorno della settimana che appartiene sia ad A sia a B}
leggo: C Ŕ uguale agli x che hanno la proprietÓ che x Ŕ un giorno della settimana che appartiene sia ad A sia a B.
Posso anche scrivere:
C = {x │ x
![]() A
e x
A
e x
![]() B}
B}
leggo: C Ŕ uguale agli x che hanno la proprietÓ che x appartiene ad A e x appartiene a B.
Riepilogando:
A
![]() B
= C = {x │ x
B
= C = {x │ x
![]() A
e x
A
e x
![]() B}
B}
leggo: la intersezione di A e B Ŕ uguale a C; Ŕ uguale agli x che hanno la proprietÓ che x appartiene appartiene ad A e x appartiene a B.
A volte il diagramma degli insiemi, detto diagramma di Venn, viene fatto in questo modo:
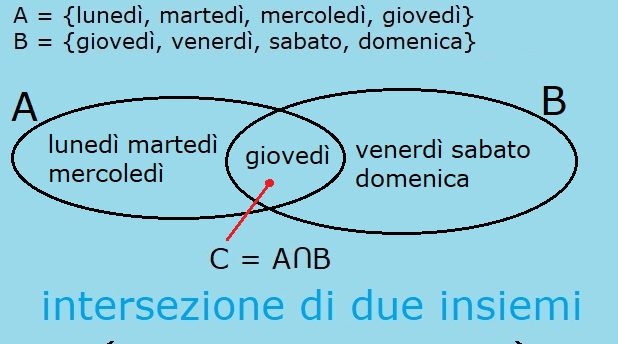
Casi particolari di intersezione
Se due insiemi non hanno elementi in comune, la intersezione di A e B Ŕ l'insieme vuoto.
A
![]() B = ě
B = ě
I due insiemi si dicono disgiunti, in quanto non hanno elementi in comune.
Esempio
A = {gennaio, febbraio, marzo, aprile, maggio, giugno, luglio, agosto, settembre, ottobre, novembre, dicembre} = {x │ x Ŕ un mese dell'anno}
B = {lunedý, martedý, mercoledý, giovedý, venerdý, sabato, domenica} = {x │ x Ŕ un giorno della settimana}
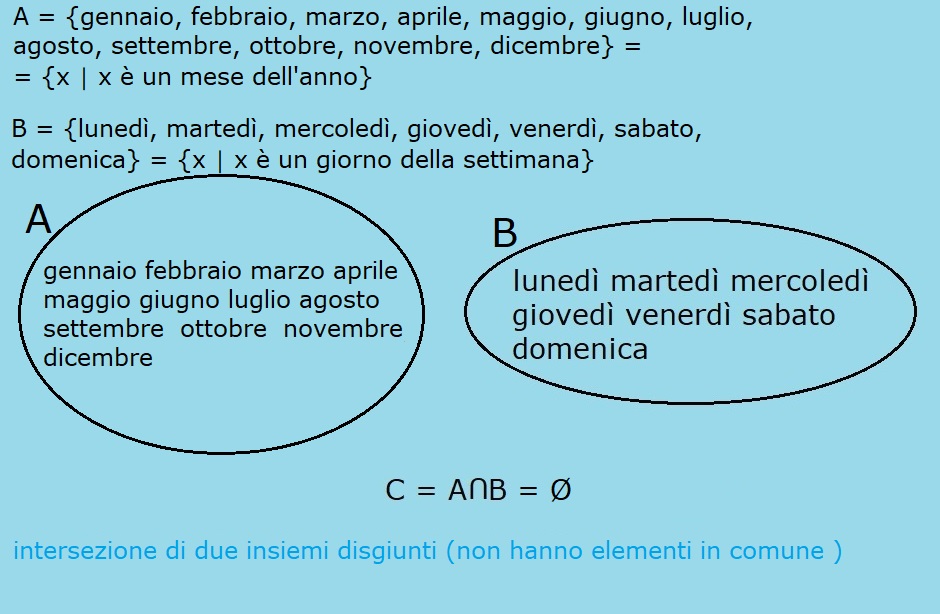
I due insiemi non hanno elementi in comune; la intersezione di A e B Ŕ l'insieme vuoto.
A
![]() B = ě
B = ě
I due insiemi si dicono disgiunti, in quanto non hanno elementi in comune.
Un altro caso particolare si ha quando l'insieme B Ŕ contenuto in A.
Sia:
A = {lunedý, martedý, mercoledý, giovedý, venerdý, sabato, domenica} = {x │ x Ŕ un giorno della settimana}
B = {domenica} = {x │ x Ŕ un giorno festivo della settimana}
I due insiemi hanno un solo elemento in comune, cioŔ domenica; la intersezione di A e B Ŕ l'insieme B stesso.
A
![]() B = {domenica} = B
B = {domenica} = B
In questo caso B Ŕ contenuto in A
B
![]() A
A
leggiamo: B contenuto in A.
B Ŕ un sottoinsieme proprio di A.
Differenza di insiemi
La differenza tra due insiemi A e B si ottiene togliendo da A tutti gli elementi di B; si ottiene in tal modo un nuovo insieme, detto insieme differenza, che Ŕ costituito dagli elementi di A che non appartengono anche a B. Il simbolo della differenza Ŕ il segno meno - oppure il segno \, che leggo: meno.
Quindi scrivo:
C = A-B
e leggo:
C uguale ad A meno B
oppure leggo:
C uguale A differenza B.
Posso anche scrivere:
C = A \ B
e leggo:
C uguale ad A meno B
oppure leggo:
C uguale A differenza B.
Esempio
Dati due insiemi A e B.
A = {lunedý, martedý, mercoledý, giovedý}
B = {giovedý, venerdý, sabato, domenica}
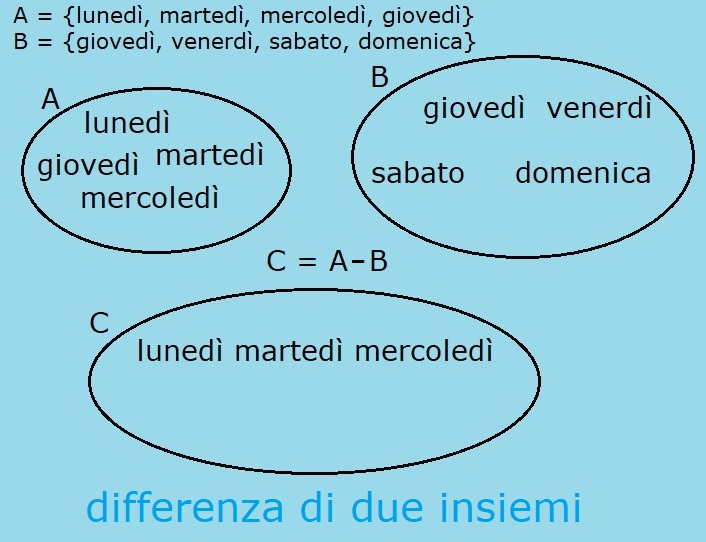
L'insieme A ha come elementi i primi 4 giorni della settimana; descrivendo l'insieme A per caratteristica ho:
A = {x │ x Ŕ uno dei primi 4 giorni della settimana}
leggo: A Ŕ uguale agli x che hanno la proprietÓ che x Ŕ uno dei primi 4 giorni della settimana.
L'insieme B ha come elementi gli ultimi quattro giorni della settimana; descrivendo l'insieme B per caratteristica ho:
B = {x │ x Ŕ uno degli ultimi 4 giorni della settimana}
Nella differenza dei due insieme ottengo un altro insieme che indico
con C; noto che non Ŕ come la differenza tra numeri, nella quale il sottraendo,
cioŔ il secondo numero, deve essere pi¨ piccolo del minuendo, cioŔ del primo
numero, che Ŕ sempre pi¨ grande. Nella differenza tra due insiemi tolgo solo gli
elementi del secondo insieme che sono anche elementi del primo insieme, che poi
sono gli elementi di A
![]() B.
B.
Noto, quindi, che solo giovedý appartiene sia ad A sia a B. Quindi dall'insieme A tolgo solo giovedý ed ottengo:
C = A - B = {lunedý, martedý, mercoledý, giovedý} - {giovedý, venerdý, sabato, domenica} = {lunedý, martedý, mercoledý}
Posso anche fare:
C = B - A = {giovedý, venerdý, sabato, domenica} - {lunedý, martedý, mercoledý, giovedý} = {venerdý, sabato, domenica}
Questa volta ho tolto giovedý dall'insieme B, essendo l'unico elemento in comune.
Casi particolari
Un caso particolare Ŕ quando B Ŕ sottoinsieme di A, cioŔ:
B
![]() A
A
leggiamo: B contenuto in A.
In questo caso l'insieme differenza, cioŔ
C = A - B
si chiama insieme complementare di B rispetto ad A e si indica in questo modo:
CA B = A - B
Esempio
Dati due insiemi A e B.
A = {lunedý, martedý, mercoledý, giovedý, venerdý, sabato, domenica}
B = {giovedý, venerdý, sabato, domenica}
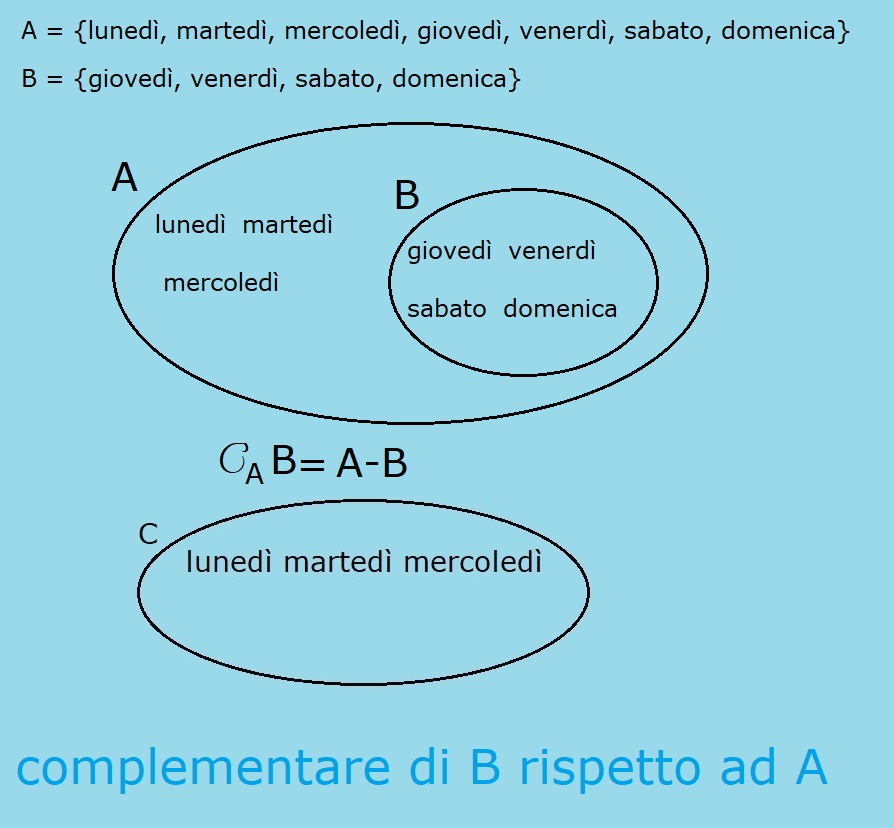
L'insieme complementare di B rispetto ad A Ŕ:
CA B = A - B = {lunedý, martedý, mercoledý}
Ho tolto da A tutto l'insieme B.
prof. Pietro De Paolis
Corso di matematica per scuola media
|
|
Indice di tutte le pagine del sito