| data di oggi: |
La bella geometria
 |
|
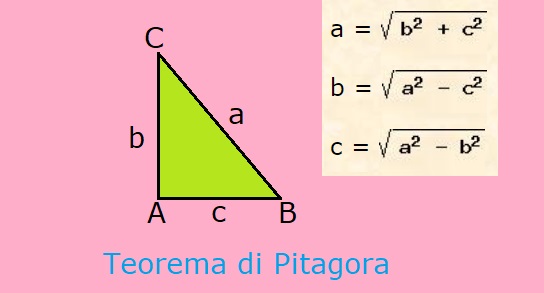
triangolo rettangolo |
Consideriamo il triangolo ABC, è un triangolo rettangolo, avendo un angolo di 90 gradi nel vertice A.
Indichiamo con la lettera a minuscola il lato opposto al vertice A; questo lato si chiama ipotenusa.
Indichiamo con la lettera b minuscola il lato opposto al vertice B; questo lato si chiama cateto.
Indichiamo con la lettera c minuscola il lato opposto al vertice C; anche questo lato si chiama cateto.
Quindi i lati più piccoli si chiamano cateti; il lato più lungo si chiama ipotenusa.
Le formule del Teorema di Pitagora sono le seguenti.
a =
b =
c =
La formula:
a =si legge a uguale radice quadrata del quadrato di b più il quadrato di c.
Esempio
Un triangolo rettangolo ha un cateto di 3 cm; un altro cateto è di 4 cm.
Calcola l'ipotenusa.
Svolgimento
 |
|
triangolo ABC |
Ricordando la formula:
a =Sostituisco i valori nella formula:
a =Risposta
La ipotenusa a del triangolo rettangolo misura 5 cm.
La formula:
c =si legge c uguale radice quadrata del quadrato di a meno il quadrato di b.
Esempio
Un triangolo rettangolo ha un cateto di 3 cm; l'ipotenusa è di 5 cm.
Calcola l'altro cateto.
Svolgimento
 |
|
triangolo ABC |
Ricordando la formula:
c =Sostituisco i valori nella formula:
c =Risposta
Il cateto c del triangolo rettangolo misura 4 cm.
Le formule:c =
b =
sono simili, nel senso che possiamo scambiare i cateti tra di loro, cioè cateto b con cateto c.
Esempio
Un triangolo rettangolo ha un cateto di 4 cm; l'ipotenusa è di 5 cm.
Calcola l'altro cateto.
Svolgimento
 |
|
triangolo rettangolo ABC |
Ricordando la formula:
b =Sostituisco i valori nella formula:
b =Risposta
Il cateto b del triangolo rettangolo misura 3 cm.
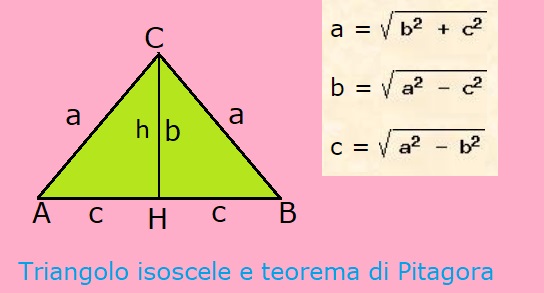
Triangolo isoscele e teorema di Pitagora
Il teorema di Pitagora si può usare per calcolare i lati e l'altezza del triangolo isoscele.
 |
|
triangolo isoscele ABC |
Disegno l'altezza h di un triangolo isoscele. L'altezza divide il triangolo isoscele in due triangoli rettangoli aventi la stessa superficie; si dice che i due triangoli rettangoli sono congruenti, cioè hanno la stessa area.
Il lato del triangolo isoscele coincide con la ipotenusa; l'altezza del triangolo isoscele coincide con il cateto b del triangolo rettangolo; il cateto c è congruente a metà base del triangolo isoscele.
Esempio
Un triangolo isoscele ha la base di 6 cm; il lato obliquo è lungo 5 cm. Calcolare l'altezza del triangolo isoscele.
Svolgimento del problema
Dati:
Poligono: triangolo isoscele ABC
base AB = 6 cm
lato obliquo BC = 5 cm
Calcolo metà base sapendo che:
base = 6 cm
divisore = 2
Applico la formula:
metà base =
ed ottengo:
metà base =
= 3 cm
Risposta
metà base è 3 cm
Dati:
Poligono: triangolo rettangolo HBC
cateto c = HB = 3 cm
ipotenusa a = BC = 5 cm
Soluzione
Si richiede un cateto di un triangolo rettangolo HBC avente:
cateto c = HB = metà base = 3 cm
ipotenusa a = BC = lato obliquo = 5 cm
Applico la formula derivata dal teorema di Pitagora:
cateto b = CH = altezza = Va² - c² ed ottengo:
cateto b = V(5 cm)² - (3 cm)² = 4 cm
Risposta
L'altro cateto b = CH del triangolo rettangolo HBC, che coincide con altezza del
triangolo isoscele, è
4 cm.
Esempio
Un triangolo isoscele ha la base di 6 cm; l'altezza è lunga 4 cm. Calcolare il lato obliquo.
Svolgimento del problema
Dati:
Poligono: triangolo isoscele ABC
base AB = 6 cm
altezza CH = 4 cm
Calcolo metà base sapendo che:
base = 6 cm
divisore = 2
Applico la formula:
metà base =
ed ottengo:
metà base =
= 3 cm
Risposta
metà base è 3 cm
Dati:
Poligono: triangolo rettangolo HBC
cateto b = CH = 4 cm
cateto c = HB = 3 cm
Soluzione
Si richiede l'ipotenusa di un triangolo rettangolo HBC avente:
cateto b = CH = altezza = 4 cm
cateto c = HB = metà base = 3 cm
Applico la formula del teorema di Pitagora:
ipotenusa a = BC = V b² + c² ed ottengo:
a = V(4 cm)² + (3 cm)² = 5 cm
Risposta
L'ipotenusa del triangolo rettangolo HBC, che coincide con lato obliquo del
triangolo isoscele, è 5 cm.
prof. Pietro De Paolis
Corso di matematica per scuola media
|
|

















