La bella geometria - Cerchio inscritto nel rombo

Rombo circoscritto al cerchio parte 5 su 5

data di oggi:

Classe 2^a della scuola media


Zitto!	Parla!

La bella geometria

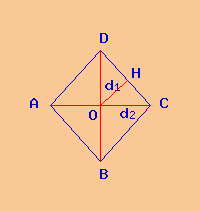
rombo

Consideriamo un rombo, esso ha le due diagonali di lunghezza diversa, per cui non esiste un cerchio in grado di circoscrivere un rombo, cioè un cerchio che contiene il rombo stesso.

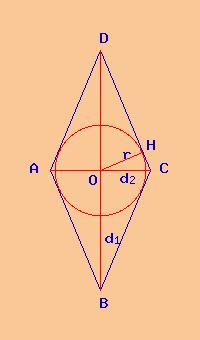
rombo circoscritto al cerchio

Avendo il rombo le somme dei lati opposti uguali a due a due, il rombo può essere circoscritto al cerchio, cioè esiste un cerchio che può essere iscritto nel rombo. Ci possiamo quindi calcolare il raggio del cerchio; il raggio del cerchio inscritto è detto anche apotema ( nome maschile singolare).

cerchio inscritto e triangolo OCD

Dalla figura notiamo che il raggio è uguale all'altezza del triangolo OCD rispetto al lato DC.

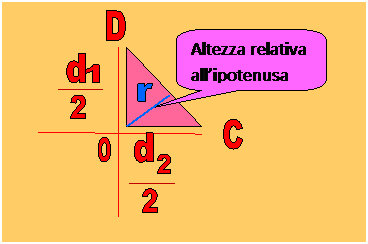raggio = altezza relativa all'ipotenusa del triangolo OCD

Per cui se conosco l'area del triangolo OCD posso calcolarmi l'altezza relativa all'ipotenusa con la formula:

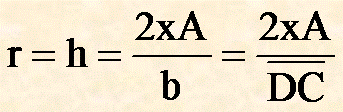
Esempio

Un rombo ha l'area di 864 cm² e il lato di 30 cm.

Calcolare il raggio del cerchio inscritto nel rombo.

Svolgimento

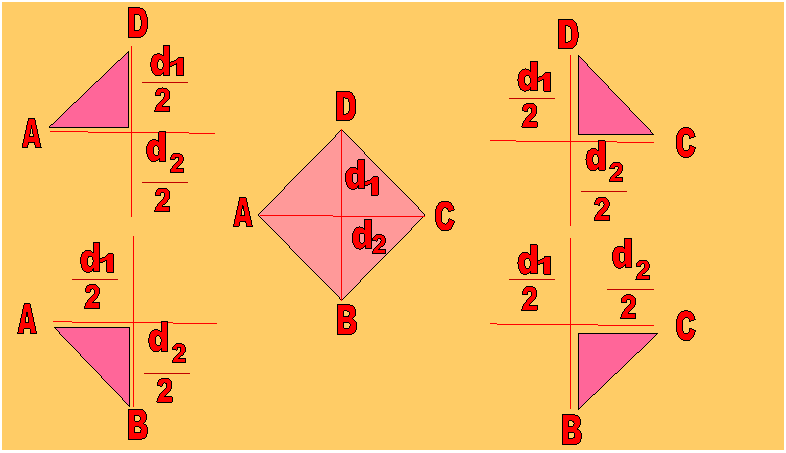
rombo = 4 triangoli rettangoli

Ricordando che il rombo è congruente alla somma di 4 triangoli rettangoli, divido l'area del rombo in 4 parti ed ottengo l'area del triangolo rettangolo OCD:

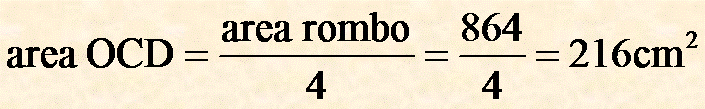
Poi applico la formula:

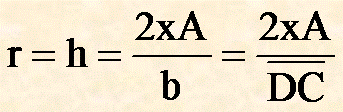
dove A = area del triangolo ed ottengo:

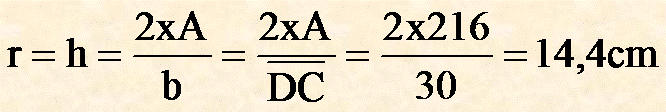
Risposta

Il raggio r del cerchio inscritto nel rombo è lungo 14,4 cm.

Controlliamo con la rombocalcolatrice:

http://www.scuolaelettrica.it/php/risolutore/rombo.php?funzione=raggiorombocirco(48,36,cm,ABCD

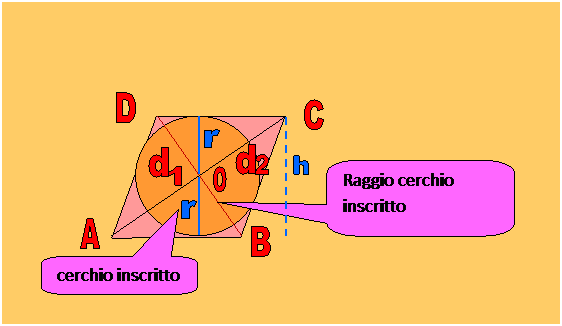
raggio = metà altezza del rombo

Dalla figura notiamo che il diametro del cerchio inscritto nel rombo è congruente all'altezza h del rombo rispetto ad un suo lato. Di conseguenza se conosco l'area A del rombo e un lato mi calcolo dapprima h con la formula:

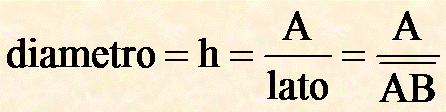
poi divido il diametro in 2 parti ed ottengo il raggio:

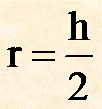
Esempio

Un rombo ha l'area di 864 cm² e il lato di 30 cm.

Calcolare il raggio del cerchio inscritto nel rombo.

Svolgimento

Ricordando la formula:

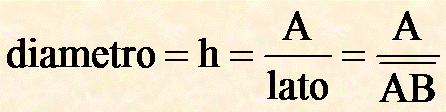
metto i valori ed ottengo il diametro:

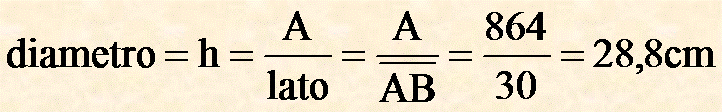
poi divido in due parti ed ottengo il raggio:

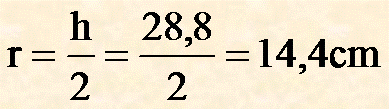
Risposta

Il raggio r del cerchio inscritto nel rombo è lungo 14,4 cm.

Un altro modo è quello di usare la formula valida per tutti i poligoni regolari cioè:

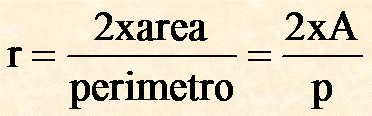
il raggio del cerchio inscritto è uguale al doppio dell'area diviso il perimetro.

Esempio

Un rombo ha l'area di 864 cm² e il perimetro di 120 cm.

Calcolare il raggio del cerchio inscritto nel rombo.

Svolgimento

Ricordando la formula:

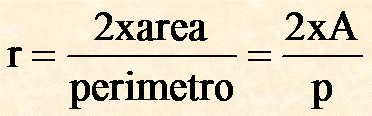
metto i valori ed ottengo il raggio:

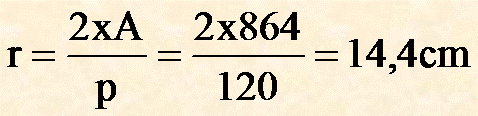
Risposta

Il raggio r del cerchio inscritto nel rombo è lungo 14,4 cm.

Controlliamo con la rombocalcolatrice:

http://www.scuolaelettrica.it/php/risolutore/rombo.php?funzione=raggiorombocirco2(864,120,cm,ABCD

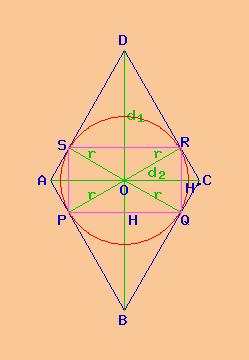
rombo e corde del cerchio inscritto

Dalla figura notiamo che il cerchio inscritto nel rombo incontra i quattro lati nei punti di tangenza P, Q, R ed S. Unendo i quattro punti di tangenza si ottiene un triangolo rettangolo PQRS. Inoltre vi sono quattro corde del cerchio:

corda PQ che dista OH dal centro O;

corda SR =PQ che dista OH dal centro O;

corda PS che dista OH' dal centro O;

corda QR = PS che dista OH' dal centro O;

Possiamo anche considerare 4 angoli al centro:

angolo PÔQ = angolo SÔR

angolo PÔS = angolo QÔR

Conoscendo le diagonali il lato e il raggio del cerchio inscritto nel rombo ci possiamo calcolare le 4 corde, le loro distanze dal centro e i 4 angoli al centro.

Esempio

Un rombo ha le diagonali rispettivamente di 48 cm e 36 cm; il lato è lungo 30 cm e il raggio del cerchio inscritto è di 14,4 cm.

Calcolare le corde, le loro distanze dal centro O, i quattro angoli al centro e la lunghezza dei corrispondenti archi di circonferenza.

Svolgimento

Considero il triangolo rettangolo PBO; noto che il segmento PH, pari a metà corda PQ, è congruente all'altezza h relativa all'ipotenusa OB.

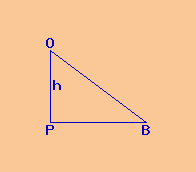
Mi calcolo il cateto PB del triangolo rettangolo PBO applicando il teorema di Pitagora

cateto PB = V OB ² - OP² ed ottengo:

cateto PB = V(24 cm)² - (14,4 cm)² = 19,2 cm

Calcolo l'area del triangolo PBO avente:
base PB = 19,2 cm
altezza h = OP = 14,4 cm
applico la formula A = ed ottengo:

A = = 138,24 cm²

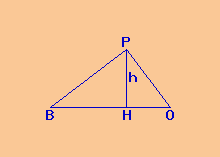
Calcolo segmento PH, pari a metà corda PQ, essendo congruente all'altezza h relativa all'ipotenusa del triangolo BOP.
Si richiede segmento PH di un triangolo BOP avente:
base OB = 24 cm
area A =138,24 cm²
Applico la formula:
PH = ed ottengo:
PH = = 11,52 cm

Il segmento PH è congruente alla distanza della corda PS dal centro O del cerchio inscritto nel rombo ABCD.

Calcolo la corda PQ moltiplicando per 2 il segmento PH. Ottengo:
PQ = 2 x PH = 2 x 11,52 = 23,04 cm

Risposta
La corda PQ del cerchio inscritto nel rombo ABCD è 23,04 cm.

Per calcolare la distanza OH della corda PQ dal centro O considero il triangolo rettangolo HOP.

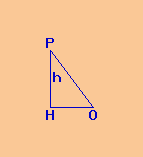
Mi calcolo il cateto OH del triangolo rettangolo HOP applicando il teorema di Pitagora

cateto OH = V OP² - PH² ed ottengo:

cateto OH = V(14,4 cm)² - (11,52 cm)² = 8,64 cm
Il segmento OH è congruente alla distanza della corda PQ dal centro O del cerchio inscritto nel rombo ABCD.

Calcolo la corda PS moltiplicando per 2 il segmento OH. Ottengo:
PS = 2 x OH = 2 x 8,64 = 17,28 cm

Risposta
La corda PS del cerchio inscritto nel rombo ABCD è 17,28 cm.
cm.

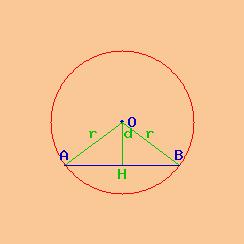
Figura geometrica: circonferenza
raggio r = 14,4 cm
corda AB = 23,04 cm
Soluzione

Si richiede l'angolo al centro AÔB = α ( alfa ) di una circonferenza avente:
raggio r = 14,4 cm
corda AB = 23,04 cm
Applico il teorema della corda:
corda AB = 2 x r x sen

da cui:
sen =

da cui:

= arcsen = arcsen =

53,130102354156 °

da cui:
α = 2 x = 2 x 53,130102354156 =

106,26020470831°

Risposta
L'angolo al centro AÔB sotteso dalla corda AB è 106,26020470831 °

Converto 106,26020470831 da grado decimale a grado sessagesimale
Moltiplico la parte decimale di 106,26020470831 per 60 = 0,26020470831 x 60 = 15.6122824986
prendo la parte intera ed ottengo 15'
Moltiplico la parte decimale di 15.6122824986 per 60 = 0,6122824986 x 60 = 36.736949916
prendo la parte intera arrotondata ed ottengo 37''

Ho convertito da 106,26020470831 gradi decimali a 106° 15' 37'' gradi sessagesimali.

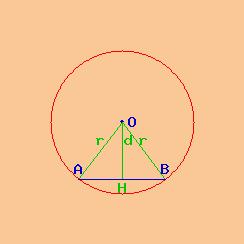
Figura geometrica: circonferenza
raggio r = 14,4 cm
corda AB = 17,28 cm
Soluzione

Si richiede l'angolo al centro AÔB = α ( alfa ) di una circonferenza avente:
raggio r = 14,4 cm
corda AB = 17,28 cm
Applico il teorema della corda:
corda AB = 2 x r x sen

da cui:

sen =

da cui:

= arcsen = arcsen =

36,869897645844 °

da cui:

α = 2 x = 2 x 36,869897645844 =

73,739795291688°

Risposta
L'angolo al centro AÔB sotteso dalla corda AB è 73,739795291688 °

Converto 73,739795291688 da grado decimale a grado sessagesimale
Moltiplico la parte decimale di 73,739795291688 per 60 = 0,739795291688 x 60 = 44.38771750128
prendo la parte intera ed ottengo 44'
Moltiplico la parte decimale di 44.38771750128 per 60 = 0,38771750128 x 60 = 23.2630500768
prendo la parte intera arrotondata ed ottengo 23''

Ho convertito da 73,739795291688 gradi decimali a 73° 44' 23'' gradi sessagesimali.

Calcolo degli archi di circonferenza
Converto 106° 15' 37'' da grado sessagesimale a numero decimale in gradi
divido 15' per 60 ed ottengo: = 0,25 in decimale

divido 37'' per 3600 ed ottengo: = 0,010277777777778 in decimale

Sommo: 106 + 0,25 + 0,010277777777778 = 106,26027777778 in ° decimali

Ho convertito 106° 15' 37'' da gradi sessagesimali a 106,26027777778 gradi decimali

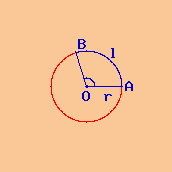
Dati
Figura geometrica: circonferenza
raggio r = 14,4 cm
angolo α = 106,26027777778 °
Soluzione
Si richiede la lunghezza dell'arco l corrispondente all'angolo α di una circonferenza il cui raggio è:
r = 14,4 cm
Applico la formula:

arco l =

ed ottengo:

arco l = =

26,706098085112 cm = 8,5008222222224 π cm

Risposta
L'arco l è lungo 26,706098085112 cm

Calcolo gli altri due archi di circonferenza

Converto 73° 44' 23'' da grado sessagesimale a numero decimale in gradi
divido 44' per 60 ed ottengo: =

0,73333333333333 in decimale

divido 23'' per 3600 ed ottengo: =

0,0063888888888889 in decimale

Sommo: 73 + 0,73333333333333 + 0,0063888888888889 = 73,739722222222 in ° decimali

Ho convertito 73° 44' 23'' da gradi sessagesimali a 73,739722222222 gradi decimali

Dati
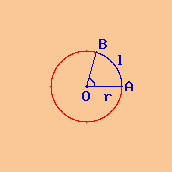
Figura geometrica: circonferenza
raggio r = 14,4 cm
angolo α = 73,739722222222 °
Soluzione
Si richiede la lunghezza dell'arco l corrispondente all'angolo α di una circonferenza il cui raggio è:
r = 14,4 cm
Applico la formula:

arco l =

ed ottengo:

arco l = =

18,532797914889 cm = 5,8991777777778 π cm

Risposta
L'arco l è lungo 18,532797914889 cm

Javascript

Possiamo costruire un programma in javascript che calcola il raggio del cerchio inscritto nel rombo sapendo le due diagonali; basta semplicemente passare i valori esatti alla pagina di Scuola Elettrica, seguendo le istruzioni riportate alla pagina:

http://www.scuolaelettrica.it/php/risolutore/rombo.php

Modulo da costruire