La bella geometria - Arco, angolo al centro, angoli alla circonferenza

Angolo al centro e angoli alla circonferenza parte 2 su 5

data di oggi:

Classe 2^a della scuola media


Zitto!	Parla!

La bella geometria


circonferenza	cerchio

Angolo al centro

Consideriamo una circonferenza e due punti A e B appartenenti ad essa.

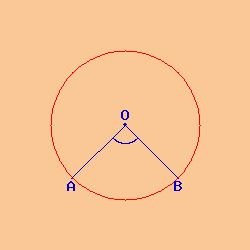angolo al centro

Se uniamo con un segmento il punto A con il centro O della circonferenza ed il punto B sempre con il centro O notiamo un angolo AÔB che è detto angolo al centro, in quanto è riferito al centro della circonferenza.

La parte di circonferenza compresa tra A e B è detta arco AB. La lunghezza dell'arco AB di solito la indichiamo con la lettera l minuscola.

Tra lunghezza dell'arco e l'angolo al centro esiste una proporzionalità diretta, nel senso che maggiore è l'angolo al centro maggiore è la lunghezza dell'arco; infatti l'arco è una parte della circonferenza. Quando l'angolo al centro è 360° l'arco è lungo quanto la circonferenza.

angolo al centro	lunghezza arco	rapporto con la circonferenza
360°	l=2·3,14 ·r	intera circonferenza
180°		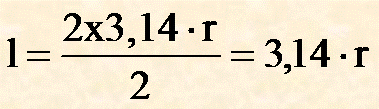metà circonferenza
90°		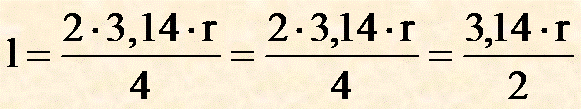un quarto di circonferenza
270°		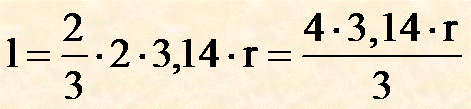due terzi di circonferenza

In generale la formula per calcolare la lunghezza dell'arco è la seguente:

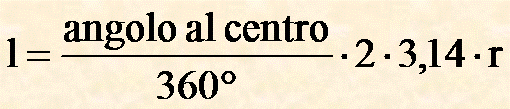
Esempio

Una circonferenza è lunga 20 π cm: Calcola la lunghezza dell'arco AB sapendo che l'angolo al centro AÔB è di 90°.

Svolgimento

Applico la formula:

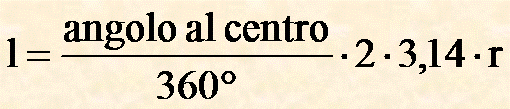
Ricordando che la lunghezza della circonferenza è:

c = 2· 3,14 ·r = 20 π cm

Metto i valori ed ottengo:

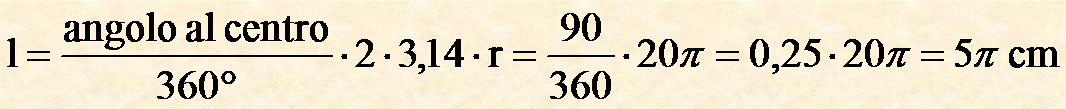
Risposta

L'arco l è lungo 5π cm.

Controlliamo con la cerchiocalcolatrice:

http://www.scuolaelettrica.it/php/risolutore/cerchio.php?funzione=arcosettoreangolocirconferenza(90,20 pigreca,cm

Angolo alla circonferenza

Consideriamo una circonferenza e due punti A e B appartenenti ad essa.

angoli alla circonferenza

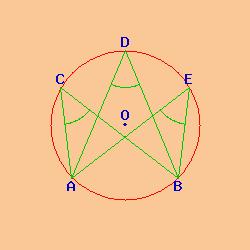
Se uniamo con un segmento il punto A con un punto C della circonferenza ed il punto B sempre con lo stesso punto C notiamo un angolo AĈB che è detto angolo alla circonferenza, in quanto è riferito ad un punto della circonferenza.

Se al posto del punto C scegliamo un altro punto E della circonferenza si ottiene un altro angolo alla circonferenza AÊB che ha la stessa ampiezza dell'angolo AĈB.

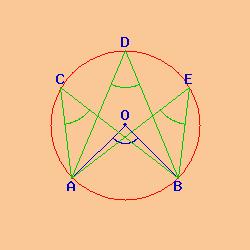
Infatti tutti gli angoli alla circonferenza sottesi dallo stesso arco AB sono tra loro uguali. Inoltre l'ampiezza di un angolo alla circonferenza è esattamente la metà del corrispondente angolo al centro.

angoli al centro e angoli alla circonferenza

e di conseguenza un angolo al centro è pari al doppio di ogni angolo alla circonferenza, sempre se consideriamo lo stesso arco AB.

Esempio

Un angolo al centro AÔB è di 90°.

Calcolare l'angolo alla circonferenza sotteso dallo stesso arco.

Svolgimento

Ricordando che un angolo alla circonferenza è pari alla metà dell'angolo al centro sotteso dallo stesso arco ottengo:

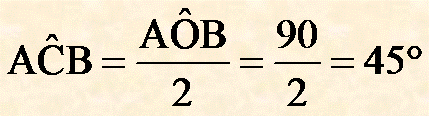
Risposta

L'angolo alla circonferenza AĈB è ampio 45°.

Controlliamo con la cerchiocalcolatrice:

http://www.scuolaelettrica.it/php/risolutore/cerchio.php?funzione=angolocirconferenza(90,10)

Javascript

Possiamo costruire un programma in javascript che calcola la lunghezza di un arco sapendo l'ampiezza dell'angolo al centro corrispondente e il raggio della circonferenza; basta semplicemente passare i valori esatti alla pagina di Scuola Elettrica, seguendo le istruzioni riportate alla pagina:

http://www.scuolaelettrica.it/php/risolutore/cerchio.php

Modulo da costruire