Settore circolare, segmento circolare, corona circolare

Settore circolare, segmento circolare, corona circolare parte 3 su 3

data di oggi:

Classe 2^a della scuola media


Zitto!	Parla!

La bella geometria


circonferenza	cerchio

Settore circolare

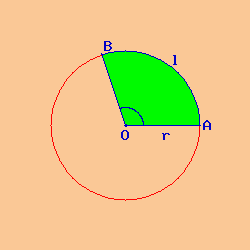
Consideriamo una circonferenza e due punti A e B appartenenti ad essa.

settore circolare

Uniamo con un segmento il punto A con il centro O della circonferenza ed il punto B sempre con il centro O; consideriamo la parte di cerchio compresa tra l'arco AB e l'angolo al centro AÔB; tale parte è detta settore circolare in quanto è una parte del cerchio. La misura della superficie del settore circolare la chiamiamo area del settore circolare e la indichiamo con A_s.

Tra l'area del settore e l'angolo al centro esiste una proporzionalità diretta, nel senso che maggiore è l'angolo al centro maggiore è l'area del settore circolare; infatti il settore è una parte di cerchio. Quando l'angolo al centro è 360° l'area del settore è pari all'area del cerchio.

angolo al centro	area del settore	rapporto con la circonferenza
360°	A_s= r ·r ·3,14	intero cerchio
180°		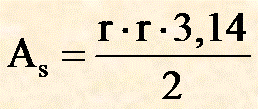metà cerchio
90°		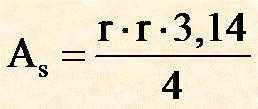un quarto di cerchio
270°		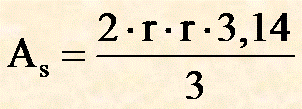due terzi di cerchio

In generale la formula per calcolare l'area del settore è la seguente:

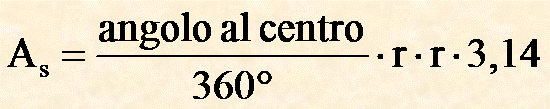
Esempio

L'area di un cerchio è 100 π cm²; Calcola l'area del settore circolare sotteso dall'arco AB sapendo che l'angolo al centro AÔB è di 90°.

Svolgimento

Applico la formula:

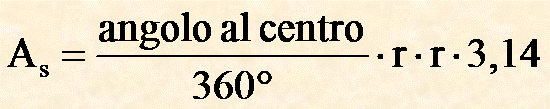
Ricordando che l'area del cerchio è:

A = r·r· 3,14 = 100 π cm²

Metto i valori ed ottengo:

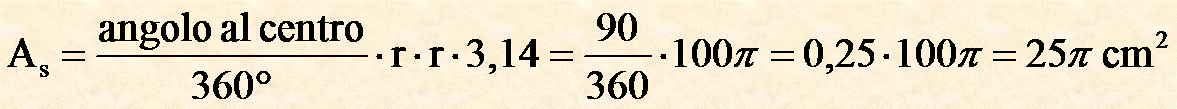
Risposta

L'area settore circolare è 25π cm².

Controlliamo con la cerchiocalcolatrice:

http://www.scuolaelettrica.it/php/risolutore/cerchio.php?funzione=areasettoreangolocerchio(90,100 pigreca,cm²)

Segmento circolare

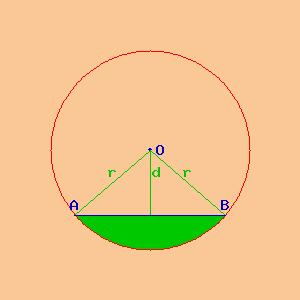
Consideriamo una circonferenza e due punti A e B appartenenti ad essa.

segmento circolare

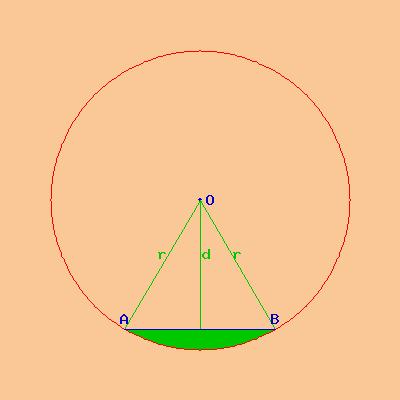
Uniamo con un segmento il punto A con il punto B; la parte di cerchio compresa tra l'arco AB e il segmento AB è detta segmento circolare. La misura della superficie del segmento circolare la chiamiamo area del segmento circolare.

La possiamo calcolare come differenza tra l'area del settore circolare A_s e l'area del triangolo isoscele AOB.

Esempio

Un cerchio ha l'area di 2827,431 cm². Calcola l'area del segmento circolare sotteso dall'arco AB sapendo che l'angolo al centro AÔB è di 60° e che il triangolo equilatero AOB ha l'area di 389,711 cm²

Svolgimento

Mi calcolo dapprima l'area del settore circolare con la formula:

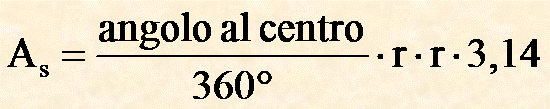
Ricordando che l'area del cerchio è:

A = r·r· 3,14 = 2827,431 cm²

Metto i valori ed ottengo:

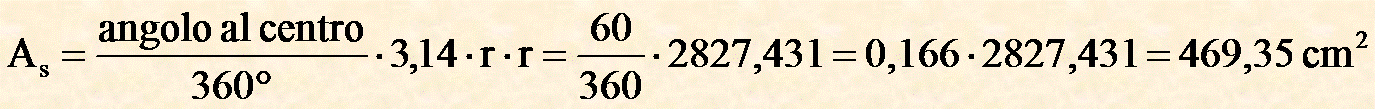
Eseguo la differenza tra l'area del settore circolare e l'area del triangolo AOB ed ottengo:
area segmento circolare = 469,35 cm² - 389,711 cm² = 79,639 cm²
Risposta
L'area del segmento circolare A_s è 79,639 cm²

Controlliamo con la cerchiocalcolatrice:

http://www.scuolaelettrica.it/php/risolutore/cerchio.php?funzione=areasegmentoangolo(60,30,cm)

Corona circolare

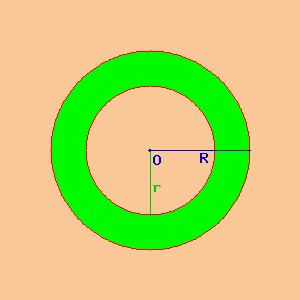corona circolare

Disegniamo due circonferenze una di raggio r ed una di raggio R, maggiore di r. La corona circolare è la parte di superficie compresa tra le due circonferenza.

Per calcolare l'area della corona basta fare la differenza tra l'area del cerchio esterno di raggio R e l'area del cerchio interno di raggio r.

Esempio

Una corna circolare ha raggio interno r = 20 cm e raggio esterno R = 30 cm. Calcola l'area della corona circolare.

Svolgimento

Calcolo dapprima l'area del cerchio esterno con la formula:
A_e = R x R x 3,14159
ed ottengo:
A_e = 30 cm x 30 cm x 3,14159 = 2827,431 cm²
Calcolo, poi, l'area del cerchio interno con la formula:
A_i = r x r x 3,14159
ed ottengo:
A_i = 20 cm x 20 cm x 3,14159 = 1256,636 cm²
Faccio la differenza tra area del cerchio esterno e l'area del cerchio interno.
Quindi:
A_c = A_e - A_i = 2827,431 - 1256,636 = 1570,795 cm² = 500 π cm²

Risposta
L'area della corona circolare è 1570,795 cm².

Controlliamo con la cerchiocalcolatrice:

http://www.scuolaelettrica.it/php/risolutore/cerchio.php?funzione=areacorona(20,30,cm)

Javascript

Possiamo costruire un programma in javascript che calcola l'area di un settore circolare sapendo l'ampiezza dell'angolo al centro corrispondente e il raggio del cerchio; basta semplicemente passare i valori esatti alla pagina di Scuola Elettrica, seguendo le istruzioni riportate alla pagina:

http://www.scuolaelettrica.it/php/risolutore/cerchio.php

Modulo da costruire