La bella geometria

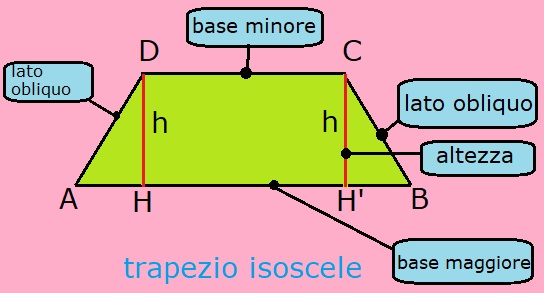
trapezio

Il trapezio ha quattro lati, quindi è un quadrilatero. I lati paralleli sono soltanto due, cioè il lato AB è parallelo al lato DC. Non è un parallelogramma; il parallelogramma ha i quattro lati paralleli a due a due. Non è un rombo, che ha i lati paralleli a due a due ed uguali.

I due lati paralleli si chiamano basi; vi sono due basi: la base maggiore AB, cioè la più lunga, e la base minore DC, cioè la più corta. Gli altri due lati non paralleli si chiamano lati obliqui.

Il segmento AH si chiama proiezione del lato obliquo.

La somma degli angoli interni è 360°, cioè (4 lati - 2) x 180° = 2 x 180° = 360°.

trapezio isoscele

Il trapezio si dice trapezio isoscele se ha i due lati obliqui della stessa lunghezza. Nel trapezio isoscele i due angoli alla base maggiore hanno la stessa misura, cioè

angolo DAB = angolo ABC.

Nel trapezio isoscele i due angoli alla base minore hanno la stessa misura, cioè

angolo ADC = angolo DCB.

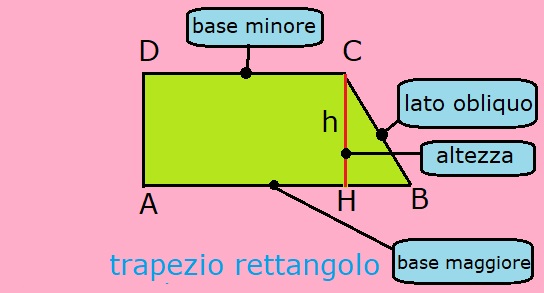
trapezio rettangolo

Il trapezio si dice trapezio rettangolo se ha un solo lato obliquo. Nel trapezio rettangolo il primo lato DA ha la stessa misura dell'altezza CH.

Nel trapezio rettangolo i due angoli alla base maggiore non hanno la stessa misura; inoltre l'angolo DAB è un angolo retto, cioè misura 90 gradi.

Nel trapezio rettangolo i due angoli alla base minore non hanno la stessa misura; inoltre l'angolo ADC è un angolo retto, cioè misura 90 gradi.

trapezio scaleno

Il trapezio si dice trapezio scaleno se i due lati obliqui hanno lunghezza diversa.

Nel trapezio scaleno i quattro angoli interni sono tutti di diversa misura e nessuno è un angolo retto, altrimenti il trapezio sarebbe trapezio rettangolo.

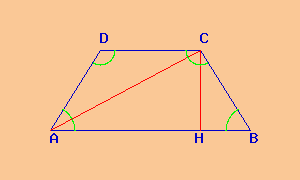
Diagonali del trapezio

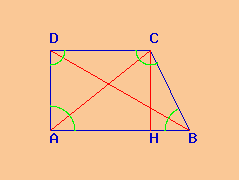
trapezio isoscele

Nel trapezio isoscele unendo due vertici opposti otteniamo le due diagonali, cioè la diagonale  AC  e la diagonale DB.

Le due diagonali hanno la stessa misura.

trapezio rettangolo

Nel trapezio rettangolo unendo due vertici opposti otteniamo le due diagonali, cioè la diagonale  AC  e la diagonale DB.

Le due diagonali non hanno la stessa misura.

Perimetro

Il perimetro del trapezio è la somma di tutti i lati, cioè la somma di base maggiore, base minore e dei due lati obliqui per il trapezio isoscele e il trapezio scaleno. Per il trapezio rettangolo il primo lato ha la stessa misura dell'altezza.

Esempio

Un trapezio isoscele ha la base maggiore di 80 cm; la base minore di 50 cm; il lato obliquo di 26 cm. Calcolare il perimetro.

Svolgimento

Dati
Poligono: trapezio ABCD
base maggiore b₁ = 80 cm
base minore b₂ = 50 cm
lato obliquo l = 26 cm

Soluzione

Si richiede il perimetro di un trapezio isoscele avente:
base maggiore b₁ = 80 cm
base minore b₂ = 50 cm
lato obliquo l = 26 cm
Per il perimetro uso la formula:
p = AB + BC + DC + AD
p = 80 cm + 26 cm + 50 cm + 26 cm = 182 cm

Risposta
Il perimetro del trapezio è 182 cm

Area del trapezio

Ricordiamo che la superficie è la parte di sopra che ricopre un trapezio, cioè tutta la parte interna del trapezio. La misura della superficie è detta area e si abbrevia con la lettera A maiuscola.

La formula dell'area vale per tutti i tipi di trapezio; ci serve la somma delle due basi e ci serve l'altezza del trapezio.

L'altezza del trapezio la indichiamo con la lettera h minuscola.

Esempio

Un trapezio isoscele ha la base maggiore di 80 cm; la base minore di 50 cm; l'altezza di 24 cm. Calcolare l'area del trapezio.

Svolgimento del problema

Mi calcolo la somma delle due basi.
Dati
base maggiore = 80 cm
base minore = 50 cm

Soluzione

Si richiede somma delle basi sapendo che:
base maggiore = 80 cm
base minore = 50 cm
Applico la formula:
somma delle basi = base maggiore + base minore
ed ottengo:
somma delle basi = 80 cm + 50 cm = 130 cm

Risposta
La somma delle basi è 130 cm



Mi calcolo l'area del trapezio.

Dati
Poligono: trapezio ABCD
somma della base maggiore b₁ + la base minore b₂ = 130 cm
altezza h = 24 cm

Soluzione
Si richiede l'area di un trapezio avente:
base maggiore b₁ + base minore b₂ = 130 cm
altezza h = 24 cm
Applico la formula:
A =


ed ottengo:
A = = 1560 cm².

Risposta

L'area del trapezio è 1560 cm².

Trapezio e teorema di Pitagora

Per la risoluzione di molti problemi è richiesta l'applicazione del teorema di Pitagora.

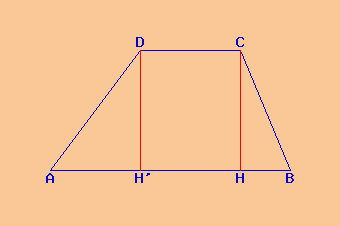
trapezio isoscele

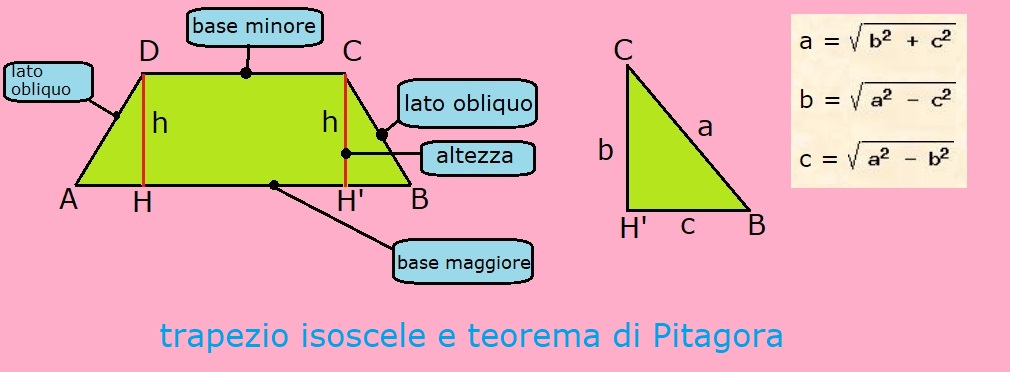
Il segmento AH si chiama proiezione del lato obliquo; esso misura nel trapezio isoscele la metà della differenza delle due basi. Il segmento AH ha la stessa misura di H'B nel trapezio isoscele.

Il triangolo H'BC è un triangolo rettangolo; l'ipotenusa del triangolo è il lato obliquo del trapezio; il cateto b del triangolo è l'altezza del trapezio; il cateto c del triangolo è il segmento H'B, che misura metà della differenza delle basi.

Esempio

Un trapezio isoscele ha l'altezza di 24 cm; la base maggiore di 80 cm; la base minore di 60 cm. Calcolare il perimetro del trapezio.

Svolgimento del problema

Ci manca la misura del lato obliquo; lo possiamo calcolare applicando il teorema di Pitagora al triangolo HBC.

Dati
Poligono: trapezio ABCD
base maggiore b₁ = 80 cm
base minore b₂ = 60 cm
altezza h = 24 cm

Soluzione

Si richiede il perimetro di un trapezio isoscele avente:
base maggiore b₁ = 80 cm
base minore b₂ = 60 cm
altezza h = 24 cm
Mi calcolo il lato obliquo con il teorema di Pitagora
BC = VAD² + ((DC-AB)/2)²
ed ottengo:
BC = V 24 ² + ((80 cm - 60 cm)/2)² = 26 cm
Per il perimetro uso la formula:
p = AB + BC +DC +AD
p = 80 cm + 60 cm + 26 cm + 26 cm = 192 cm

Risposta
Il perimetro del trapezio è 192 cm

Esempio

Un trapezio isoscele ha la base maggiore di 80 cm; la base minore di 60 cm; il lato obliquo di 26 cm. Calcolare l'area del trapezio.

Svolgimento del problema

Ci manca la misura dell'altezza; la possiamo calcolare applicando il teorema di Pitagora al triangolo HBC.

Mi calcolo prima la somma delle basi.


Dati
base maggiore = 80 cm
base minore = 60 cm

Soluzione

Si richiede somma delle basi sapendo che:
base maggiore = 80 cm
base minore = 60 cm
Applico la formula:
somma delle basi = base maggiore + base minore
ed ottengo:
somma delle basi = 80 cm + 60 cm = 140 cm

Risposta
somma delle basi è 140 cm


Dati
Poligono: trapezio isoscele ABCD
base maggiore b₁ = 80 cm
base minore b₂ = 60 cm
lato obliquo l = 26 cm

Soluzione

Si richiede l'altezza di un trapezio isoscele ABCD avente:
base maggiore b₁ = 80 cm
base minore b₂ = 60 cm
lato obliquo l = 26 cm
Mi calcolo dapprima il segmento HB dividendo a metà la differenza tra le due basi
HB = = 10 cm


Applico il teorema di Pitagora al triangolo rettangolo HBC




Dati:
Poligono: triangolo rettangolo HBC
cateto c = HB = 10 cm
ipotenusa a = BC = 26 cm

Soluzione

Si richiede un cateto di un triangolo rettangolo HBC avente:
cateto c = HB = metà differenza delle basi = 10 cm
ipotenusa a = BC = lato obliquo = 26 cm

Applico la formula derivata dal teorema di Pitagora:

cateto b = CH = altezza del trapezio = V a² - c² ed ottengo:

cateto b = V(26 cm)² - (10 cm)² = 24 cm

Risposta
L'altro cateto b = CH del triangolo rettangolo HBC, che coincide con altezza del trapezio, è 24 cm.



Dati
Poligono: trapezio ABCD
somma della base maggiore b₁ + la base minore b₂ = 140 cm
altezza h = 24 cm

Soluzione
Si richiede l'area di un trapezio avente:
base maggiore b₁ + base minore b₂ = 140 cm
altezza h = 24 cm
Applico la formula:
A =



ed ottengo:
A = = 1680 cm².

Risposta

L'area del trapezio è 1680 cm².

Esempio

Un trapezio rettangolo ha la base maggiore di 18 cm; la base minore di 10 cm; l'altezza di 24 cm. Calcola le diagonali del trapezio.

Svolgimento del problema

Dati
Poligono: trapezio rettangolo ABCD
base maggiore b₁ = 18 cm
base minore b₂= 10 cm
altezza h = 24 cm

Soluzione

Si richiedono le diagonali AC e DB di un trapezio rettangolo avente:
base maggiore b₁ = AB = 18 cm
base minore b₂ = CD = 10 cm
altezza h = CH = 24 cm

Considero il segmento AH congruente alla base minore, cioè che hanno la stessa misura.
AH = base minore = 10 cm
Per la diagonale AC applico il teorema di Pitagora al triangolo AHC




AC = V AH ² + CH ² = V 10 ² + 24 ² = 26 cm
Per la diagonale DB applico il teorema di Pitagora al triangolo ABD




DB = V DA² + AB² = V 24 ² + 18 ² = 30 cm

Risposta
La diagonale AC del trapezio rettangolo è 26 cm
La diagonale DB del trapezio rettangolo è 30 cm

prof. Pietro De Paolis

Esercizi da svolgere

Corso di matematica per scuola media

 

Lezioni matematica classe seconda	Esercizi matematica classe seconda
Lezioni classe seconda	Esercizi classe seconda
Aula classe seconda

Scuola Elettrica

 

Altre applicazioni

Mappa per tipo di scuola

 

Indice di tutte le pagine del sito

Guida per navigare

Richiesta informazioni

Scuola Elettrica