La bella geometria - Il quadrilatero

Il quadrilatero

data di oggi:

Classe 2^a della scuola media

La bella geometria

quadrilatero

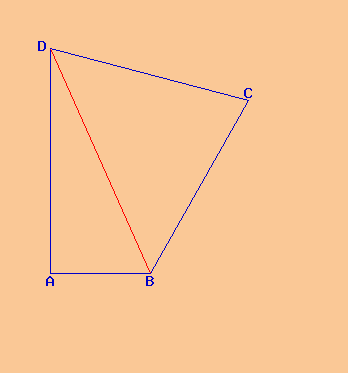
Il quadrilatero ha quattro lati tutti diversi come misura. I lati non sono paralleli, altrimenti lo chiameremmo o parallelogramma o trapezio o rettangolo o quadrato o rombo. Il quadrilatero si chiama quadrilatero in quanto ha quattro lati.

parti del quadrilatero

Unendo due vertici opposti otteniamo le due diagonali, cioè la diagonale AC e la diagonale DB.

Le due diagonali non hanno la stessa misura, altrimenti sarebbe un quadrato o un rettangolo.

Gli angoli opposti non sono uguali.

La somma degli angoli interni è 360°, cioè (4 lati - 2) x 180° = 2 x 180° = 360°.

Le due diagonali non sono tra loro ortogonali, cioè non formano un angolo di 90°, cioè un angolo retto.

Perimetro

I lati di un quadrilatero si possono sommare.

Esempio

I lati di un quadrilatero ABCD sono rispettivamente di 36 cm, 80 cm, 100 cm e 48 cm. Calcola il perimetro.

Svolgimento

Dapprima ci disegniamo un quadrilatero.

4 lati del quadrilatero

Il perimetro è la somma dei quattro lati.

Perimetro = 36 + 80 + 100 + 48 = 264 cm

La somma dei quattro lati di un quadrilatero è detta perimetro del rombo.

Il perimetro lo possiamo indicare con la lettera p minuscola.

Quindi possiamo dire:

p = 264 cm

cioè il perimetro del quadrilatero misura 264 cm.

Non esiste una formula per calcolare l'area del quadrilatero; per calcolare l'area occorre distinguere diversi tipi di quadrilatero.

quadrilatero

Osservando la figura notiamo che ogni diagonale divide il quadrilatero in due triangoli scaleni, cioè due triangoli con lati disuguali. Per cui se conosciamo i lati dei due triangoli e l'altezza dei due triangoli, ci calcoliamo le aree dei due triangoli e poi le sommiamo ottenendo l'area del quadrilatero.

Esempio

Un quadrilatero è formato da due triangoli isosceli aventi la base in comune. Calcola l'area del quadrilatero sapendo che il perimetro è 112 cm e che il lato e l'altezza relativa alla base di uno dei triangoli misurano rispettivamente 26 cm e 10 cm.

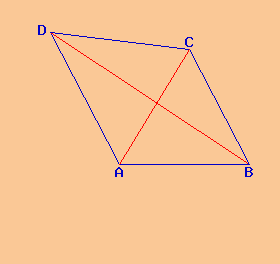
Svolgimento del problema

Si tratta di calcolare l'area dei due triangoli isosceli; di uno conosciamo il lato obliquo e l'altezza; per cui ci possiamo ricavare la base applicando il teorema di Pitagora e poi con la formula dell'area del triangolo ci possiamo calcolare l'area del primo triangolo. Del secondo triangolo isoscele conosciamo, dopo i calcoli di prima, la base in comune, per cui ci dobbiamo ricavare i due lati obliqui, dal perimetro e poi l'altezza applicando il teorema di Pitagora; e poi base per altezza e il prodotto diviso due, ci ricaviamo l'area del secondo triangolo. Poi sommiamo le due aree dei triangoli ed otteniamo quella del quadrilatero.

Ma andiamo con ordine. Ricaviamo l'altezza del primo triangolo, applicando il teorema di Pitagora.

Dati:
Poligono: triangolo rettangolo HBC
cateto b = CH = 10 cm
ipotenusa a = BC = 26 cm

Soluzione

Si richiede un cateto di un triangolo rettangolo HBC avente:
cateto b = CH = altezza = 10 cm
ipotenusa a = BC = lato obliquo del primo triangolo = 26 cm

Applico la formula derivata dal teorema di Pitagora:

cateto c = HB = metà base = V a² - b² ed ottengo:

cateto c = V(26 cm)² - (10 cm)² = 24 cm

Risposta
L'altro cateto c = HB del triangolo rettangolo HBC, che coincide con metà base, è 24 cm.

Dopo faremo il doppio ed otteniamo la base in comune ai due triangoli.

Ora vediamo di calcolare i lati obliqui del secondo triangolo, sottraendo dal perimetro i due lati obliqui del primo triangolo.

Si richiede doppio del lato del secondo triangolo sapendo che:
perimetro del quadrilatero = 112 cm
primo lato obliquo = 26 cm
secondo lato obliquo = 26 cm
Applico la formula:
doppio del lato del secondo triangolo = perimetro del quadrilatero - primo lato obliquo - secondo lato obliquo ed ottengo:
doppio del lato del secondo triangolo = 112 cm - 26 cm - 26 cm = 60 cm

Risposta
doppio del lato del secondo triangolo è 60 cm

Calcolo lato del secondo triangolo sapendo che:
doppio del lato = 60 cm
divisore = 2
Applico la formula:
lato del secondo triangolo = ed ottengo:
lato del secondo triangolo = = 30 cm

Risposta
Lato del secondo triangolo è 30 cm

Ora ci possiamo calcolare l'altezza del secondo triangolo, mediante il teorema di Pitagora.

Dati:
Poligono: triangolo rettangolo HBC
cateto c = HB = 24 cm
ipotenusa a = BC = 30 cm

Soluzione

Si richiede un cateto di un triangolo rettangolo HBC avente:
cateto c = HB = metà base = 24 cm
ipotenusa a = BC = lato obliquo del secondo triangolo = 30 cm

Applico la formula derivata dal teorema di Pitagora:

cateto b = CH = altezza del secondo triangolo = V a² - c² ed ottengo:

cateto b = V(30 cm)² - (24 cm)² = 18 cm

Risposta
L'altro cateto b = CH del triangolo rettangolo HBC, che coincide con altezza del secondo triangolo, è 18 cm.

Calcolo base in comune sapendo che:
metà base = 24 cm
rapporto = 2
Applico la formula:
base in comune = metà base x rapporto ed ottengo:
base in comune = 24 cm x 2 = 48 cm

Risposta
base in comune è 48 cm

Ci calcoliamo l'area del primo triangolo.

Dati:
Poligono: triangolo isoscele ACD
base b = AC = 48 cm
altezza h = DH = 10 cm

Soluzione
Calcolo l'area del triangolo isoscele ACD avente:
base b = AC = 48 cm
altezza h = DH = 10 cm
applico la formula A = ed ottengo:

A = = 240 cm²

Risposta
L'area del triangolo isoscele ACD è 240 cm²

Ci calcoliamo l'area del secondo triangolo.

Dati:
Poligono: triangolo isoscele ACB
base b = AC = 48 cm
altezza h = BH = 18 cm

Soluzione
Calcolo l'area del triangolo isoscele ACB avente:
base b = AC = 48 cm
altezza h = BH = 18 cm
applico la formula A = ed ottengo:

A = = 432 cm²

Risposta
L'area del triangolo isoscele ACB è 432 cm²

Ora sommiamo le due aree.
Dati
area del primo triangolo = 240 cm²
area del secondo triangolo = 432 cm²

Soluzione

Si richiede area del quadrilatero sapendo che:
area del primo triangolo = 240 cm²
area del secondo triangolo = 432 cm²
Applico la formula:
area del quadrilatero = area del primo triangolo + area del secondo triangolo
ed ottengo:
area del quadrilatero = 240 cm² + 432 cm² = 672 cm²

Risposta
area del quadrilatero è 672 cm²

Quadrilatero circoscritto

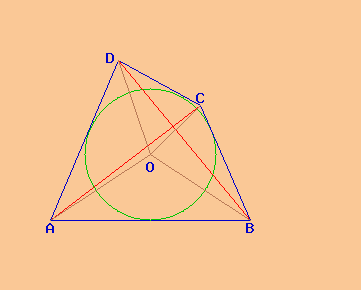
Un quadrilatero circoscritto si ha quando lo si costruisce disegnando quattro tangenti ad una circonferenza.

quadrilatero circoscritto

Nel quadrilatero circoscritto la somma dei primi due lati opposti è congruente alla somma dell'altra coppia di lati opposti. Questo è utile quando si conoscono tre lati e si vuole ricavare il quarto lato, in modo da calcolare il perimetro.

Inoltre il calcolo dell'area è più semplice in quanto si hanno quattro triangoli scaleni ma aventi tutti la stessa altezza, che è il raggio del cerchio che si trova all'interno del quadrilatero. L'altezza dei quattro triangoli si chiama anche apotema, che è un nome maschile, anche se termina con la vocale a.

In tale caso l'area del quadrilatero si calcola con la formula:
area A =

dove p è il perimetro e a è l'apotema, cioè il raggio del cerchio.

Esempio

Un quadrilatero circoscritto ad una circonferenza con il raggio di 13,2 cm, ha i lati che misurano nell'ordine 45 cm, 25 cm, 20 cm e 40 cm. Calcola il perimetro e l'area.

Svolgimento del problema

Intanto controlliamo che il quadrilatero sia circoscritto analizzando i lati; essi sono nell'ordine:

45 cm, 25 cm, 20 cm e 40 cm.

Formiamo due coppie di lati opposti, cioè una coppia tra primo lato e terzo lato; facciamo la somma dei due lati ed abbiamo:

45+20= 65 cm

Controlliamo che la somma degli altri due lati opposti sia anche 65 cm.

La coppia tra secondo lato e quarto lato ci dà come somma:

25+40= 65 cm

Quindi il quadrilatero è circoscrivibile alla circonferenza, ed è quindi quadrilatero circoscritto.

Mi calcolo prima il perimetro del quadrilatero.

Dati
primo lato = 45 cm
secondo lato = 25 cm
terzo lato = 20 cm
quarto lato = 40 cm

Soluzione

Si richiede perimetro del quadrilatero sapendo che:
primo lato = 45 cm
secondo lato = 25 cm
terzo lato = 20 cm
quarto lato = 40 cm
Applico la formula:
perimetro del quadrilatero = primo lato + secondo lato + terzo lato + quarto lato
ed ottengo:
perimetro del quadrilatero = 45 cm + 25 cm + 20 cm + 40 cm = 130 cm

Risposta
perimetro del quadrilatero è 130 cm
Ora devo applicare la formula dell'area:

A =

ricordando che l'apotema è uguale al raggio, cioè 13,2 cm.

Dati
Poligono: quadrilatero circoscritto
perimetro p = 130 cm
apotema a = raggio del cerchio inscritto = 13,2 cm

Soluzione

Si richiede l'area A di un quadrilatero avente:
perimetro p = 130 cm
apotema a = 13,2 cm
Applico la formula:
area A = ed ottengo:
area A = = 858 cm²

Risposta
L'area A del quadrilatero è 858 cm².

Quadrilatero inscritto

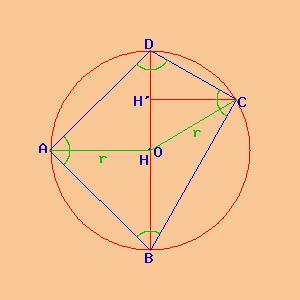
quadrilatero inscritto con una diagonale congruente con un diametro

Un quadrilatero inscritto si ha quando lo si costruisce disegnando quattro corde all'interno di una circonferenza. A volte una diagonale può coincidere con il diametro, come il caso di sopra; ma a volte non coincide con il diametro come nel disegno seguente.

quadrilatero inscritto con diagonali diverse dal diametro - trapezio isoscele

Sopra abbiamo un caso particolare, cioè un trapezio isoscele.

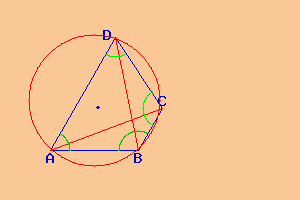
quadrilatero inscritto con diagonali diverse dal diametro

Quello di sopra non è un trapezio in quanto le due basi non sono parallele.

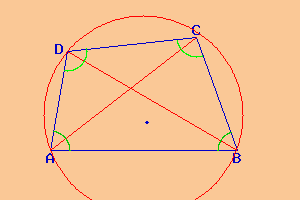
quadrilatero inscritto con una diagonale congruente con un diametro - deltoide

Quello di sopra è un deltoide, in quanto si ha la simmetria rispetto al diametro.

Per tutti i quadrilateri inscritti vale la regola degli angoli opposti; cioè la somma di due angoli opposti è pari a 180°. Inoltre, se una diagonale coincide con il diametro, il quadrilatero è la somma di due triangoli rettangoli.

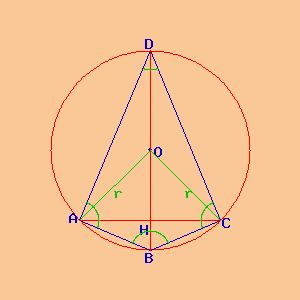
quadrilatero inscritto con una diagonale congruente con un diametro

Anche se la figura non è simmetrica rispetto al diametro, l'angolo nel vertice A è retto, cioè di 90°, in quanto il triangolo ABD è inscritto in una semicirconferenza. Anche l'angolo nel vertice C è retto, in quanto il triangolo DBC è inscritto in una semicirconferenza.

In ogni caso la somma degli angoli interni è sempre 360° per tutti i quadrilateri.

Esempio

In un quadrilatero inscritto in una circonferenza le coppie di angolo opposti sono tali che nella prima un angolo supera l'altro di 40° e nella seconda uno supera l'altro di 20°. Calcola tutti gli angoli del quadrilatero.

Svolgimento del problema

Nel quadrilatero inscritto nella circonferenza la somma degli angoli opposti è 180°.

Considero gli angoli a coppia, considerando angoli opposti.

Per esempio prima coppia formata da primo angolo e terzo angolo.

Dati
La somma di primo angolo + terzo angolo = 180 °
terzo angolo = primo angolo + 40 °
cioè
terzo angolo - primo angolo = 40 °

Soluzione
Tolgo la differenza o maggiorazione dalla somma
180 - 40 = 140 °
In 140 vi è il doppio di primo angolo.
divido per 2 ed ottengo:
primo angolo = = = 70 °

terzo angolo = primo angolo + 40 ° = 70 + 40 = 110 °

Risposta

In definitiva:
primo angolo = 70 °
terzo angolo = 110 °

Ora considero la seconda coppia di angoli opposti, cioè secondo angolo e quarto angolo.

Dati
La somma di quarto angolo + secondo angolo = 180 °
quarto angolo = secondo angolo + 20 °
cioè
quarto angolo - secondo angolo = 20 °

Soluzione
Tolgo la differenza o maggiorazione dalla somma
180 - 20 = 160 °
In 160 vi è il doppio di secondo angolo.
divido per 2 ed ottengo:
secondo angolo = = = 80 °

quarto angolo = secondo angolo + 20 ° = 80 + 20 = 100 °

Risposta

In definitiva:
secondo angolo = 80 °
quarto angolo = 100 °
In definitiva i quattro angoli misurano nell'ordine 70° - 80° - 110° 100°.

Verifico che la somma di angoli opposti sia 180°.