| data di oggi: |
Matematica utile
Le equazioni sono delle espressioni con la lettera x o y o z.
Se scrivo:
5+3=8
Si tratta di una espressione.
Se scrivo:
5+x=8
si tratta di una equazione in quanto compare la lettera x che non va confusa con il segno della moltiplicazione, cioè il per. La x indica un numero sconosciuto, cioè incognito. La lettera x si chiama incognita della equazione.
Risolvere una equazione vuol dire calcolare il valore della incognita x.
Se ho l'equazione:
5+x=8
Devo trovare un numero che sommato al 5 ci dia 8; ovviamente a mente sappiamo che il numero è 3; infatti:
5+3=8
Ma ci servono delle regole valide per tutte le equazioni.
Le equazioni ci servono per risolvere alcuni problemi nei quali conosciamo molte grandezze, cioè molti numeri, e ci manca un solo numero che non conosciamo e che vogliamo calcolare.
In realtà alcune equazioni le conosciamo da quando abbiamo studiato le proporzioni.
Esempio
Data la proporzione:
4:2=6:x
trovare il valore della incognita x.
Soluzione
Sappiamo già che x=3, ma dobbiamo sfruttare la prima proprietà fondamentale delle proporzioni, cioè:
In ogni proporzione il prodotto dei medi è uguale al prodotto degli estremi.
Considero la proporzione:
4:2=6:x
i medi sono 2 e 6; ho:
2 · 6 = 12
Gli estremi sono 4 e x; ho:
4 · x = 12
essendo il prodotto dei medi uguale al prodotto degli estremi; per trovare la x, divido per 4 primo e secondo membro ed ottengo:
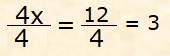
Quindi x=3 come sapevamo già.
Se, quindi, scrivo:
4 · x = 12
si tratta di una equazione in quanto compare una lettera x e altri numeri. Mentre nella proporzione i numeri sono sempre quattro, cioè due medi e due estremi, nelle equazioni i numeri possono essere molti oppure inferiori a quattro.
Diamo ora dei nomi alle parti che costituiscono una equazione.
Se ho l'equazione:
5+x=8
considero il simbolo = (uguale), si dice 1° membro dell'equazione tutti i numeri e le lettere che si trovano prima del simbolo di eguaglianza, cioè prima di =
Se ho l'equazione:
5+x=8
il 1° membro è 5+x
Si dice 2° membro dell'equazione tutti i numeri e le lettere che si trovano dopo il simbolo di eguaglianza, cioè dopo =
Se ho l'equazione:
5+x=8
il 2° membro è 8
Quindi in ogni equazione il primo membro è sempre uguale al secondo membro. Le regole di ogni equazione sono le seguenti; ogni regola si chiama principio.
1° principio di equivalenza
Il primo principio ci dice:
In ogni equazione aggiungendo uno stesso numero sia al primo membro e sia al secondo membro l'equazione non cambia, cioè resta sempre la stessa. Il numero può essere sia positivo sia negativo.
Esempio
Data l'equazione
5+x=8
aggiungo un numero a caso, per esempio 2, sia al primo membro, sia al secondo membro; ottengo:
5+x+2= 8+2
Abbiamo complicato l'equazione in quanto abbiamo scelto un numero non adatto; proviamo a scegliere un numero negativo, per esempio -5.
Data l'equazione
5+x=8
aggiungo un numero negativo -5, sia al primo membro, sia al secondo membro; ottengo:
5+x-5= 8-5
Ora sembra a prima vista più complicata, ma posso semplificare il primo membro. Il primo membro è:
5+x-5
Siccome 5-5=0
posso cancellare i due numeri e al primo membro resta solo la x; la equazione diventa:
x=8-5
Ora posso semplificare il secondo membro; il secondo membro è:
8-5
Eseguo la sottrazione:
8-5=3 e l'equazione diventa:
x=3
Ho trovato la soluzione dell'equazione:
5+x=8
la soluzione è:
x=3
Mai fidarsi dei calcoli, occorre sempre verificare, sostituendo nell'equazione originale la soluzione dell'equazione al posto della x.
Data l'equazione:
5+x=8
se al posto della x metto 3 il risultato deve essere esatto; infatti:
5+3=8
In conclusione il primo principio ci dice:
In ogni equazione, aggiungendo o sottraendo uno stesso numero sia al primo membro e sia al secondo membro, l'equazione non cambia, cioè resta sempre la stessa.
Da questo primo principio deriva una regola pratica che è questa:
Se sposto un numero dal primo membro e lo porto al secondo membro, ma lo cambio di segno, cioè da positivo a negativo, o viceversa, l'equazione non cambia.
Data l'equazione:
5+x=8
Sposto il 5 dal primo membro al secondo membro; ho:
x=8-5
da cui ottengo:
x=3
In pratica è come se avessi aggiunto -5 sia al primo membro sia al secondo membro; infatti ho:
5+x-5= 8-5
Un elemento della equazione si chiama anche termine. Anche la x è un termine.
Data l'equazione:
5=8-x
che è sempre l'equazione di prima, solo che ho spostato la x dal primo al secondo membro, cambiandola di segno. Per trovare la soluzione e quindi trovare la x, sposto dapprima il 5 da sinistra verso destra, cambiandolo di segno ed ho:
0=8-x-5
Notiamo che un membro non va lasciato vuoto; se è vuoto metto lo zero. Poi sposto -x a sinistra cambiandolo di segno; ho
x=8-5
da cui ho:
x=3
Un'altra conseguenza utile del primo principio è che se noto due termini uguali nelle somme, sia al primo sia al secondo membro, li posso eliminare tutti e due. Solo che questa regola è pericolosa. Ma proviamo.
Data l'equazione:
5+x+4=8+4
Sposto il 4 del primo membro al secondo membro, cambiandolo di segno; ottengo:
5+x=8+4-4
Semplifico il secondo membro ed ottengo:
5+x=8
E' la stessa equazione, non è cambiata. Occorre, però stare attenti ai segni e vedere se non ci siano anche dei prodotti o moltiplicazioni.
Data l'equazione:
13+x-4=8+4
non posso eliminare il 4 al primo e al secondo membro, in quanto nel primo membro il 4 è positivo e nel secondo membro è negativo.
Data l'equazione:
52+4x=60+4
Non posso eliminare il 4 in quanto nel primo membro il quattro fa parte di un prodotto, cioè 4x vuol dire che devo prendere 4 volte la variabile x; mentre al secondo membro il 4 sta da solo nella somma. Per risolverla, sposto il 52 al secondo membro e cambio di segno; ho:
4x=60+4-52
da cui:
4x=12
e qui mi fermo in quanto mi manca il secondo principio di equivalenza, cioè quello delle moltiplicazioni e delle divisioni.
2° principio di equivalenza
Il secondo principio ci dice:
In ogni equazione moltiplicando per uno stesso numero, diverso dal numero zero, sia il primo membro e sia il secondo membro l'equazione non cambia, cioè resta sempre la stessa. Il numero può essere sia positivo sia negativo.
Esempio
Data l'equazione
4x=12
Cerco un numero da moltiplicare; potrebbe essere il 4; ma se moltiplico complico le cose; ma posso scegliere anche un quarto, cioè
![]()
Questo equivale a dividere per 4 sia il primo membro sia il secondo membro; infatti il secondo principio di equivalenza va scritto in questo modo:
In ogni equazione moltiplicando o dividendo per uno stesso numero, diverso dal numero zero, sia il primo membro e sia il secondo membro, l'equazione non cambia, cioè resta sempre la stessa.
Il numero può essere sia positivo sia negativo. ma può essere anche una frazione, sia positiva sia negativa, ma sempre in entrambi i membri.
Esempio
Data l'equazione
4x=12
Cerco un numero da dividere sia il primo sia il secondo membro; mi scelgo il numero 4, in modo da semplificare subito; infatti il primo membro è 4x; divido per 4 ed ottengo x.
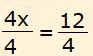
Ma devo dividere anche il secondo membro per 4; quindi ho 12:4 =3.
In conclusione ho:
x=3
Non mi fido dei calcoli, per cui verifico sempre partendo dall'equazione originale, che era:
4x=12
Al posto della x metto 3 ed ottengo:
4·3=12
Quindi non ho sbagliato.
Una conseguenza del secondo principio è che se scelgo come numero -1 la equazione cambia di segno.
Esempio
Data l'equazione:
-4x=-12
Moltiplico per il numero -1 ambo i membri ed ho:
-1(-4x)=-1(-12)
da cui:
4x=12
che ammette 3 come soluzione.
Quindi la regola è:
Se cambio di segno tutti i termini di una equazione, sia al primo membro, sia al secondo membro, l'equazione non cambia. Cambiare di segno si dice di solito moltiplicare per -1
prof. Pietro De Paolis
Corso di matematica per scuola media
|
|















