Traccia 1
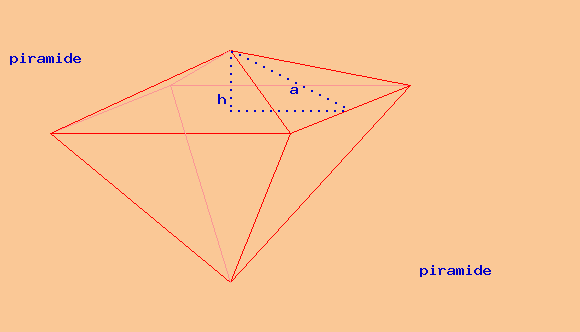
Un solido è formato da due piramidi quadrangolari con le basi coincidenti. La somma e la differenza delle altezze delle due piramidi è rispettivamente 50 cm e 14 cm. L'area della base comune è 2304 cm². Calcola l'area totale e il volume del solido. Calcola il peso sapendo che il solido è di rame.
Traccia 2
Un solido è formato da due piramidi quadrangolari con le basi coincidenti. La somma e la differenza delle altezze delle due piramidi è rispettivamente 50 cm e 14 cm. Il lato della base comune è 48 cm. Calcola l'area totale e il volume del solido.

Traccia 3
Un solido è formato da due piramidi quadrangolari con le basi coincidenti. La somma e la differenza delle altezze delle due piramidi è rispettivamente 50 cm e 14 cm. La diagonale della base comune è 67,67 cm. Calcola l'area totale e il volume del solido. Calcola il peso sapendo che il solido è di rame.

Traccia 4
Un solido è formato da due piramidi quadrangolari con le basi coincidenti. La somma e la differenza delle altezze delle due piramidi è rispettivamente 50 cm e 14 cm. L'apotema della piramide più alta è di 40 cm. Calcola l'area totale e il volume del solido.

Traccia 5
Un solido è formato da due piramidi quadrangolari con le basi coincidenti. La somma e la differenza delle altezze delle due piramidi è rispettivamente 50 cm e 14 cm. L'apotema della piramide più bassa è di 30 cm. Calcola l'area totale e il volume del solido.

Traccia 6
Un solido è formato da due piramidi quadrangolari con le basi coincidenti. La somma e la differenza delle altezze delle due piramidi è rispettivamente 50 cm e 14 cm. Il perimetro della base comune è di 192 cm. Calcola l'area totale e il volume del solido.

Traccia 7
Un solido è formato da due piramidi quadrangolari con le basi coincidenti. Le altezze delle due piramidi sono rispettivamente 18 cm e 32 cm. Il perimetro della base comune è di 192 cm. Calcola l'area totale e il volume del solido.

Traccia 8
Un solido è formato da due piramidi quadrangolari con le basi coincidenti. La somma delle altezze delle due piramidi è di 50 cm ed una è i 9/16 dell'altra. Il perimetro della base comune è di 192 cm. Calcola l'area totale e il volume del solido.

Traccia 9
Un solido è formato da due piramidi quadrangolari con le basi coincidenti. La differenza delle altezze delle due piramidi è di 14 cm ed una è i 9/16 dell'altra. Il perimetro della base comune è di 192 cm. Calcola l'area totale e il volume del solido.

Traccia 10
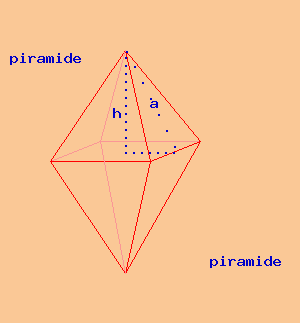
Un solido è formato da due piramidi quadrangolari con le basi coincidenti. Le due piramidi sono congruenti. L'apotema di ciascuna piramide è lungo 26 cm; la distanza tra i loro vertici è 48 cm. Calcola l'area totale e il volume del solido.
Traccia 11
Un solido è formato da due piramidi quadrangolari con le basi coincidenti. La somma delle altezze delle due piramidi è di 50 cm ed una è i 9/16 dell'altra. Lo spigolo della base comune è di 48 cm. Calcola l'area totale e il volume del solido. Il solido pesa 341,76 kg; trova la sostanza di cui è composto.

Traccia 12
Un solido è formato da due piramidi quadrangolari congruenti con le basi coincidenti. La somma delle altezze delle due piramidi è 48 cm. L'area della base comune è 400 cm². Calcola l'area totale e il volume del solido. Calcola il peso sapendo che il solido è di rame.

Traccia 13
Un solido è formato da due piramidi quadrangolari congruenti con le basi coincidenti. La somma delle altezze delle due piramidi è 48 cm. Il peso del solido è di 56,96 kg. Calcola l'area totale e il volume del solido sapendo che è di rame.

Traccia 14
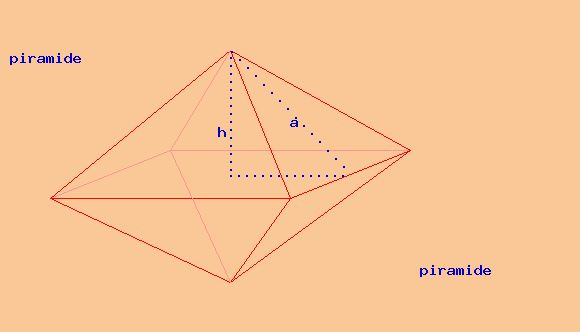
Un solido è formato da due piramidi quadrangolari con le basi coincidenti. L'area della base comune è 2304 cm². L'altezza della prima piramide è 2/3 del lato di base. L'area della superficie laterale della seconda piramide è 2880 cm². Calcola l'area totale e il peso del solido sapendo che è di rame.
Traccia 15
Un solido è formato da due piramidi quadrangolari con le basi coincidenti. L'area della superficie del solido è 6720 cm²; il perimetro della base comune è 192 cm; l'apotema di una piramide misura 40 cm. Calcola il volume del solido.

Traccia 16
Un solido è formato da due piramidi quadrangolari con le basi coincidenti. Gli apotemi delle due piramidi misurano rispettivamente 40 cm e 30 cm; l'apotema di base è lungo 24 cm. Calcola l'area totale e il volume del solido.

Traccia 17
Un solido è formato da due piramidi rette a base quadrata congruenti e con le basi coincidenti. L'area di base è di 400 cm²; l'area totale del solido è di 2080 cm². Calcola il volume del solido.

Traccia 18
Un solido è formato da due piramidi quadrangolari con le basi coincidenti. L'area della superficie del solido è 6720 cm²; il lato del quadrato della base comune è 48 cm; l'altezza di una piramide misura 32 cm. Calcola il volume del solido.

Traccia 19
Un solido è formato da due piramidi quadrangolari con le basi coincidenti. Il perimetro di base misura 192 cm. Il volume del solido è di 38400 cm³; l'altezza di una delle due piramidi è 32 cm. Calcola l'area della superficie totale del solido.

Traccia 20
Un solido è formato da due piramidi quadrangolari con le basi coincidenti. L'area di base misura 2304 cm². La somma delle due altezze è di 50 cm; l'altezza di una delle due piramidi è 9/16 di quella dell'altra. Calcola l'area della superficie totale e il volume del solido.

Traccia 21
Un solido è formato da due piramidi quadrangolari regolari aventi la base coincidente. La distanza tra i vertici delle due piramidi è 50 cm; una delle due piramidi ha l'apotema di 40 cm ed è alta 32 cm. Calcola l'area totale e il volume del solido.

Traccia 22
Un solido è formato da due piramidi rette a base quadrata congruenti e con le basi coincidenti. Lo spigolo di base è di 20 cm; il volume del solido è di 6400 cm³. Calcola l'area totale del solido.

Traccia 23
Un solido è formato da due piramidi quadrangolari con le basi coincidenti. L'area della superficie del solido è 6720 cm²; lo spigolo della base comune è 48 cm; l'apotema di una piramide misura 40 cm. Calcola il volume del solido.

Traccia 24
Un solido è formato da due piramidi rette a base quadrata congruenti e con le basi coincidenti. Lo spigolo di base è di 20 cm; l'apotema di ciascuna piramide misura 26 cm. Calcola l'area totale e il volume del solido.

Traccia 25
Un solido è formato da due piramidi rette a base quadrata congruenti e con le basi coincidenti. Lo spigolo di base è di 20 cm; l'altezza di ciascuna piramide misura 24 cm. Calcola l'area totale e il volume del solido.

Traccia 26
Un solido è formato da due piramidi rette a base quadrata congruenti e con le basi coincidenti. La distanza fra i vertici delle due piramidi è 48 cm. Lo spigolo di base comune è 5/6 dell'altezza di una piramide. Calcola l'area totale e il volume del solido.

Traccia 27
Un solido è formato da due piramidi quadrangolari con le basi coincidenti. La somma delle due altezze è di 50 cm; l'altezza di una delle due piramidi è 9/16 di quella dell'altra. Il volume della piramide più alta è di 24576 cm³. Calcola l'area della superficie totale e il volume del solido.

Traccia 28
Un solido è formato da due piramidi quadrangolari con le basi coincidenti. L'altezza di una delle due piramidi è 32 cm. L'apotema dell'altra piramide è di 30 cm. L'area della base comune è di 2304 cm². Calcola l'area della superficie totale e il volume del solido.

Traccia 29
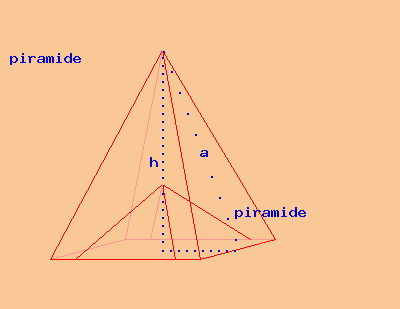
Una piramide quadrangolare regolare d'oro (ps=19,25 kg/dm³) avente lo spigolo di base e l'apotema lunghi rispettivamente 16 cm e 17 cm presenta una cavità a forma di piramide quadrangolare. Sapendo che il lato di base e l'altezza della cavità misurano rispettivamente 12 cm e 8 cm, calcola l'area della superficie totale, il volume e il peso del solido.
Traccia 30
Una piramide quadrangolare regolare presenta una cavità a forma di piramide quadrangolare avente la stessa base. L'area della base comune è di 2304 cm². La distanza tra i vertici è di 14 cm. L'apotema della piramide interna è di 30 cm. Calcola l'area della superficie totale e il volume del solido.
Traccia 31
Una piramide romboidale di rame (ps = 8,9 kg/dm³) avente le diagonali di base di 40 cm e 30 cm e l'altezza di 16 cm presenta una cavità a forma di piramide romboidale. Le diagonali della cavità sono di 20 cm e 15 cm. Il peso del solido è di 24,92 kg. Calcola l'altezza della piramide interna e l'area totale del solido.

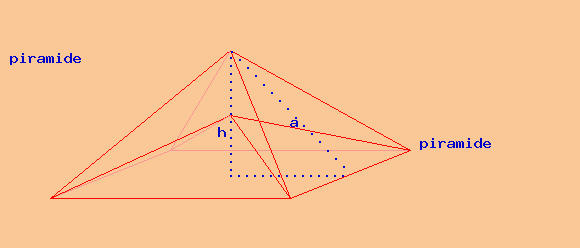
Piramide da sola
Piramide e
prisma insieme
Piramide e cono
insieme
Piramide e cilindro
insieme
Piramide e cubo
insieme
Piramide e parallelepipedo
insieme
Piramide e sfera
insieme
Attenzione
Lo
svolgimento del problema può essere sbagliato. Per la risoluzione dei problemi sul rettangolo questo programma è affidabile al
83.5 %; cioè, considerando 1400 i problemi possibili sul rettangolo, il risolutore ne risolve
1169. Considerando 700 i problemi ponibili sulla piramide, il grado di affidabilità è pari al 76.57 %, cioè risolve 536 problemi su 700.
